Kусочное представление кривых кубическими сегментами. Идея метода. Достоинства и недостатки.
Известные из теории интерполяции многочлены Лагранжа отличаются наличием осцилляций и высокой степенью при большом количестве узлов (их степень, в общем случае, N-1, где N – число узлов). Высокая степень многочлена весьма нежелательна, так как она приводит к усложнению вычислений.
На практике часто используются сплайны, т.е. кривые, составленные из сегментов, описываемых параметрически заданными многочленами третьей степени (кубическими) вида (1)  , где
, где  - независимый параметр
- независимый параметр
Часто используется нормальная параметризация, при которой значение  нормировано и принадлежит отрезку
нормировано и принадлежит отрезку  . Используется также, например, естественная параметризация, при которой значение
. Используется также, например, естественная параметризация, при которой значение  соответствует длине кривой от ее начала до точки
соответствует длине кривой от ее начала до точки  . Параметрическое представление удобно тем, что оно позволяет избежать “математических осложнений”, связанных с представлением в виде
. Параметрическое представление удобно тем, что оно позволяет избежать “математических осложнений”, связанных с представлением в виде  , например, кривых с самопересечениями. Третья степень многочлена обеспечивает удовлетворительное выполнение условий адекватной “плавности и приемлемой вычислительной трудоемкости.
, например, кривых с самопересечениями. Третья степень многочлена обеспечивает удовлетворительное выполнение условий адекватной “плавности и приемлемой вычислительной трудоемкости.
Рассмотрим, для начала, поведение одного кубического сегмента, заключенного между двумя соседними узлами интерполяции Pi(xi, yi) и Pi+1(xi+1, yi+1). Используя нормальную параметризацию, запишем условие, того, что сегмент кривой начинается в точке Pi(xi, yi) и заканчивается в точке Pi+1(xi+1, yi+1).
(2)  ;
;  ;
;  ;
;  ;
;
Очевидно, что для однозначного нахождения восьми неизвестных коэффициентов в уравнении (1) условий (2) недостаточно. Введем дополнительные условия, задав значения касательных векторов в начале и конце сегмента:
(3)  ;
;  ;
;  ;
; 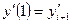 ,
,
учитывая, что
(4)  .
.
Итак, мы имеем 8 уравнений (2) и (3) и восемь неизвестных в (1). Решая систему уравнений, находим неизвестные коэффициенты в (1).
Задача интерполяции. Сплайны. Cardinal spline. Его свойства.
Задача интерполяции
Пусть функция 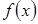 задана набором точек
задана набором точек  на интервале
на интервале  :
:
 ,
, 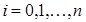 ,
,  (3.1)
(3.1)
Задача интерполяции – найти функцию  , принимающую в точках
, принимающую в точках  те же значения
те же значения  . Тогда, условие интерполяции:
. Тогда, условие интерполяции:
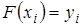 (3.2)
(3.2)
При этом предполагается, что среди значений  нет одинаковых. Точки
нет одинаковых. Точки  называют узлами интерполяции.
называют узлами интерполяции.
Если  ищется только на отрезке
ищется только на отрезке  – то это задача интерполяции, а если за пределами первоначального отрезка, то это задача экстраполяции.
– то это задача интерполяции, а если за пределами первоначального отрезка, то это задача экстраполяции.
Задача нахождения интерполяционной функции  имеет много решений, так как через заданные точки
имеет много решений, так как через заданные точки  можно провести бесконечно много кривых, каждая из которых будет графиком функции, для которой выполнены все условия интерполяции. Для практики важен случай интерполяции функции многочленами:
можно провести бесконечно много кривых, каждая из которых будет графиком функции, для которой выполнены все условия интерполяции. Для практики важен случай интерполяции функции многочленами:
 ,
,  (3.3)
(3.3)
При этом искомый полином называется интерполяционным полиномом.
При построении одного многочлена для всего рассматриваемого интервала  для нахождения коэффициентов многочлена необходимо решить систему уравнений, построенную на основе полинома (3.3). Данная система содержит
для нахождения коэффициентов многочлена необходимо решить систему уравнений, построенную на основе полинома (3.3). Данная система содержит  уравнение, следовательно, с ее помощью можно определить
уравнение, следовательно, с ее помощью можно определить  коэффициент. Поэтому максимальная степень интерполяционного многочлена
коэффициент. Поэтому максимальная степень интерполяционного многочлена  , и многочлен принимает вид
, и многочлен принимает вид
 ,
, 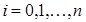 (3.4)
(3.4)
Сплайн
Сплайном называется кусочно-полиномиальная функция, определенная наотрезке [ a, b ] и имеющая на этом отрезке некоторое количество непрерывных производных. Преимущества интерполяции сплайнами по сравнению с обычными методами интерполяции – в сходимости и устойчивости вычислительного процесса.
Рассмотрим один из наиболее распространенных в практике случаев – интерполирование функции кубическим сплайном.
Пусть на отрезке [ a, b ] задана непрерывная функция  . Введем разбиение отрезка:
. Введем разбиение отрезка:
 (6)
(6)
и обозначим  ,
,  .
.
Сплайном, соответствующим данной функции  и узлам интерполяции (6) называется функция
и узлам интерполяции (6) называется функция 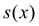 , удовлетворяющая следующим условиям:
, удовлетворяющая следующим условиям:
1) на каждом отрезке 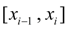 ,
,  функция
функция 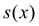 является кубическим многочленом;
является кубическим многочленом;
2) функция 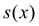 , а также ее первая и вторая производные непрерывны на отрезке [ a, b ];
, а также ее первая и вторая производные непрерывны на отрезке [ a, b ];
3) 
Третье условие называется условием интерполирования. Сплайн, определяемый условиями 1) – 3), называется интерполяционным кубическим сплайном.
Рассмотрим способ построения кубического сплайна [2].
На каждом из отрезков  ,
,  будем искать сплайн-функцию
будем искать сплайн-функцию 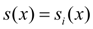 в виде полинома третьей степени:
в виде полинома третьей степени:
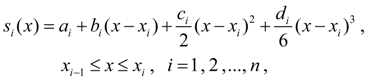 (7)
(7)
где  искомые коэффициенты.
искомые коэффициенты.
Продифференцируем (7) трижды по х:
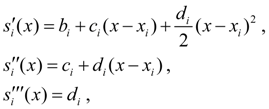
откуда следует

Из условия интерполирования 3) получаем:
 . (8)
. (8)
Кроме того, будем считать  .
.
Из условий непрерывности функции  вытекает:
вытекает:

Отсюда с учетом (7) получим:

Обозначив  и опуская промежуточные выкладки [2], окончательно получим систему уравнений для определения коэффициентов
и опуская промежуточные выкладки [2], окончательно получим систему уравнений для определения коэффициентов  :
:
 (9)
(9)
В силу трехдиагональности матрицы коэффициентов система (9) имеет единственное решение [2]. Найдя коэффициенты  , остальные коэффициенты определим по явным формулам:
, остальные коэффициенты определим по явным формулам:
 (10)
(10)
Таким образом, существует и найден единственный кубический сплайн, удовлетворяющий условиям 1) – 3).
B-сплайн

Кривые Безье.
В общем случае, кривая Безье задается векторным уравнением
(10)  , где
, где 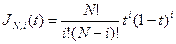 ,
,  ,
,
а  - вершины так называемого определяющего многоугольника.
- вершины так называемого определяющего многоугольника.
Кривые Безье названы в честь предложившего их французского ученого П. Безье (Bezier).
Кривые Безье обладают следующими свойствами:
1) Степень кривой N на единицу меньше числа вершин определяющего многогранника. Для двух точек кривая Безье превращается в отрезок прямой.
2) Начинается в точке  и заканчивается в точке
и заканчивается в точке  .
.
3) Вектор  сонаправлен с вектором касательной
сонаправлен с вектором касательной 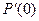 к кривой в ее начальной точке
к кривой в ее начальной точке  . Вектор
. Вектор  сонаправлен с вектором касательной
сонаправлен с вектором касательной  к кривой в ее конечной точке
к кривой в ее конечной точке  .
.
4) Целиком лежит внутри выпуклой оболочки определяющего многоугольника.
Для нас наибольший интерес представляет частный случай кривой Безье – кривая Безье третьей степени (кубическая), создаваемая по четырем точкам. При N =3 выражение (10) примет вид:
(11)  ,
,  ,
,
Кубические кривые Безье можно использовать в задачах сплайновой интерполяции для представления сегментов, если считать точки  и
и  узлами интерполяционного сплайна, а точки
узлами интерполяционного сплайна, а точки  и
и  - управляющими точками сегмента.
- управляющими точками сегмента.
Для построения цепочки кубических сегментов Безье используется метод
Graphics.DrawBeziers(Pen, Point[]). Для задания N сегментов требуется 4 + 3N точек, т.к. последняя точка любого внутреннего сегмента является первой следующего. Непрерывность касательной вдоль всего сплайна в этом методе не обеспечивается. Чтобы обеспечить непрерывность касательной, следует подбирать управляющие точки таким образом, чтобы каждый внутренний узел сплайна был серединой отрезка, соединяющего контрольную точку  предыдущего сегмента и контрольную точку
предыдущего сегмента и контрольную точку  следующего сегмента.
следующего сегмента.
NURBS кривые


Линейчатые и билинейные поврхности.
Линейчатые поверхности часто используются в авиа- и кораблестроительной промышленности. Например, большинство авиационных крыльев являются цилиндрическими линейчатыми поверхностями. Линейчатая поверхность образуется при движении прямой линии вдоль направляющей с одной степенью свободы. Другой метод определения линейчатой поверхности состоит в следующем. Выберем произвольную точку на поверхности и будем вращать вокруг нормали плоскость, проходящую через нормаль к поверхности в этой точке (см. рис. 6-27). Если существует такая ориентация плоскости, при которой каждая точка на ребре плоскости контактируют с поверхностью, то поверхность линейчата в этом направлении. Если ребро вращающейся плоскости полностью соприкасается с поверхностью при более чем одной ориентации, то поверхность в этой точке многолинейчата.
Самой простой линейчатой поверхностью является плоскость. Для квадратичных поверхностей однолинейчаты конусы и цилиндры; однополостный гиперболоид и гиперболический параболоид двулинейчаты.
В терминах отображения параметрического пространства  в объектное пространство линейчатая поверхность получается с помощью линейного интерполирования между двумя известными граничными кривыми, ассоциированными с противоположными сторонами единичного квадрата в параметрическом пространстве, скажем, между кривыми
в объектное пространство линейчатая поверхность получается с помощью линейного интерполирования между двумя известными граничными кривыми, ассоциированными с противоположными сторонами единичного квадрата в параметрическом пространстве, скажем, между кривыми  и
и 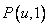 . Поверхность задается уравнениями:
. Поверхность задается уравнениями:
 (6-43)
(6-43)
или
 .
.
Заметим, что снова  и т.д., то есть концы специфированных кривых и углы поверхности совпадают. Кроме того, два края интерполированной поверхности совпадают с заданными кривыми, т.е.
и т.д., то есть концы специфированных кривых и углы поверхности совпадают. Кроме того, два края интерполированной поверхности совпадают с заданными кривыми, т.е.  и
и  .
.
Теперь предположим, что известны кривые, соответствующие  и
и  . Тогда линейчатая поверхность задается следующим образом:
. Тогда линейчатая поверхность задается следующим образом:
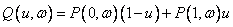 (6-44)
(6-44)
или
 .
.

Рис. 6-27 Свойства линейчатой поверхности.

Рис. 6-28 Пример линейчатой поверхности.
В этом случае опять углы поверхности совпадают с концами заданных кривых, а соответствующие края интерполированной поверхности совпадают с заданными граничными кривыми. На рис. 6-28 приводится пример линейчатой поверхности. Изображенные на этом рисунке отстоящими на некотором расстоянии от поверхности граничные кривые являются В-сплайнами третьего порядка (см. разд. 5-9). Описанная методика иллюстрируется на примере.
Пример 6-10 Линейчатая поверхность
Рассмотрим линейчатую поверхность, сформированную линейным интерполированием кривых  и и  . Найдем координаты точки . Найдем координаты точки  на поверхности с параметрами на поверхности с параметрами  . .
 является незамкнутым В-сплайном третьего порядка является незамкнутым В-сплайном третьего порядка  с определяющими вершинами ломаной, заданными точками с определяющими вершинами ломаной, заданными точками  , ,  , , 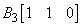 , ,  и и  (см. разд. 5-9). Отметим, что вершины (см. разд. 5-9). Отметим, что вершины  совпадают, в результате чего на кривой получается излом. совпадают, в результате чего на кривой получается излом.  также является незамкнутым В-сплайном третьей степени. Его вершины определяющей ломаной равны также является незамкнутым В-сплайном третьей степени. Его вершины определяющей ломаной равны  , ,  , ,  , ,  .
Вспоминая обсуждение В-сплайнов, получим незамкнутые однородные узловые векторы для .
Вспоминая обсуждение В-сплайнов, получим незамкнутые однородные узловые векторы для  и и  , соответственно, , соответственно,
 , ,
 .
Заметим, что ненормализованные диапазоны изменения параметров для этих двух кривых различны, .
Заметим, что ненормализованные диапазоны изменения параметров для этих двух кривых различны,  для для  и и  для для  . «Нормализованное» значение параметра линейчатой поверхности . «Нормализованное» значение параметра линейчатой поверхности  в точке в точке  соответствует соответствует  для для  и и 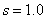 для для  .
Используя уравнения (5-83) и (5-84), получим .
Используя уравнения (5-83) и (5-84), получим

 .
В точке .
В точке  или или 


 .
Аналогичным образом .
Аналогичным образом

 .
В точке .
В точке  или или 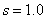
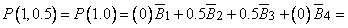

 .
Использование уравнения (6-44) для получения точки на линейчатой поверхности даст .
Использование уравнения (6-44) для получения точки на линейчатой поверхности даст
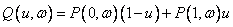 и
и


 .
Результаты показаны на рис. 6-28. Жирной точкой отмечена точка поверхности, соответствующая .
Результаты показаны на рис. 6-28. Жирной точкой отмечена точка поверхности, соответствующая  . Обратите внимание на то, что кривая . Обратите внимание на то, что кривая  , содержащая излом, плавно переходит в гладкую кривую , содержащая излом, плавно переходит в гладкую кривую  . .
|
Одной из самых простых является билинейная поверхность. Билинейная поверхность конструируется из четырех угловых точек единичного квадрата в параметрическом пространстве, т.е. из точек  ,
,  ,
,  и
и  . Любая точка на поверхности определяется линейной интерполяцией между противоположными границами единичного квадрата, как это показано на рис. 6-25. Любая точка внутри параметрического квадрата задается уравнением
. Любая точка на поверхности определяется линейной интерполяцией между противоположными границами единичного квадрата, как это показано на рис. 6-25. Любая точка внутри параметрического квадрата задается уравнением
 . (6-41)
. (6-41)
В матричном виде
 . (6-42)
. (6-42)
Необходимо, чтобы интерполируемая поверхность удовлетворяла исходным данным. В этом случае легко проверить, что угловые точки принадлежат этой поверхности, т.е.  и т.д.
и т.д.
Уравнение (6-42) задано в обобщенном матричном представлении интерполированной поверхности, а именно -матрица функций смешения по одной из бипараметрических переменных, геометрическая матрица, представляющая исходные данные, и матрица функций смешения по другой параметрической переменной.

Рис. 6-25 Билинейная интерполяция в параметрическом пространстве.
При изучении параметрических интерполированных поверхностей мы будем постоянно пользоваться этим представлением.
Если координатные векторы четырех точек, определяющих билинейную поверхность, заданы в трехмерном объектном пространстве, то будет трехмерна и билинейная поверхность, получаемая в результате отображения параметрического пространства в объектное. Если четыре определяющие точки не лежат в одной плоскости, то и билинейная поверхность также не лежит ни в какой плоскости. Действительно, в общем случае она сильно изогнута, пример этого показан на рис. 6-26. Определяющие точки являются концами противоположных диагоналей на противоположных гранях единичного куба. В результате получаем гиперболический параболоид. В качестве иллюстрации рассмотрим следующий пример.
Пример 6-9 Билинейная поверхность
Найти точку на билинейной поверхности, заданной точками 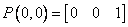 , ,  , ,  , , 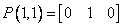 , т.е. концами противоположных диагоналей, лежащих на противоположных гранях единичного куба в объектном пространстве. Искомая точка имеет координаты , т.е. концами противоположных диагоналей, лежащих на противоположных гранях единичного куба в объектном пространстве. Искомая точка имеет координаты  в параметрическом пространстве.
Напомним, что поверхность в объектном пространстве является векторной функцией: в параметрическом пространстве.
Напомним, что поверхность в объектном пространстве является векторной функцией:
 тогда из уравнения (6-41) имеем
тогда из уравнения (6-41) имеем




 . .
 Рис. 6-26 Билинейная поверхность. (а) Определяющие угловые точки; (b) поверхность.
Рис. 6-26 Билинейная поверхность. (а) Определяющие угловые точки; (b) поверхность.
|
ПОВЕРХНОСТИ БЕЗЬЕ
Как и кривые, поверхности в компьютерной графике обычно задаются параметрически. (1)  , где
, где  и
и 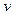 - независимые параметры.
- независимые параметры.
В матричной форме уравнение (1) записывается как
(2)  , где
, где 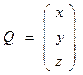 – множество точек в пространстве, образующих поверхность.
– множество точек в пространстве, образующих поверхность.
Как и в случае кривых, диапазон изменения параметров зависит от выбранного способа параметризации. При нормальной параметризации, т.е. при которой значения  и
и 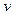 нормированы, точка с координатами (
нормированы, точка с координатами ( ;
; 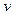 ) принадлежит единичному квадрату.
) принадлежит единичному квадрату.
 Если зафиксировать некоторое значение параметра
Если зафиксировать некоторое значение параметра 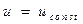 и изменять значение параметра
и изменять значение параметра 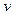 , то получится линия в пространстве, описываемая уравнением
, то получится линия в пространстве, описываемая уравнением  и называемая v -линией. Таким образом, набор фиксированных значений u порождает семейство v -линий. Аналогично определяются u -линии. Построив некоторое количество u -линий и v -линий, получим сетку топологически ортогональных параметрических кривых, каждая из которых принадлежит исходной поверхности. Параметры u и v являются внутренними криволинейными координатами на поверхности Q.
и называемая v -линией. Таким образом, набор фиксированных значений u порождает семейство v -линий. Аналогично определяются u -линии. Построив некоторое количество u -линий и v -линий, получим сетку топологически ортогональных параметрических кривых, каждая из которых принадлежит исходной поверхности. Параметры u и v являются внутренними криволинейными координатами на поверхности Q.
Поверхность Безье степени NxM задается выражением
(8)  , где
, где  ,
,  ,
,
 Для определения такой поверхность Безье требуется задать (N+1)x(M+1) точек. Чаще всего используются бикубические поверхности Безье (N=3, M=3), задаваемые 16-ю точками. Границами такого бикубического сегмента поверхности Безье являются кубические кривые Безье.
Для определения такой поверхность Безье требуется задать (N+1)x(M+1) точек. Чаще всего используются бикубические поверхности Безье (N=3, M=3), задаваемые 16-ю точками. Границами такого бикубического сегмента поверхности Безье являются кубические кривые Безье.
Подобно тому, как промежуточные управляющие точки кубической кривой задают направления касательных на ее концах, векторы  и
и  коллинеарны касательным к границам поверхности в точке
коллинеарны касательным к границам поверхности в точке  . Вектор
. Вектор  коллинеарен вектору кручения
коллинеарен вектору кручения  .
.
_____________________________________________
Бикубические поверхности Кунса предоставляют гибкое и мощное средство разработки поверхностей. Однако их практическое использование, как и для кубических сплайновых кривых, затрудняется необходимостью задания точной, интуитивно неочевидной математической информации, например координат точек, касательных векторов и векторов кручения.

Рис. 6-36 Нечетырехугольные куски. (а) Пятиугольный; (b) треугольный.
Возникающие проблемы иллюстрируются на рисунках 6-33-6-35. Большинство из этих проблем можно преодолеть, распространив понятия кривых Безье на поверхности.
Декартово или тензорное произведение поверхности Безье задается в виде
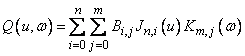 , (6-58)
, (6-58)
где  и
и  есть базисные функции Бернштейна в параметрических направлениях
есть базисные функции Бернштейна в параметрических направлениях  и
и  (см. уравнения 5-63 и 5-64). Для удобства повторим здесь определение, приведенное ранее в разд. 5-8
(см. уравнения 5-63 и 5-64). Для удобства повторим здесь определение, приведенное ранее в разд. 5-8
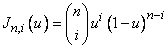 , (5-63)
, (5-63)

с
 ,
,
 . (6-64)
. (6-64)
Здесь элементы  являются вершинами задающей полигональной сетки, как это показано на рис. 6-37. Индексы
являются вершинами задающей полигональной сетки, как это показано на рис. 6-37. Индексы 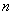 и
и  на единицу меньше числа вершин многогранника в направлениях
на единицу меньше числа вершин многогранника в направлениях  и
и  , соответственно. Для четырехсторонних кусков поверхностей задающая полигональная сетка должна быть топологически прямоугольной, т. е. должна иметь одинаковое количество вершин в каждом «ряду».
, соответственно. Для четырехсторонних кусков поверхностей задающая полигональная сетка должна быть топологически прямоугольной, т. е. должна иметь одинаковое количество вершин в каждом «ряду».
Снова, как и для кривых Безье, из-за того, что для смешивающих функций используется базис Бернштейна, многие свойства поверхности известны. Например:
Степень поверхности в каждом параметрическом направлении на единицу меньше числа вершин задающего многогранника в этом направлении.
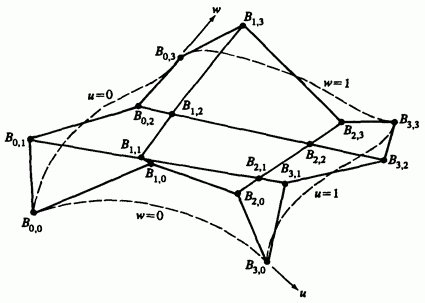
Рис. 6-37 Поверхность Безье и вершины характеристического многогранника.

Рис. 6-38 Схема задающей полигональной сетки  для поверхности Безье.
для поверхности Безье.
Гладкость поверхности в каждом параметрическом направлении на две единицы меньше числа вершин задающего многогранника в этом направлении. Поверхность отображает в общем виде форму задающей полигональной сетки. Совпадают только угловые точки задающей полигональной сетки и поверхности.
Поверхность содержится внутри выпуклой оболочки задающей полигональной сетки.
Поверхность не проявляет свойства затухания изменений. Это свойство не определено и неизвестно для поверхностей двух переменных.
Поверхность инвариантна относительно аффинного преобразования.
Каждая из граничных кривых поверхности Безье является кривой Безье. Запомним этот факт и рассмотрим задающую полигональную сетку для бикубической поверхности Безье размера  , изображенную схематично на рис. 6-38. Легко видеть, что направление и величина касательных векторов в угловых точках куска управляются положением соседних точек вдоль сторон сетки. А именно касательные векторы в направлениях
, изображенную схематично на рис. 6-38. Легко видеть, что направление и величина касательных векторов в угловых точках куска управляются положением соседних точек вдоль сторон сетки. А именно касательные векторы в направлениях  в точке
в точке  управляются вершинами полигональной сетки
управляются вершинами полигональной сетки  и
и  , соответственно. Аналогичным образом, вершины полигональной сетки
, соответственно. Аналогичным образом, вершины полигональной сетки  ,
,  ,
,  ,
,  и
и  ,
,  управляют касательными векторами в угловых точках
управляют касательными векторами в угловых точках  , соответственно. Четыре внутренние вершины полигональной сетки,
, соответственно. Четыре внутренние вершины полигональной сетки,  ,
,  ,
,  и
и  влияют на направление и величину векторов кручения в угловых точках
влияют на направление и величину векторов кручения в угловых точках  куска поверхности. Следовательно, пользователь может управлять формой куска поверхности, не зная конкретных значений касательных векторов и векторов кручения.
куска поверхности. Следовательно, пользователь может управлять формой куска поверхности, не зная конкретных значений касательных векторов и векторов кручения.
На рис. 6-39 показано несколько бикубических поверхностей Безье и их задающих полигональных сеток. Базовая полигональная сетка имеет размер  и отцентрирована относительно начала координат с угловыми точками, находящимися в
и отцентрирована относительно начала координат с угловыми точками, находящимися в  по
по  ,
,  . Компонента у угловых вершин равна нулю. У всех других вершин эта компонента равна пяти. Базовая полигональная сетка и соответствующая ей поверхность Безье изображены на рис. 6-39а. На рис. 6-39 точка
. Компонента у угловых вершин равна нулю. У всех других вершин эта компонента равна пяти. Базовая полигональная сетка и соответствующая ей поверхность Безье изображены на рис. 6-39а. На рис. 6-39 точка  является левой угловой вершиной, а
является левой угловой вершиной, а  - правой угловой вершиной. Заметим, что центральные вершины базовой полигональной сетки образуют плоский крест (показанный затененным). Следовательно, центр получившейся поверхности минимально изогнут, хотя и не плоский.
- правой угловой вершиной. Заметим, что центральные вершины базовой полигональной сетки образуют плоский крест (показанный затененным). Следовательно, центр получившейся поверхности минимально изогнут, хотя и не плоский.
На рис. 6-39b проиллюстрирован эффект увеличения в 2 раза величины касательного вектора в точке  в обоих параметрических направлениях
в обоих параметрических направлениях  и
и  с помощью перемещения точек
с помощью перемещения точек  и
и  . Вектор кручения не меняется. Отметим увеличение кривизны граничных кривых, отвечающих значениям параметров
. Вектор кручения не меняется. Отметим увеличение кривизны граничных кривых, отвечающих значениям параметров  и
и  , и соответствующее изменение внутренности поверхности.
, и соответствующее изменение внутренности поверхности.
На рис. 6-39с показано действие изменения направления касательных векторов в точке  в обоих параметрических направлениях
в обоих параметрических направлениях  и
и  с помощью перемещения точек
с помощью перемещения точек  и
и  . Отметим изменение знака кривизны граничной кривой около точки
. Отметим изменение знака кривизны граничной кривой около точки  и формы внутренней части поверхности по сравнению с базовой поверхностью.
и формы внутренней части поверхности по сравнению с базовой поверхностью.
На рис. 6-39d проиллюстрирован результат удвоения величины вектора кручения в точке  без изменения его направления. В этом случае перемещается только точка
без изменения его направления. В этом случае перемещается только точка  . Эффект этого изменения неуловим, но тем не менее важен для конструирования. Внимательное сравнение с базовой поверхностью на рис. 6-39а показывает, что параметрические линии вблизи точки
. Эффект этого изменения неуловим, но тем не менее важен для конструирования. Внимательное сравнение с базовой поверхностью на рис. 6-39а показывает, что параметрические линии вблизи точки  имеют большую кривизну. Этот эффект распространяется приблизительно до центра поверхности.
имеют большую кривизну. Этот эффект распространяется приблизительно до центра поверхности.
В матричном виде декартово произведение поверхности Безье задается выражением
 , (6-59)
, (6-59)
где
 ,
,
 ,
,
 ,
,
а матрицы 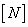 и
и  задаются уравнением (5-70) или (5-71).
задаются уравнением (5-70) или (5-71).

Рис. 6-39 Бикубические поверхности Безье. (а) Основная поверхность; (b) эффект изменения величины обоих касательных векторов в  ; (с) эффект изменения направления касательного вектора в
; (с) эффект изменения направления касательного вектора в  ; (d) эффект изменения величины вектора кручения в
; (d) эффект изменения величины вектора кручения в  .
.
Для специального случая бикубической поверхности Безье размера  уравнение (6-59) сокращается до
уравнение (6-59) сокращается до

 . (6-60)
. (6-60)
Поверхность Безье не обязательно должна быть квадратной. Для сетки размера  уравнение (6-59) превращается в
уравнение (6-59) превращается в

 . (6-61)
. (6-61)
Поверхность Безье размера  состоит из полиномиальных кривых четвертой степени в параметрическом направлении
состоит из полиномиальных кривых четвертой степени в параметрическом направлении  и из квадратичных полиномиальных кривых в направлении
и из квадратичных полиномиальных кривых в направлении  . Пример такой поверхности Безье показан на рис. 6-40. В данном случае, как это показано на рис. 6-40b, изменение центральной вершины стороны задающей сетки с пятью вершинами не влияет на касательные векторы в угловых точках.
. Пример такой поверхности Безье показан на рис. 6-40. В данном случае, как это показано на рис. 6-40b, изменение центральной вершины стороны задающей сетки с пятью вершинами не влияет на касательные векторы в угловых точках.

Рис. 6-40 Поверхность Безье размера  . (а) Основная поверхность; (b) эффект изменения центральной вершины граничной ломаной с пятью вершинами.
. (а) Основная поверхность; (b) эффект изменения центральной вершины граничной ломаной с пятью вершинами.
Производные поверхности Безье получаются с помощью формального дифференцирования уравнения (6-58) или (6-59). Если воспользоваться уравнением (6-58), то первые и вторые параметрические производные будут
 , (6-62)
, (6-62)
 , (6-63)
, (6-63)
 , (6-64)
, (6-64)
 , (6-65)
, (6-65)
 , (6-66)
, (6-66)
где штрих обозначает дифференцирование относительно параметрической переменной. Производные функций базиса Бернштейна 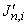 ,
,  ,
, 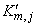 и
и  приведены в уравнениях (5-74) и (5-75).
приведены в уравнениях (5-74) и (5-75).
Легко найти соотношение между бикубическими поверхностями Безье и Кунса. Приравнивая уравнения (6-52) и (6-59), получим
 ,
,
 ,
,
где  задан уравнением (5-76) и
задан уравнением (5-76) и  - уравнением (5-70). Следовательно геометрическая матрица
- уравнением (5-70). Следовательно геометрическая матрица  бикубической поверхности Кунса задается в терминах полигональной сетки поверхности Безье следующим образом
бикубической поверхности Кунса задается в терминах полигональной сетки поверхности Безье следующим образом

или

 . (6-67)
. (6-67)
Исследование правой нижней подматрицы размера  в уравнении (6-67) подтверждает, что четыре центральные вершины задающей полигональной сетки влияют на кручение в угловых точках куска бикубической поверхности Безье. Тем не менее, кручение в угловых точках управляется не только центральными вершинами, но также и соседними касательными векторами. В самом
в уравнении (6-67) подтверждает, что четыре центральные вершины задающей полигональной сетки влияют на кручение в угловых точках куска бикубической поверхности Безье. Тем не менее, кручение в угловых точках управляется не только центральными вершинами, но также и соседними касательными векторами. В самом