Технология выполнения работы

В рамках выполнения работы необходимо составить алгоритм решения задачи в виде блок-схемы и с помощью языка псевдокода.

Содержание отчета

1. Цель работы и задание.
2. Условие задачи.
3. Алгоритм, написанный с помощью псевдокода и блок- схемы.

Вопросы для защиты работы

1. Что такое алгоритм?
2. Свойства алгоритма.
3. Способы записи алгоритма.
4. Основные элементы блок-схемы.
5. Виды алгоритмов.
6. Отличительные особенности алгоритмов с предусловием и постусловием.

Задание 1. Составить алгоритм решения задачи с помощью алгоритмического языка псевдокод и с помощью блок-схем, используя конструкцию линейного алгоритма.

1. Вычислить площадь поверхности и объем усеченного конуса по следующим формулам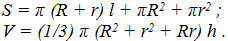

2. Вычислить координаты центра тяжести трех материальных точек с массами 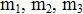и координатами

по формулам:

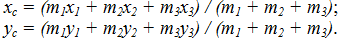
3. Вычислить площадь треугольника со сторонами a, b, c по формуле Герона:

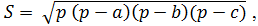
где p – полупериметр, вычисляемый по формуле (a+b+c)/2.

4. Вычислить координаты точки, делящей отрезок 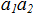в отношении 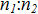по формулам:

где .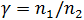

5. Вычислить медианы треугольника со сторонами a, b, c по формулам:

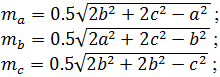
6. Вычислить площадь круга и длину окружности по введенному значению радиуса.

7. Вычислить площадь S и периметр L эллипса по введенным значениям полуосей a и b:

8. Вычислить объем V и площадь боковой поверхности цилиндра S по введенным значениям радиуса основания R и высоты цилиндра H.

9. Вычислить объем V и площадь боковой поверхности конуса S по введенным значениям радиуса основания r, высоты h и образующей l:

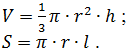
10. Вычислить объем V и площадь поверхности S сферы по введенному значению радиуса r:

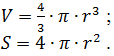
11. Дано целое четырехзначное число. Используя операции div и mod, найти сумму его цифр.

12. Дана сторона равностороннего треугольника. Найти площадь этого треугольника и радиусы вписанной и описанной окружностей.

13. Даны координаты трех вершин треугольника (x1, y1), (x2, y2), (x3, y3). Найти его периметр и площадь.

14. Дана длина окружности. Найти площадь круга, ограниченного этой окружностью.

15. Дана площадь круга. Найти длину окружности, ограничивающей этот круг.

Задание 2. Составить алгоритм решения задачи с помощью алгоритмического языка псевдокод и с помощью блок-схем, используя конструкцию алгоритма с ветвлением.

1. Составить программу для решения квадратного уравнения ax² + bx + c = 0.

2. Определить максимальное четное число из двух введенных.

3. Определить, можно ли из отрезков с длинами х, y и z построить треугольник.

4. Ввести два числа а и b. Большее число заменить утроенным произведением, меньшее – полусуммой.

5. Если среди трех чисел a, b, c имеется хотя бы одно четное, то найти максимальное число, иначе – минимальное.

6. Определить, в каком квадранте находится точка с координатами x и y и вывести номер квадранта на экран.

7. Найти квадрат наибольшего из двух чисел а и b. Вывести на экран число 1, если наибольшим является число а, число 2 – если наибольшим числом является b.

8. Определить, попадает ли точка с координатами x и y в круг радиусом R. Если точка попадает в круг, вывести на экран единицу, в противном случае – ноль.

9. Написать алгоритм решения задачи, которая решает уравнение ax + b = 0 относительно x для любых чисел a и b, введенных с клавиатуры. Все числа считаются действительными.

10. Написать алгоритм решения задачи, которая определяет, лежит ли точка А(х,у) внутри некоторого кольца («внутри» понимается в строгом смысле, т.е. случай, когда точка А лежит на границе кольца, недопустим). Центр кольца находится в начале координат. Для кольца заданы внутренний и внешний радиусы r1, r2. Координаты x и у вводятся с клавиатуры.

11. Даны две переменные целого типа: A и B. Если их значения не равны, то присвоить каждой переменной произведение этих значений, а если равны, то присвоить переменным нулевые значения.

12. Даны две переменные целого типа: A и B. Если их значения не равны, то присвоить каждой переменной минимальное из этих значений, а если равны, то присвоить переменным нулевые значения.

13. Даны целочисленные координаты точки на плоскости. Если точка не лежит на координатных осях, то вывести 0. Если точка совпадает с началом координат, то вывести 1. Если точка не совпадает с началом координат, но лежит на оси OX или OY, то вывести соответственно 2 или 3.

14. Даны вещественные координаты точки, не лежащей на координатных осях OX и OY. Вывести номер координатной четверти, в которой находится данная точка.

15. Дано целое число, лежащее в диапазоне от –999 до 999. Вывести строку – словесное описание данного числа вида "отрицательное двузначное число", "нулевое число", "положительное однозначное число" и т.д.

Задание 3. Составить алгоритм решения задачи с помощью алгоритмического языка псевдокод и с помощью блок-схем, используя конструкцию циклического алгоритма.

1. Найти сумму чисел, кратных трем, в диапазоне от 0 до 50.

2. Найти сумму первых десяти чисел, кратных пяти.

3. Найти произведение четных чисел в диапазоне от 2 до 30.

4. Вводятся положительные числа. Прекратить ввод, когда сумма введенных чисел превысит 100.

5. Требуется найти сумму чисел, кратных 7, в диапазоне от 0 до 100. Вывести на экран сумму чисел и их количество.

6. Определить количество целых чисел, кратных 3 (от 3 и далее), дающих в сумме число, превышающее 200.

7. Вводятся 10 чисел. Вывести на экран суммы положительных и отрицательных чисел и их количество.

8. Вывести на экран значения функции у=sin(x) для 0≤x≤180 c шагом в 10.

9. Подсчитать площади десяти кругов с радиусами от 1 см с шагом 2 см и вывести значения площадей на экран.

10. Вводятся положительные числа. Прекратить ввод чисел, когда их сумма превысит 100. Результат вывести на экран.

11. Вводятся числа. Прекратить ввод чисел, когда сумма положительных чисел превысит 100. Результат вывести на экран.

12. Вывести на экран значения произведений чисел a и b. Числа а изменяются от 1 до 11 с шагом 1, b – от 1 до 3 с шагом 0,2.

13. Вывести на экран таблицу перевода километров в мили в диапазоне от 2 до 20 километров с шагом 2 км.

14. Вы положили в банк 1500 рублей. Определить, сколько денег будет на Вашем вкладе через 1 год, если каждый месяц вклад увеличивается на 0.76 % от суммы предыдущего месяца.

15. Решив заняться легкой атлетикой, Вы пробежали в первый день 2 км. Сколько километров Вы пробежите за 2 недели, если каждый день Вы увеличиваете дистанцию на 10 % от предыдущего дня?