Относительные величины
Относительными статистическими величинами называют величины, выражающие количественные соотношения между социально-экономическими, правовыми явлениями или процессами. Чаще всего относительные величины представляют собой отношения двух абсолютных величин.
Величина, с которой производится сравнение (знаменатель дроби), обычно называется базой сравнения, или основанием.
В зависимости от базы сравнения относительные величины могут выражаться в виде:
1. коэффициента, если база принимается за единицу;
2. процентов (%), если база принята за 100;
3. промилле (%0), если база принята за 1000.
Выбор различных форм выражения относительных величин зависит от задачи, поставленной перед исследователем. Наиболее распространенной мерой выражения относительных величин являются проценты.
Таким образом, относительной статистической величиной называют показатель, получаемый как частное от деления одной величины на другую, характеризующий количественные соотношения между социально-экономическими, правовыми явлениями или процессами.
В статистике различают относительные величины динамики, структуры, интенсивности, сравнения и выполнения задания.
Относительные показатели динамики (ОПД) показывают изменение во времени того или иного показателя правовой статистики (числа учтенной преступности, выявленных правонарушителей, заключенных, осужденных или оправданных лиц, предъявленных исков, рассмотренных гражданских дел. штатной численности судей, прокуроров, следователей и т.д.).
Относительные показатели динамики рассчитываются как отношение уровня признака в определенном периоде или моменте времени к уровню этого же признака в предшествующем либо базисном периоде или моменте времени.
За временной период обычно принимается год (реже квартал, месяц, пятилетие). Выбор временного интервала определяется целью и характером изучения правовых явлений.
Динамика уровня преступности чаще всего представляется в абсолютных именованных единицах (числах зарегистрированных преступлений, выявленных лиц, их совершивших и т.д.) в виде статистических временных рядов по годам или другим периодам. Показатели, характеризующие динамику, перерастают в динамические ряды. При изучении развития правовых явлений и процессов для характеристики динамических рядов соответствующих совокупностей применяются:
· уровень ряда – абсолютные суммарные величины ряда;
· абсолютный прирост – разность между уровнем ряда последующего и уровнем предыдущего периода (цепной абсолютный прирост) или уровнем периода, принятого за базу (базисный абсолютный прирост);
· темп роста – отношение уровня ряда последующего периода к предыдущему (цепной темп роста) или к уровню, принятому за базу (базисный темп роста);
· темп прироста – отношение абсолютного прироста уровня последующего года к уровню предыдущего года (цепной темп прироста) или к уровню, принятому за базу (базисный темп прироста).
Темпы роста и прироста выражаются чаше всего в процентах, реже в простых отношениях, называемых коэффициентами роста
Относительными показателями структуры (ОПС) называются показатели, характеризующие долю (удельный вес) отдельных частей изучаемой совокупности в целом ее объеме.
ОПД = 
Данные показатели применяются в правовой статистике очень широко. Относительные показатели структуры рассчитывают при изучении структуры преступности (удельного веса отдельных видов или категорий преступлений), полового, возрастного и социального состава преступников, при изучении структуры гражданских исков и т.д.
Относительные показатели выполнения задания. Не смотря на проводимые реформы, планы работы остаются одним из важных аспектов управленческой деятельности органов внутренних дел, прокуратуры, судов и других юридических учреждений.
Анализ выполнения плановых мероприятий, предусмотренных в тех или иных планах и программах во всех сферах юридической деятельности, позволяет оценить степень и результативность выполнения конкретных заданий.
Относительные показатели выполнения плана (ОПВП) представляют собой отношение фактического достигнутого в конкретном периоде уровня к запланированному.
ОПВП = 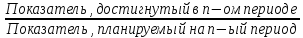
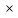 100
100
Техника расчета относительных показателей выполнения плана достаточно проста: план принимается за 100%. а фактическое его выполнение процентируется к плану.
Относительными показателями интенсивности (ОПИ) в правовой статистике называют показатели, характеризующие степень распространенности или уровень развития того или иного признака в наблюдаемой совокупности. Относительные показатели интенсивности применяются для характеристики степени распространенности гражданских споров, преступности в различных городах, регионах, странах, для отражения обеспеченности населения правоохранительными кадрами и т.д.
ОПИ = 
Относительные показатели интенсивности вычисляются путем сравнения разноименных величин, характеризующих различные явления, находящиеся между собой в определенной связи. Эти показатели, как правило, определяются в расчете на 100, 1000 и т.д. единиц показателя знаменателя (например, на 100 га земли, на 1000 человек населения и т.д.). Показатели интенсивности применяют для отражения степени развития какого-либо явления в конкретной среде.
В уголовно-правовой статистике среди относительных показателей интенсивности важное место занимает коэффициент преступности (КП). Он рассчитывается как отношение фактов преступлений или числа лиц, совершивших преступления, к численности всего населения либо к численности населения, достигшего возраста, с которого наступает уголовная ответственность.

где П – абсолютное число зарегистрированных преступлений или число лиц, их совершивших;
Н – численность всего населения или численность населения в возрасте 14 лет и старше.
Если соотнести число преступлений с численностью лиц, их совершивших, то получится коэффициент криминогенной активности преступников, показывающий, сколько преступлений в среднем совершает каждый преступник.
Относительными показателями сравнения (ОПСр) называют показатели, представляющие собой частное от деления одноименных статистических величин, характеризующих разные объекты (подразделения, районы и т.д.) и относящихся к одному и тому же периоду (или моменту) времени.

Относительные показатели сравнения исчисляются в процентах или кратных отношениях и показывают, во сколько раз одна из сравниваемых величин больше или меньше другой. Это может быть отношение как пространственного, так и временного сравнения.
Средние величины, их сущность и значение
При обработке и анализе статистического материала, кроме сравнительных данных (в виде относительных величин), часто возникает необходимость получить обобщающую характеристику уровня изучаемых явлений. Как правило, цифровое значение того или иного признака у отдельных единиц совокупности неодинаково. В этом случае требуется определить среднюю величину признака, которая давала бы обобщающую характеристику совокупности.
Средней величиной в статистике называется обобщающий показатель, который характеризует типичный уровень варьирующего признака в расчете на единицу совокупности в конкретных условиях места и времени.
Метод средних является одним из важнейших статистических методов. Основным условием правильного научного использования средней величины в статистике является качественная однородность совокупности, по которой исчислена средняя. Поэтому перед исчислением средних величин все единицы совокупности расчленяют на однородные группы, по которым и исчисляют средние. Если не произвести такого расчленения, то в результате можно прийти к «огульной» средней, которая совершенно неправильно будет характеризовать наблюдаемую совокупность.
В статистике применяются различные виды средних величин: средняя арифметическая, средняя гармоническая, средняя геометрическая, а также структурные средние – мода, медиана и др.
Наиболее распространенным видом средних величин в статистике является средняя арифметическая, представляющая собой частное от деления суммы индивидуальных значений признаков на их количество.
Средняя арифметическая является наиболее распространенным видом средних величин. Она бывает двух видов: средняя арифметическая простая и средняя арифметическая взвешенная.Средняя арифметическая простая есть частное от деления суммы величин на их число. Средняя арифметическая взвешенная применяется в тех случаях, когда значения признаков повторяются по нескольку раз. Например, в городском ОВД по 12 уголовных дел в месяц рассматривает не один, а 10 следователей, по 10 уголовных дел - 18 следователей по 18 дел - 5 и по 8 дел - 7 следователей. Иными словами, средняя арифметическая взвешенная есть частное от деления суммы произведений каждого значения признака на число единиц имеющих это значение, - на общее число единиц совокупности.Иногда значение признака выражается не в виде определенного числа, а виде интервала «от - до».В этом случае необходимо сначала определить центры интервалов (как среднюю арифметическую интервала), а потом производить расчеты.