Кафедра РТиС
Отчет
По лабораторной работе №2
На тему: «Изучение электромагнитного поля в круглом и коаксиальном волноводах»
По дисциплине «ФиТСЧ»
Выполнили студенты:
группы ИТС – 31
Данилов В.О.
Жало А.Е.
Швецов Д.В.
______________________
(подпись, дата)
Проверил:
к.т.н., доцент Павлов В.В
______________________
(подпись, дата)
Йошкар-Ола
Цель работы: изучить структуру поля волны основного типа в круглом волноводе и волны Т-типа и коаксильном волноводе, методы измерения параметров волн с помощью измерительной линии. Изучить поведение электромагнитных волн в волноводе вблизи критической частоты.
Теоретическая часть
1.1 Круглый металлический волновод представляет собой круглую трубу с внутренним 2а, на концах которого располагают фланцы для соединения волноводов друг с другом или переходы на волноводы другого сечения. Как и в прямоугольном, в круглом волноводе могут распространяться волны электрического и магнитного типов, но структура поля в нем иная. В соответствии с формой волновода электромагнитное поле в нем имеет цилиндрическую симметрию и проще описывается в цилиндрической системе координат ρ,φ,z. Зависимость полей от ρ описывается цилиндрическими функциями Бесселя или первой производной от них, а от угла – синусом или косинусом. О распределении фаз в продольном направлении можно судить, исследуя суперпозицию падающих и отраженных волн. Если существует лишь падающая волна (волновод нагружен на согласованную нагрузку), то амплитуда электрической и магнитной составляющих во всех сечениях одинакова. Если нагрузка отличается от согласованной, то появляется отраженная волна. Складывая падающую и отраженную волну, можно получить полное поле в волноводе. Амплитуда электрического или магнитного поля в каждом сечении зависит от разности фаз в обеих волнах и изменяется от сечения к сечению. На этом явлении основываются методы измерения длины волны в волноводе. Это же явление определяет величину КСВ, характеризующую согласованность элементов в СВЧ тракте и самого тракта с нагрузкой. Ниже описывается методика, позволяющая значительно уменьшить ошибку измерения больших КСВ.
Как прямоугольные, так и круглые волноводы чаще используют на частотах выше критической. При подходе сверху к частоте критической для существующего в волноводе типа колебания, резко возрастают потери и волновое сопротивление. Теоретически на критической частоте эти величины бесконечны для волновода без потерь, а в волноводе с потерями потери велики, но конечны. На частотах ниже критической, колебательный процесс экспоненциально затухает с расстоянием и волновод можно использовать как запредельный аттенюатор.
Если частота меньше критической, то длина волны в волноводе 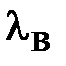 становиться мнимой, а значит, волновое число
становиться мнимой, а значит, волновое число 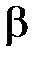 и волновое сопротивление
и волновое сопротивление 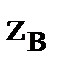 тоже будет мнимым. Чтобы избавиться от этой мнимости, введем величину k следующим равенством:
тоже будет мнимым. Чтобы избавиться от этой мнимости, введем величину k следующим равенством: 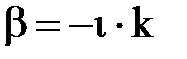 , Распределение электрического поля вдоль волновода описывается экспоненциально затухающей функцией:
, Распределение электрического поля вдоль волновода описывается экспоненциально затухающей функцией: 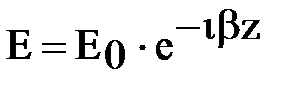 . На частотах ниже критической колебательный процесс переходит в апериодический.
. На частотах ниже критической колебательный процесс переходит в апериодический.
Иная картина наблюдается в том случае, если учесть потери, которые всегда присутствуют. Тогда плоская волна затухает:
 .
.
На частотах выше критической длина волны становится комплексной
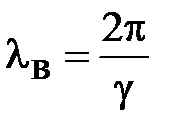 . На частотах ниже критической
. На частотах ниже критической  в знаменателе под корнем получиться
в знаменателе под корнем получиться
1.1. Лабораторная установка
Лабораторная установка имеет многофункциональное назначение и модифицируется в процессе выполнения лабораторной работы. В качестве источника используется генератор Г4-123 (2). СВЧ энергия от генератора подводится к коаксиальной измерительной линии 4 с помощью кабеля 3.
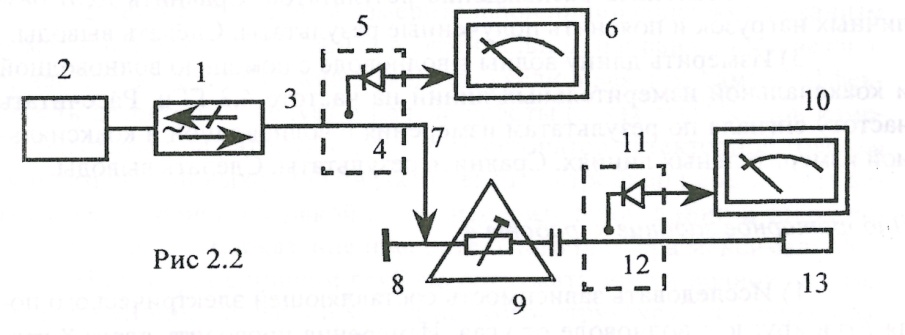
На выход измерительной линии могут подключаться различные нагрузки. На рис 2.2 подключен коаксиальный кабель 7, соединяющий коаксиальную линию с переходом 8 на волноводный тракт. Аттенюатор 9 служит для исследования распределения электрического поля по углу в круглом волноводе. На выходе аттенюатора установлена измерительная линия 12, изготовленная из отрезка прямоугольного волновода. В качестве нагрузки 13 используется либо согласованная нагрузка, либо короткое замыкание. Сигналы с измерительных линий 4 и 12 детектируются детекторами 5 и 11 и подаются на измерительные приборы 6 и 10.
Практическая часть
Лабораторное задание к работе 3
2.1. Измерим длину волны в коаксиальной измерительной линии на четырех частотах в диапазоне 3…4 ГГц. Воспользовавшись полученным значением для длины волны, рассчитаем частоту колебаний в каждом случае.
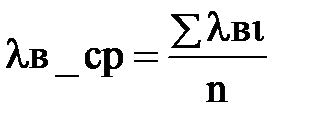
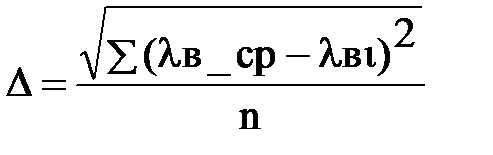
f1=3200МГц
| Zmin1 мм | Zmax1 мм | Zmin2 мм | Zmax2 мм | 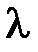 1=2(Zmin2-Zmin1)
мм 1=2(Zmin2-Zmin1)
мм
| 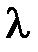 2=2(Zmax2-Zmax1)
мм 2=2(Zmax2-Zmax1)
мм
| 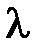 3=4(Zmin1-Zmax1)
мм 3=4(Zmin1-Zmax1)
мм
|
| 52,45 | 77,80 | 98,70 | 120,10 | 92,50 | 84,60 | 101,40 |
| 53,35 | 75,65 | 99,35 | 123,15 | 92,00 | 95,00 | 89,20 |
| 53,80 | 76,20 | 98,40 | 121,95 | 89,20 | 91,50 | 89,60 |
| 53,05 | 76,40 | 98,80 | 122,20 | 91,50 | 91,60 | 93,40 |
| 52,10 | 76,35 | 99,50 | 124,90 | 94,80 | 97,10 | 97,00 |
| лв_ср | 92,00 | 91,96 | 94,12 | |||
| ∆ | 0,80 | 1,90 | 2,06 |
f2=3350 МГц
| Zmin1 мм | Zmax1 мм | Zmin2 мм | Zmax2 мм | 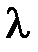 1=2(Zmin2-Zmin1)
мм 1=2(Zmin2-Zmin1)
мм
| 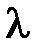 2=2(Zmax2-Zmax1)
мм 2=2(Zmax2-Zmax1)
мм
| 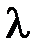 3=4(Zmin1-Zmax1)
мм 3=4(Zmin1-Zmax1)
мм
|
| 74,60 | 96,75 | 117,80 | 143,20 | 86,40 | 92,90 | 88,60 |
| 74,95 | 99,55 | 118,15 | 139,80 | 86,40 | 80,50 | 98,40 |
| 75,10 | 99,60 | 118,05 | 141,25 | 85,90 | 83,30 | 98,00 |
| 74,70 | 98,75 | 119,30 | 143,90 | 89,20 | 90,30 | 96,20 |
| 73,75 | 98,95 | 117,90 | 143,55 | 88,30 | 89,20 | 100,80 |
| лв_ср | 87,24 | 87,24 | 96,40 | |||
| ∆ | 0,57 | 2,06 | 1,86 |
f2=3500 МГц
| Zmin1 мм | Zmax1 мм | Zmin2 мм | Zmax2 мм | 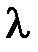 1=2(Zmin2-Zmin1)
мм 1=2(Zmin2-Zmin1)
мм
| 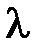 2=2(Zmax2-Zmax1)
мм 2=2(Zmax2-Zmax1)
мм
|  3=4(Zmin1-Zmax1)
мм 3=4(Zmin1-Zmax1)
мм
|
| 59,80 | 83,05 | 103,95 | 124,80 | 88,30 | 83,50 | 93,00 |
| 59,35 | 81,10 | 103,75 | 125,15 | 88,80 | 88,10 | 87,00 |
| 60,25 | 83,75 | 103,80 | 124,05 | 87,10 | 80,60 | 94,00 |
| 59,05 | 82,15 | 104,90 | 124,55 | 91,70 | 84,80 | 92,40 |
| 61,05 | 81,70 | 103,25 | 125,20 | 84,40 | 87,00 | 82,60 |
| лв_ср | 88,06 | 84,80 | 89,80 | |||
| ∆ | 1,06 | 1,18 | 1,94 |
f2=3650 МГц
| Zmin1 мм | Zmax1 мм | Zmin2 мм | Zmax2 мм | 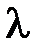 1=2(Zmin2-Zmin1)
мм 1=2(Zmin2-Zmin1)
мм
| 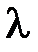 2=2(Zmax2-Zmax1)
мм 2=2(Zmax2-Zmax1)
мм
| 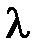 3=4(Zmin1-Zmax1)
мм 3=4(Zmin1-Zmax1)
мм
|
| 73,10 | 94,65 | 114,95 | 134,95 | 83,70 | 80,60 | 86,20 |
| 72,45 | 93,05 | 114,25 | 134,90 | 83,60 | 83,70 | 82,40 |
| 73,80 | 93,65 | 114,70 | 134,80 | 81,80 | 82,30 | 79,40 |
| 74,05 | 95,55 | 113,35 | 133,50 | 78,60 | 75,90 | 86,00 |
| 73,55 | 93,80 | 114,10 | 134,45 | 81,10 | 81,30 | 81,00 |
| лв_ср | 81,76 | 80,76 | 83,00 | |||
| ∆ | 0,84 | 1,18 | 1,21 |
2.2. Измерим КСВ открытого конца волновода, согласованной нагрузки и входного сопротивления коаксиального кабеля, подключенного к волноводному переходу
2.2.1. Измерение КСВ входа коаксиального кабеля
f1=3200МГц
1 способ: Umax= 173,45 мВ; Umin=149,1 мВ
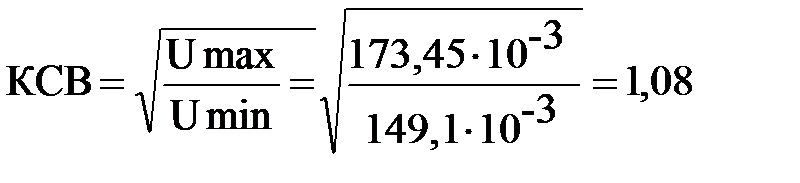
2 способ:
Umin=149,1 мВ; Z1=146,35 мм; Umax= 173,45 мВ; Z2= 151,9 мм
S=Z2-Z1=151,9-146,35=5,55
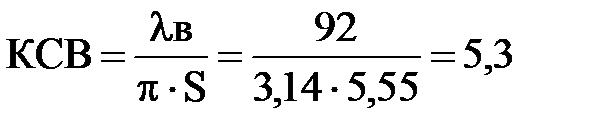
2.2.2. Измерение КСВ открытого конца
1 способ: Umax= 155,15 мВ; Umin=130,95 мВ
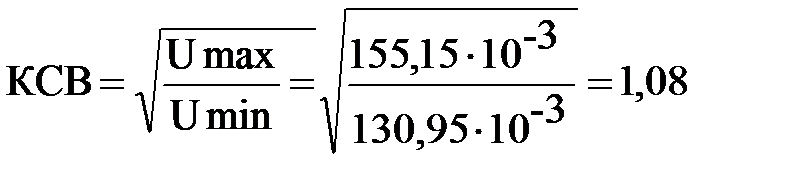
2 способ:
Z1=130.15 мм, Z2= 131.6 мм,
S=Z2-Z1=131.6-130.15=1.45
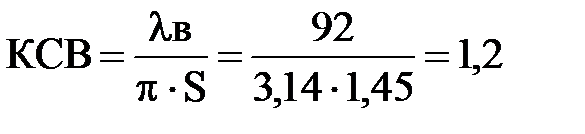
2.2.3. Измерение КСВ согласованной нагрузки
Umax= 126,75 мВ; Umin=99,75 мВ
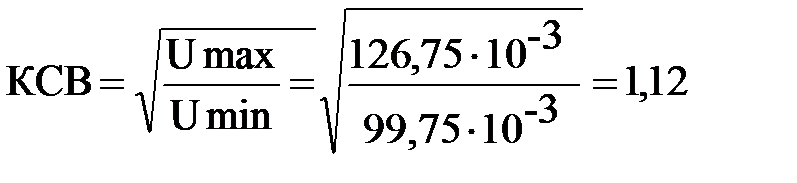
2.3. Измерим длину волны в волноводной измерительной линии на частоте f=4300 МГц
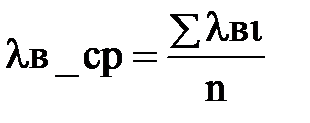
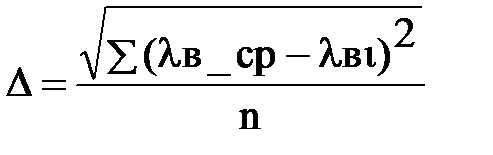
2.3.1. Измерение длины волны с помощью волноводной измерительной линии
| Zmin1 мм | Zmax1 мм | Zmin2 мм | Zmax2 мм | 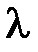 1=2(Zmin2-Zmin1)
мм 1=2(Zmin2-Zmin1)
мм
|  2=2(Zmax2-Zmax1)
мм 2=2(Zmax2-Zmax1)
мм
|  3=4(Zmin1-Zmax1)
мм 3=4(Zmin1-Zmax1)
мм
|
| 59,42 | 85,41 | 110,45 | 133,20 | 102,06 | 95,58 | 103,96 |
| 58,74 | 84,02 | 112,80 | 132,73 | 108,12 | 97,42 | 101,12 |
| 60,75 | 84,01 | 109,77 | 132,71 | 98,04 | 97,40 | 93,04 |
| 58,11 | 82,87 | 108,90 | 133,23 | 101,58 | 100,72 | 99,04 |
| 61,85 | 82,99 | 114,10 | 134,64 | 104,50 | 103,30 | 84,56 |
| лв_ср | 102,86 | 98,88 | 96,34 | |||
| ∆ | 1,49 | 1,24 | 3,08 |
2.3.2. Измерение длины волны с помощью коаксиальной измерительной линии
| Zmin1 мм | Zmax1 мм | Zmin2 мм | Zmax2 мм | 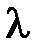 1=2(Zmin2-Zmin1)
мм 1=2(Zmin2-Zmin1)
мм
| 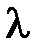 2=2(Zmax2-Zmax1)
мм 2=2(Zmax2-Zmax1)
мм
| 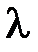 3=4(Zmin1-Zmax1)
мм 3=4(Zmin1-Zmax1)
мм
|
| 82,35 | 100,35 | 118,05 | 135,25 | 71,40 | 69,80 | 72,00 |
| 83,20 | 100,55 | 116,90 | 135,60 | 67,40 | 70,10 | 69,40 |
| 82,20 | 101,90 | 116,55 | 134,80 | 68,70 | 65,80 | 78,80 |
| 83,30 | 100,60 | 118,15 | 136,10 | 69,70 | 71,00 | 69,20 |
| 81,90 | 100,45 | 118,20 | 134,10 | 72,60 | 67,30 | 74,20 |
| лв_ср | 69,96 | 68,80 | 72,72 | |||
| ∆ | 0,83 | 0,87 | 1,59 |
 69 мм
69 мм
2.4. Исследование распределения по углу электрического поля в круглом волноводе
Построим пронормированную на единицу теоретическую кривую зависимости электрического поля от угла в круглом волноводе (2.4.1)
| α,град | U изм,мкВ | Pизм(α),мкВт | Pп(α) | е(α) |
| 0,44 | ||||
| 0,76 | ||||
| 0,88 | ||||
| 420,5 | 1,13 | |||
| 1,40 | ||||
| 1,59 | ||||
| 1,77 | ||||
| 1,87 | ||||
| 1,92 | ||||
| 4,5 | 1,95 |
Посчитаем мощность потерь:
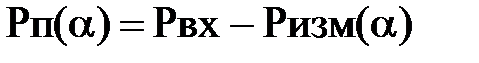

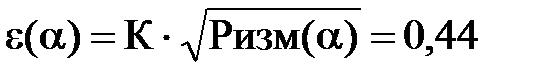
Рис.2.4.1. Зависимость электрического поля от угла в круглом волноводе
2.5. Исследуем зависимость и амплитуды электрического поля в волноводе вблизи критической частоты. Построим экспериментальные точки рис 2.5.1
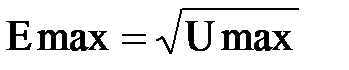
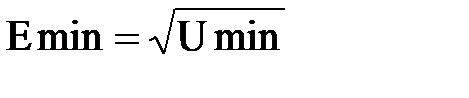
Найдём амплитуду электрического поля
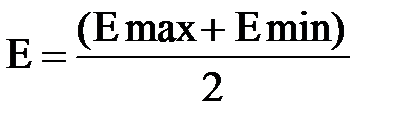
| f,МГц | Umin,мкВ | Umax,мкВ | Emin,мВ | Emax,мВ | E,мВ |
| 16,50 | 22,00 | 4,06 | 4,69 | 4,38 | |
| 10,00 | 12,40 | 3,16 | 3,52 | 3,34 | |
| 7,50 | 9,20 | 2,74 | 3,03 | 2,89 | |
| 29,30 | 30,50 | 5,41 | 5,52 | 5,47 | |
| 20,00 | 28,00 | 4,47 | 5,29 | 4,88 | |
| 15,10 | 21,50 | 3,89 | 4,64 | 4,26 | |
| 55,00 | 68,40 | 7,42 | 8,27 | 7,84 | |
| 19,50 | 21,20 | 4,42 | 4,60 | 4,51 | |
| 16,00 | 20,80 | 4,00 | 4,56 | 4,28 | |
| 18,00 | 20,50 | 4,24 | 4,53 | 4,39 | |
| 22,00 | 28,50 | 4,69 | 5,34 | 5,01 | |
| 22,50 | 29,30 | 4,74 | 5,41 | 5,08 | |
| 31,50 | 37,00 | 5,61 | 6,08 | 5,85 |
Рис.2.5.1.Экспериментальные точки
Рассчитаем теоретически зависимость электрического поля на выходе волноводной системы от частоты
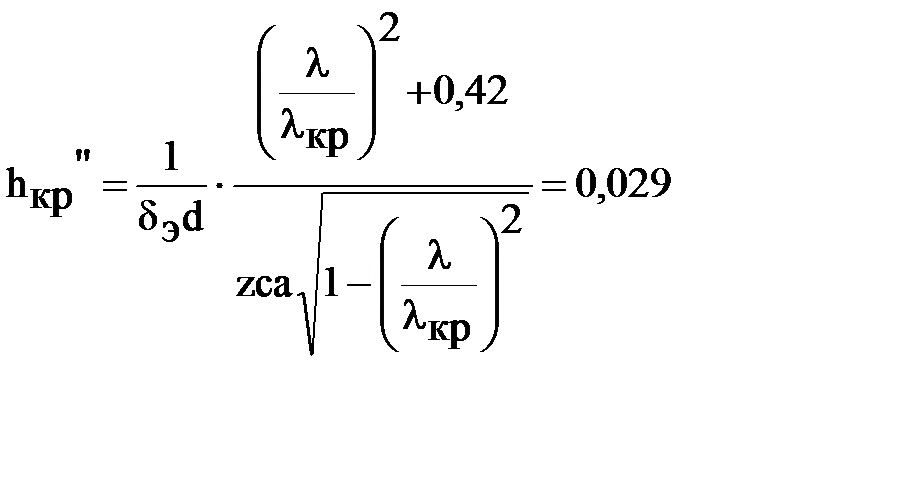


Вывод: изучили структуру поля волны основного типа в круглом волноводе и волны Т-типа и коаксиальном волноводе, методы измерения параметров волн с помощью измерительной линии. Изучили поведение электромагнитных волн в волноводе вблизи критической частоты. Измерили длину волны в коаксиальной измерительной линии на четырех частотах в диапазоне3…4ГГц. Измерили 3 вида КСВ входа коаксиального кабеля, открытого конца, согласованной нагрузки, 1 способ: КСВ=1,08, 2 способ: КСВ=5,3, КСВ входа коаксиального кабеля отличаются, это значит, что 2 способ не походит. Исследование распределения по углу электрического поля в круглом волноводе. Построили пронормированную на единицу теоретическую кривую зависимости электрического поля от угла в круглом волноводе, которая с увеличением угла стремится к 0. Исследовали зависимость и амплитуды электрического поля в волноводе вблизи критической частоты. Рассчитали теоретически зависимость электрического поля на выходе волноводной системы от частоты Рвых=179,4 мВт.