Полярные координаты на плоскости.
 ЗАДАНИЕ N 1 сообщить об ошибке
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Полярные координаты на плоскости
Точка  задана в прямоугольной системе координат. Тогда ее полярные координаты равны …
задана в прямоугольной системе координат. Тогда ее полярные координаты равны …

|  
| ||
 
| |||
 
| |||
 
|
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Полярные координаты на плоскости
В полярной системе координат дана точка  Тогда расстояние от нее до полярной оси равно …
Тогда расстояние от нее до полярной оси равно …

| |||
Решение:
Расстояние от точки M до полярной оси определяется длиной перпендикуляра, опущенного из нее на ось. Рассмотрим прямоугольный треугольник AOM, где O – полюс, A – основание перпендикуляра. Тогда длина перпендикуляра MA будет равна: 
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Полярные координаты на плоскости
В полярной системе координат даны точки  и
и  Тогда расстояние между ними равно …
Тогда расстояние между ними равно …

| |||
Решение:
Рассмотрим треугольник AOB, где O – полюс. По теореме косинусов получим:  где
где  Тогда
Тогда 
 ЗАДАНИЕ N 30 сообщить об ошибке
ЗАДАНИЕ N 30 сообщить об ошибке
Тема: Полярные координаты на плоскости
В полярной системе координат заданы две точки  и
и  Тогда расстояние между ними равно …
Тогда расстояние между ними равно …

| |||

| |||

| |||
Решение:
Точки  и
и  лежат на одной прямой и отстоят от полюса на расстояния 2 и 7 соответственно. Следовательно, длина образованного ими отрезка
лежат на одной прямой и отстоят от полюса на расстояния 2 и 7 соответственно. Следовательно, длина образованного ими отрезка 
 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Полярные координаты на плоскости
В полярной системе координат даны две смежные вершины квадрата  и
и  Тогда длина диагонали квадрата равна …
Тогда длина диагонали квадрата равна …

| |||
Решение:
Диагональ квадрата можно вычислить по формуле  Так как треугольник AOB – прямоугольный
Так как треугольник AOB – прямоугольный  где O – полюс, то
где O – полюс, то  Тогда
Тогда 
 ЗАДАНИЕ N 28 сообщить об ошибке
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Полярные координаты на плоскости
В полярной системе координат даны две точки  и
и  Тогда полярные координаты середины отрезка AB равны …
Тогда полярные координаты середины отрезка AB равны …

| 
| ||

| |||

| |||

|
 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Полярные координаты на плоскости
Полярные координаты точки, симметричной точке  относительно полярной оси, равны …
относительно полярной оси, равны …

| 
| ||

| |||

| |||

|
Решение:
Полярные координаты  точки, симметричной точке
точки, симметричной точке  относительно полярной оси, отличаются полярным углом и запишутся в виде
относительно полярной оси, отличаются полярным углом и запишутся в виде  или
или 
 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Полярные координаты на плоскости
Уравнение окружности с центром в начале координат радиуса 5 в полярных координатах имеет вид …

| 
| ||

| |||

| |||

|
Решение:
Уравнение окружности с центром в начале координат радиуса a в прямоугольных декартовых координатах имеет вид  Подставим вместо x и y их значения по формулам перехода от декартовых координат к полярным:
Подставим вместо x и y их значения по формулам перехода от декартовых координат к полярным:  . Получим:
. Получим: 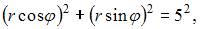 или
или 
 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Полярные координаты на плоскости
Одна из вершин треугольника находится в полюсе O, две другие имеют координаты  и
и  Тогда площадь треугольника AOB равна …
Тогда площадь треугольника AOB равна …

| 
| ||

| |||
Решение:
Площадь треугольника можно вычислить по формуле  где
где  – угол между сторонами OA и OB. Тогда
– угол между сторонами OA и OB. Тогда 
Прямая на плоскости.
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Прямая на плоскости
Угловой коэффициент прямой, проходящей через точки  и
и  равен …
равен …

| |||

| |||
| – 19 | |||

|
Решение:
Прямая, проходящая через две данные точки  и
и  задается уравнением вида:
задается уравнением вида:  Тогда
Тогда  или
или  Угловой коэффициент данной прямой равен
Угловой коэффициент данной прямой равен 
 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Прямая на плоскости
В треугольнике с вершинами 

 уравнение высоты, проведенной из вершины C, имеет вид …
уравнение высоты, проведенной из вершины C, имеет вид …

| 
| ||

| |||

| |||

|
Решение:
Воспользуемся уравнением прямой, проходящей через точку  перпендикулярно нормальному вектору
перпендикулярно нормальному вектору 
 В качестве нормального вектора возьмем вектор
В качестве нормального вектора возьмем вектор  а в качестве заданной точки возьмем точку
а в качестве заданной точки возьмем точку  Тогда
Тогда  или
или 
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Прямая на плоскости
Прямые  и
и  пересекаются в точке, лежащей на оси абсцисс. Тогда эта точка имеет координаты …
пересекаются в точке, лежащей на оси абсцисс. Тогда эта точка имеет координаты …

| 
| ||

| |||

| |||

|
Решение:
Точка, лежащая на оси абсцисс, имеет координаты  Подставим координаты этой точки в уравнения прямых:
Подставим координаты этой точки в уравнения прямых: 



 . Тогда
. Тогда 
 ЗАДАНИЕ N 29 сообщить об ошибке
ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Прямая на плоскости
Уравнение прямой, проходящей через точку пересечения прямых  и
и  перпендикулярно прямой
перпендикулярно прямой  имеет вид …
имеет вид …

| 
| ||

| |||

| |||

|
Решение:
Уравнение прямой, перпендикулярной прямой  можно определить как
можно определить как  , где для определения
, где для определения  найдем точку пересечения прямых
найдем точку пересечения прямых  и
и  :
:


Подставим в уравнение прямой  координаты точки
координаты точки  :
:  , отсюда
, отсюда  Тогда уравнение искомой прямой примет вид
Тогда уравнение искомой прямой примет вид  .
.
 ЗАДАНИЕ N 21 сообщить об ошибке
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Прямая на плоскости
Прямая проходит через точку  перпендикулярно прямой
перпендикулярно прямой  Тогда общее уравнение этой прямой имеет вид …
Тогда общее уравнение этой прямой имеет вид …

| 
| ||

| |||

| |||

|
Решение:
Перепишем уравнение прямой 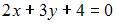 в виде
в виде 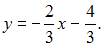 Угловые коэффициенты перпендикулярных прямых связаны соотношением
Угловые коэффициенты перпендикулярных прямых связаны соотношением 
Тогда угловой коэффициент искомой прямой равен  а уравнение прямой будет иметь вид
а уравнение прямой будет иметь вид  Параметр b найдем из условия
Параметр b найдем из условия 
 Тогда
Тогда  или
или 
 ЗАДАНИЕ N 29 сообщить об ошибке
ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Прямая на плоскости
Длина перпендикуляра, опущенного из начала координат на прямую, заданную уравнением  равна …
равна …

| |||
Решение:
Применим формулу  для вычисления расстояния d от точки
для вычисления расстояния d от точки  до прямой
до прямой  Тогда
Тогда 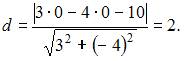
 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Прямая на плоскости
Расстояние между прямыми  и
и  равно …
равно …

| 2,5 | ||
| 0,25 | |||
| 1,5 |
Решение:
Расстояние между двумя прямыми найдем как расстояние между прямой  и точкой прямой
и точкой прямой  например,
например,  Применим формулу
Применим формулу  для вычисления расстояния d от точки
для вычисления расстояния d от точки  до прямой
до прямой  Тогда
Тогда 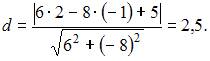
 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Прямая на плоскости
Площадь треугольника, образованного пересечением прямой  с осями координат, равна …
с осями координат, равна …

| |||
Решение:
Приведем уравнение прямой l к уравнению прямой «в отрезках»:  или
или  Уравнение прямой «в отрезках», отсекающей на координатных осях Ox и Oy отрезки длиной a и b соответственно, имеет вид:
Уравнение прямой «в отрезках», отсекающей на координатных осях Ox и Oy отрезки длиной a и b соответственно, имеет вид:  Следовательно, треугольник, образованный прямой l и осями координат – прямоугольный, с вершинами
Следовательно, треугольник, образованный прямой l и осями координат – прямоугольный, с вершинами 

 и гипотенузой AB. Площадь треугольника AOB будет равна:
и гипотенузой AB. Площадь треугольника AOB будет равна: 
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Прямая на плоскости
Прямая задана в параметрическом виде 
Тогда ее общее уравнение имеет вид …

| 
| ||

| |||

| |||

|
Решение:
Общее уравнение прямой на плоскости записывается в виде  Выразив из системы уравнений
Выразив из системы уравнений  параметр t как
параметр t как  и
и  получаем:
получаем:  или
или 
Кривые второго порядка.
 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Кривые второго порядка
Радиус окружности  равен …
равен …

| |||

| |||

|
Решение:
Окружность радиуса R с центром в точке  задается на плоскости уравнением вида
задается на плоскости уравнением вида  Выделим в уравнении
Выделим в уравнении  полные квадраты:
полные квадраты:
 или
или 
Тогда радиус окружности равен 2.
 ЗАДАНИЕ N 27 сообщить об ошибке
ЗАДАНИЕ N 27 сообщить об ошибке
Тема: Кривые второго порядка
Точки  и
и  являются концами одного из диаметров окружности. Тогда уравнение окружности имеет вид …
являются концами одного из диаметров окружности. Тогда уравнение окружности имеет вид …

| 
| ||

| |||

| |||

|
Решение:
Окружность радиуса R с центром в точке  задается на плоскости уравнением
задается на плоскости уравнением  Центр окружности имеет координаты середины отрезка AB:
Центр окружности имеет координаты середины отрезка AB: 
 Радиус окружности равен
Радиус окружности равен  Тогда уравнение окружности примет вид
Тогда уравнение окружности примет вид 
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Кривые второго порядка
Уравнением кривой второго порядка  на плоскости определяется …
на плоскости определяется …

| эллипс | ||
| гипербола | |||
| парабола | |||
| пара пересекающихся прямых |
Решение:
Выделим в уравнении  полный квадрат по переменной x:
полный квадрат по переменной x:  или
или  Разделив обе части этого уравнения на 10, получим уравнение вида:
Разделив обе части этого уравнения на 10, получим уравнение вида:  которое на плоскости определяет эллипс.
которое на плоскости определяет эллипс.
 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Кривые второго порядка
Эллипсы  и
и  пересекаются в точках с абсциссой, равной …
пересекаются в точках с абсциссой, равной …

| |||
Решение:
Координаты точек пересечения эллипсов найдем из решения системы  . Умножив первое уравнение на 36, второе – на 45, получим
. Умножив первое уравнение на 36, второе – на 45, получим  . Вычтем из первого уравнения второе:
. Вычтем из первого уравнения второе:  Отсюда
Отсюда 
 ЗАДАНИЕ N 25 сообщить об ошибке
ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Кривые второго порядка
Расстояние между фокусами гиперболы  равно …
равно …

| |||
| 2,5 |
Решение:
Фокусы гиперболы, заданной каноническим уравнением  имеют координаты
имеют координаты  и
и  где
где  Тогда
Тогда  То есть расстояние между двумя точками
То есть расстояние между двумя точками  и
и  равно 10.
равно 10.
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Кривые второго порядка
Вершина параболы  имеет координаты …
имеет координаты …

| 
| ||

| |||

| |||

|
Решение:
Выделим в уравнении  полный квадрат:
полный квадрат: 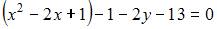 или
или  Тогда вершина параболы имеет координаты
Тогда вершина параболы имеет координаты 
 ЗАДАНИЕ N 30 сообщить об ошибке
ЗАДАНИЕ N 30 сообщить об ошибке
Тема: Кривые второго порядка
Уравнение директрисы параболы, проходящей через точки 
 и симметричной относительно оси Ox, имеет вид …
и симметричной относительно оси Ox, имеет вид …

| 
| ||

| |||

| |||

|
Решение:
Каноническое уравнение параболы, проходящей через начало координат и симметричной относительно оси Ox имеет вид:  а уравнение директрисы:
а уравнение директрисы:  Параметр p находится из условия, что точка
Параметр p находится из условия, что точка  принадлежит параболе, то есть
принадлежит параболе, то есть 
 Тогда уравнение директрисы параболы примет вид:
Тогда уравнение директрисы параболы примет вид: 
 ЗАДАНИЕ N 25 сообщить об ошибке
ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Кривые второго порядка
Соотношение  в прямоугольной декартовой системе координат задает …
в прямоугольной декартовой системе координат задает …

| параболу | ||
| гиперболу | |||
| эллипс | |||
| окружность |
Решение:
Вычислим  то есть
то есть 
Тогда в прямоугольной декартовой системе координат данное уравнение задает параболу с вершиной в точке 
Плоскость в пространстве.
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Плоскость в пространстве
Уравнение плоскости, проходящей через точки  и
и  параллельно вектору
параллельно вектору  имеет вид …
имеет вид …

| 
| ||

| |||

| |||

|
Решение:
Рассмотрим некоторую точку  принадлежащую искомой плоскости. Необходимо, чтобы вектора
принадлежащую искомой плоскости. Необходимо, чтобы вектора 
 и
и  были компланарны. То есть уравнение плоскости, проходящей через точки
были компланарны. То есть уравнение плоскости, проходящей через точки  и
и  параллельно вектору
параллельно вектору  , может быть представлено в следующем виде:
, может быть представлено в следующем виде: 
Тогда  или
или 
Следовательно, уравнение плоскости примет вид:

 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Плоскость в пространстве
Уравнение плоскости, проходящей через точку  параллельно векторам
параллельно векторам  и
и 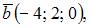 имеет вид …
имеет вид …

| 
| ||

| |||

| |||

|
Решение:
Уравнение плоскости, проходящей через точку  с нормальным вектором
с нормальным вектором  имеет вид:
имеет вид:  В качестве нормального вектора плоскости возьмем векторное произведение векторов
В качестве нормального вектора плоскости возьмем векторное произведение векторов  и
и 
Тогда  или
или 
Подставляя в уравнение плоскости координаты точки  и вектора
и вектора  получим:
получим:  или
или 
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Плоскость в пространстве
Плоскости  и
и  перпендикулярны при значении m, равном …
перпендикулярны при значении m, равном …

| 
| ||

| |||

| |||

|
Решение:
Плоскости, заданные общими уравнениями  и
и  перпендикулярны при условии, что
перпендикулярны при условии, что 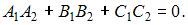 Тогда
Тогда  то есть
то есть 
 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Плоскость в пространстве
Общее уравнение плоскости, проходящей через точку  параллельно плоскости
параллельно плоскости  имеет вид …
имеет вид …

| 
| ||

| |||

| |||

|
Решение:
Уравнение плоскости, параллельной плоскости  имеет вид:
имеет вид:  Подставим координаты точки
Подставим координаты точки  в это уравнение:
в это уравнение:  Тогда
Тогда 
 ЗАДАНИЕ N 28 сообщить об ошибке
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Плоскость в пространстве
Уравнение плоскости, проходящей через точку 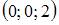 перпендикулярно плоскостям
перпендикулярно плоскостям  и
и  имеет вид …
имеет вид …

| 
| ||

| |||

| |||

|
Решение:
Уравнение плоскости, проходящей через точку  с нормальным вектором
с нормальным вектором  имеет вид:
имеет вид:  В качестве нормального вектора плоскости возьмем векторное произведение нормальных векторов плоскостей
В качестве нормального вектора плоскости возьмем векторное произведение нормальных векторов плоскостей  и
и 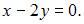 Тогда
Тогда  или
или  Подставляя в уравнение плоскости координаты точки
Подставляя в уравнение плоскости координаты точки  и вектора
и вектора  получим:
получим:  или
или 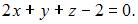
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Плоскость в пространстве
Общее уравнение плоскости, проходящей через точку  и отсекающей равные отрезки на координатных осях, имеет вид …
и отсекающей равные отрезки на координатных осях, имеет вид …

| 
| |||||
Поиск по сайту©2015-2025 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2017-12-29 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |