ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
В урну, в которой лежат 6 белых и 5 черных шаров добавляют два черных шара. После этого наудачу по одному извлекают три шара без возвращения. Тогда вероятность того, что хотя бы один шар будет белым, равна …

| 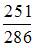
| ||

| |||

| |||

|
Решение:
Введем обозначения событий: Ak – k – ый вынутый шар будет белым, A – хотя бы один шар будет белым. Тогда  где
где 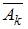 – k – ый вынутый шар не будет белым. Так как по условию задачи события
– k – ый вынутый шар не будет белым. Так как по условию задачи события 
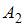 и
и 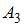 зависимы, то
зависимы, то

 ЗАДАНИЕ N 1 сообщить об ошибке
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
В урну, в которой лежат 6 белых и 5 черных шаров добавляют два белых шара. После этого наудачу по одному извлекают три шара без возвращения. Тогда вероятность того, что все три шара будут белыми, равна …

| 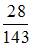
| ||

| |||
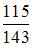
| |||

|
Решение:
Введем обозначения событий: Ak – k – ый вынутый шар будет белым, A – все три шара будут белыми. Тогда  и так как по условию задачи события
и так как по условию задачи события 
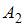 и
и 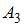 зависимы, то
зависимы, то
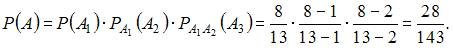
 ЗАДАНИЕ N 38 сообщить об ошибке
ЗАДАНИЕ N 38 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
Из урны, в которой лежат 3 белых и 7 черных шара, наудачу по одному извлекают два шара без возвращения. Тогда вероятность того, что только один из извлеченных шаров будет белым, равна …

| 
| ||

| |||

| |||
|
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
В электрическую цепь последовательно включены два элемента, работающие независимо друг от друга. Вероятности отказов элементов равны соответственно 0,1 и 0,15. Тогда вероятность того, что тока в цепи не будет, равна …

| 0,235 | ||
| 0,765 | |||
| 0,22 | |||
| 0,015 |
Решение:
Введем обозначения событий: Ak (откажет k – ый элемент), A (тока в цепи не будет).
Тогда
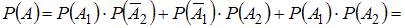

 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
В электрическую цепь последовательно включены три элемента, работающие независимо друг от друга. Вероятности отказов элементов равны соответственно 0,1, 0,2 и 0,15. Тогда вероятность того, что тока в цепи не будет, равна …

| 0,388 | ||
| 0,612 | |||
| 0,45 | |||
| 0,003 |
Решение:
Введем обозначения событий: Ak (откажет k – ый элемент), A (тока в цепи не будет, то есть откажет хотя бы один элемент).
Тогда

 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
В электрическую цепь параллельно включены три элемента, работающие независимо друг от друга. Вероятности отказов элементов равны соответственно 0,05, 0,1 и 0,20. Тогда вероятность того, что тока в цепи не будет, равна …

| 0,001 | ||
| 0,35 | |||
| 0,999 | |||
| 0,01 |
Решение:
Введем обозначения событий: Ak (откажет k – ый элемент), A (тока в цепи не будет).
Тогда

 ЗАДАНИЕ N 38 сообщить об ошибке
ЗАДАНИЕ N 38 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
Наладчик обслуживает три станка. Вероятность того, что в течение часа потребует его вмешательства первый станок, равна  ; второй –
; второй – 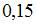 ; третий –
; третий –  . Тогда вероятность того, что в течение часа потребует вмешательства наладчика только один станок, равна …
. Тогда вероятность того, что в течение часа потребует вмешательства наладчика только один станок, равна …

| 0,329 | ||
| 0,1 | |||
| 0,45 | |||
| 0,003 |
Решение:
Введем обозначения событий: Ak (вмешательства наладчика потребует k – ый станок), A (вмешательства наладчика потребует только один станок).
Тогда

Учитывая, что  получаем
получаем

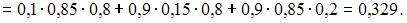
 ЗАДАНИЕ N 35 сообщить об ошибке
ЗАДАНИЕ N 35 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
Студент знает ответы на 15 из 20 вопросов программы. Тогда вероятность того, что студент ответит на один из двух предложенных ему вопросов, равна …

| 
| ||

| |||

| |||
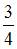
|
Решение:
Введем обозначения событий: Ak (студент знает ответ на k – ый предложенный ему вопрос), A (студент знает ответы на один из двух предложенных ему вопросов).
Тогда 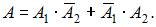 А так как по условию задачи события
А так как по условию задачи события 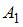 и
и 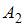 зависимы, то
зависимы, то

 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
Студент знает ответы на 15 из 20 вопросов программы. Тогда вероятность того, что студент ответит на все три предложенных ему вопроса, равна …

| 
| ||
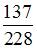
| |||
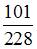
| |||

|
Решение:
Введем обозначения событий: Ak (студент знает ответ на k – ый предложенный ему вопрос), A (студент знает ответы на все три предложенных ему вопроса).
Тогда 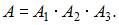 А так как по условию задачи события
А так как по условию задачи события 
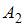 и
и 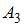 зависимы, то
зависимы, то

 ЗАДАНИЕ N 37 сообщить об ошибке
ЗАДАНИЕ N 37 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
Экзаменационный билет содержит три вопроса. Вероятность того, что студент ответит на первый вопрос, равна 0,8, на второй – 0,9, на третий – 0,7. Тогда вероятность того, что студент ответит на все три вопроса, равна …

| 0,504 | ||
| 0,8 | |||
| 0,576 | |||
| 0,496 |
Решение:
Введем обозначения событий: Ak (студент знает ответ на k – ый вопрос), A (студент ответит на все три вопроса).
Тогда
 и
и