Основные физические механизмы теплообмена. Теплоотдача. Температурное поле, температурный градиент. Теплопроводность.

1. Температурное поле, температурный градиент.

Теплоперенос – это самопроизвольный необратимый процесс переноса теплоты, обусловленный неоднородным температурным полем.

Температурное поле – это совокупность мгновенных значений температуры во всех точках тела в данный момент времени:

(1)

Здесь t – температура, ⁰ С; x,y,z – координаты точки, τ – момент времени, с.

Уравнение (1) описывает нестационарное температурное поле. Если , то температурное поле является стационарным:

(2).

В неоднородном температурном поле можно выделить ряд изотермических поверхностей, т.е. поверхностей с одинаковой температурой, изменяющейся при переходе от одной поверхности к другой. Характер этого изменения, т.е. степень неоднородности температурного поля, может быть определен понятием градиента температуры.

Выделим в теле две изотермические поверхности с бесконечно малой разностью температур Δt. Выберем некоторую точку О на одной поверхности и определим направление нормали n к поверхности в этой точке. Направление нормали определяет кратчайшее расстояние между поверхностями и является направлением наибольшего изменения температуры. Градиентом температуры называют вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной от температуры по этому направлению. Если - единичный вектор в направлении нормали, то . В декартовой системе координат вектор градиента может быть записан в виде:

(3).

1. Основные физические механизмы теплообмена.

Теплопроводностью называют теплообмен, при котором перенос энергии в форме теплоты в неравномерно нагретой среде имеет атомно-молекулярный характер и не связан с макроскопическим движением среды. В этом случае в газах перенос энергии осуществляется молекулами, в металлах – в основном, электронами проводимости, в диэлектриках – за счет связанных колебаний частиц.

Конвективный теплоперенос – это перенос теплоты вместе с переносом массы, т.е. в неравномерно нагретой жидкой, газообразной или сыпучей среде.

Лучистый теплообмен – это теплообмен между телами, происходящий за счет испускания и поглощения ими электромагнитного излучения.

3. Теплопроводность.

3.1 Основной закон теплопроводности Фурье

Опытным путем установлен следующий основной закон теплопроводности:

количество теплоты dQ, проходящее через элемент изотермической поверхности dS за промежуток времени dτ, пропорционально градиенту температуры:

(4).

Величина , равная количеству теплоты, проходящему через элемент поверхности dS в единицу времени, называется тепловым потоком и имеет размерность Дж/с, или Вт. Плотностью теплового потока называется тепловой поток через единицу поверхности: , имеет размерность Вт/м².

Поскольку это величина векторная, и направление теплового потока противоположно направлению градиента температуры, то в векторной форме

(5)

– это уравнение обычно называют основным законом теплопроводности Фурье.

Коэффициент пропорциональности λ в уравнениях (4), (5) есть теплофизическая характеристика материала, называемая коэффициентом теплопроводности. В зависимости от величины λ материалы могут быть хорошими или плохими проводниками тепла, а также теплоизоляторами. К хорошим проводникам тепла относятся металлы, к плохим – диэлектрики и газы, к теплоизоляторам ­– пористые материалы.

Наряду с теплопереносом вводится понятие теплоотдача – это теплообмен между поверхностью твердого тела и соприкасающейся с ней средой – теплоносителем (жидкостью, газом). Основной закон теплоотдачи – закон Ньютона-Рихмана

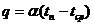(6),

где - температура поверхности тела, - температура теплоносителя, α – коэффициент теплоотдачи, размерность α – Вт/(м²К).

3.2 Дифференциальное уравнение теплопроводности.

Уравнения (4) - (5) дают возможность определить плотность теплового потока и количество теплоты, проходящее через заданную поверхность в заданный промежуток времени при известном температурном поле. Для нахождения температурного поля t(x,y,z,τ) служит дифференциальное уравнение теплопроводности. Оно выводится на основе первого закона термодинамики – закона сохранения энергии в тепловых процессах. Опуская вывод, запишем это уравнение в виде:

(7)

Здесь с – массовая удельная теплоемкость материала, ρ – его плотность, q_v- плотность распределенных в теле источников тепла (если таковые имеются),
. С учетом основного закона теплопроводности Фурье

уравнение (7) может быть переписано в виде

(8).

Если коэффициент теплопроводности считать константой, то его можно вынести из под знака div, и тогда, с учетом (3) окончательный вид уравнения теплопроводности будет:

(9).

В простых задачах чаще всего внутренние источники тепла в теле отсутствуют, т.е. q_v=0. Тогда уравнение (9) обычно используют в виде:

(10),

где величина называется температуропроводностью, размерность – м²/с. Эта теплофизическая характеристика определяет скорость изменения температурного поля в данном материале. При высоких значениях a распределение температуры в теле изменяется быстро, при низких – медленно.

3.2.1 Условия однозначности

Уравнения (8) –(10) являются уравнениями для решения краевых задач математической физики. Они могут быть решены только для конкретной постановки задачи, которая включает в себя следующие условия:

-геометрические (размеры, форма, уравнение поверхности, ограничивающей тело);

-физические (все теплофизические характеристики материала тела и его плотность);

-начальные (распределение температуры в теле как функция координат в начальный момент времени: );

-граничные условия (на поверхности, ограничивающей тело, как функция времени).

Остановимся отдельно на граничных условиях (ГУ). Они могут быть заданы несколькими способами.

1. ГУ I рода подразумевают задание температуры на поверхности тела в виде функции времени: t(x,y,z)_пов=f(τ).

2. ГУ II рода подразумевают задание на поверхности тела плотности теплового потока: q (x,y,z)_пов=q_c(τ).

3. ГУ III рода записываются в виде уравнения Ньютона-Рихмана, задающего закон теплообмена между поверхностью тела и окружающей средой:

q (x,y,z)_пов= .

Стационарные задачи теплопроводности.

Стационарным называется установившийся режим, при котором температурное поле не меняется со временем. Тогда дифференциальное уравнение теплопроводности превращается в .

Проще всего получить аналитическое решение в простой одномерной геометрии, например, плоская стенка, размеры которой по двум направлениям (y,z) намного превышают размер в направлении х (толщина стенки). Легко представить себе стенку гаража или дома, отделяющую внутреннюю среду от внешней. Тогда по высоте и ширине стенки температура практически не меняется, а для изменения ее по толщине остается уравнение

(11)

Оно может быть решено для любого типа граничных условий при задании толщины стенки, теплопроводности ее материала и коэффициента теплоотдачи (для ГУ III рода).

Рассмотрим решение для ГУ I рода, т.е. на одной поверхности (х=0) задана температура t₁, на другой (x=L) – температура t₂. Общее решение имеет вид:

(12),

что сразу говорит о линейном распределении температуры в плоской стенке.

Константы находим, подставляя в (12) последовательно граничные условия на обеих поверхностях. В результате зависимость температуры от координаты приобретает вид:

(13).

Определим плотность теплового потока через плоскую стенку:

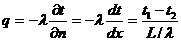(14).

Как видим, плотность теплового потока в плоской стенке не зависит от координаты, она постоянна в любом сечении стенки. Величина разности температур на поверхностях стенки называется полным температурным напором, а отношение L/λ – термическим сопротивлением стенки. Уравнение (14) наводит на аналогии с электрическим током: температурный напор – эквивалент падения напряжения на концах проводника, термическое сопротивление – эквивалент электрического сопротивления, плотность теплового потока – эквивалент электрического тока, а (14) – эквивалент закона Ома. Этими аналогиями удобно пользоваться при решении практических задач.

Полученное решение легко обобщается на случай многослойной стенки, если по прежнему заданы ГУ I рода. Термическое сопротивление многослойной стенки равно сумме термических сопротивлений составляющих ее слоев:

(15).

Плотность теплового потока через такую стенку равна

(16),

а температуры на стыках слоев могут быть получены путем последовательной записи уравнения (14) для каждого из слоев, начиная с первого, при этом q уже известна (для плоской стенки величина плотности теплового потока одинакова в любом сечении!), а единственное неизвестное – температура на границе со следующим слоем.

Интересен случай теплопередачи через плоскую стенку, разделяющую две среды: с одной стороны поверхности стенки заданы t_cp1 и коэффициент теплоотдачи α₁, с другой – t_cp2 и коэффициент теплоотдачи α₂ (заданы ГУ

III рода)_. Запишем последовательно выражения для плотности теплового потока на одной поверхности, внутри стенки и на другой поверхности:

Преобразуем выписанные уравнения так, чтобы в их правых частях остались только разности температур, после чего сложим почленно левые и правые части уравнений. Получим:

,

откуда получаем плотность теплового потока

(17).

Если продолжить электрическую аналогию, то в этом случае термическое сопротивление стенки изменилось: к нему добавились термические сопротивления на теплоотдающих поверхностях: 1/α₁, 1/α₂. Для этого случая величина, обратная термическому сопротивлению, называется коэффициентом теплопередачи К, так что q = K(t_cp1-t_cp2).

3.2.4 Нестационарные задачи теплопроводности.

В общем случае зависящего от времени температурного поля требуется решать уравнения (9) или (10) одним из доступных методов – аналитическим или численным. Аналитическое решение можно получить только для простых геометрий: неограниченной плоской стенки, бесконечно длинного цилиндра или шара. В более сложных случаях применяют различные численные методы: метод конечных разностей (МКР), интегро-дифференциальный метод (метод баланса), метод конечных элементов (МКЭ). МКЭ используется во многих современных программных комплексах.