КОНЕЧНЫЕ ГРУППЫ С ПОЧТИ БОЛЬШИМ НЕПРИВОДИМЫМ ХАРАКТЕРОМ

 

	Выполнила: студентка 3 курса группы МО-15 ИМИ СВФУ Никитина Анжелика Ариановна Руководитель работы: ПоисееваСаргылана Семеновна, старший преподаватель кафедры алгебры и геометрии ИМИ СВФУ
Работа проверена ___ ______________ 2018 г. Оценка __________________ _________________ С.С. Поисеева

 

Якутск – 2018

СОДЕРЖАНИЕ

Введение..……………………..………………………………….………………… 3

1 Теория конечных групп…………………………………………………………. 5

1.1 Силовские p -подгруппы………….…………………………………......…. 5

1.2 Простые группы ………………………………………………………...…..13

2 Теория представлений групп ….………………………………………...............18

2.1 Представления группы…….………………………………………………..18

2.2 Характеры группы.………………………………………………………… 20

3. Практическая часть.……………………………………………………….…… 23

3.1 Краткая характеристика, история и возможности системы GAP.………23

3.2 Конечные группы с почти большим неприводимым характером …...… 26

Заключение ……………………………………………………………………….. 30

Список использованной литературы……………..……………………………...31

 

 

ВВЕДЕНИЕ

 

Теория групп является наиболее важным, перспективным и интенсивно развивающимся направлением в современной алгебре.Особый интерес вызывают такие вопросы, как силовские р -подгруппы, простые группы, представления группы и характеры группы.

Характеры группы играют важную роль в теории групп и её приложениях. Именно этим обуславливается актуальность и выбор темы исследования «Конечные группы с почти большим неприводимым характером».

Объект исследования: конечные группы.

Предмет исследования: характеры конечных групп.

Цель исследования: исследование конечных групп с почти большим неприводимым характером.

Цель исследования определила её задачи:

· провести анализ учебной и научной литературы по теме «Конечные группы» и «Характер конечной группы»;

· составить список конечных групп с почти большим неприводимым характером с помощью языка программирования GAP.

Курсовая работа состоит из введения, трех глав, заключения и списка использованной литературы.

В первой главе рассматриваются такие понятия каксиловские p -подгруппы, простые группы. Приведены доказательства трёх теоремСилова, теоремыБернсайда.

Во второй главе изучаются понятия представлений группы такие, как линейные представления и матричные представления, а также рассмотрены понятия характера группы.

В третьей главе рассмотрены краткая характеристика, история и возможности системы GAP, а также понятие конечной группы с почти большим неприводимым характером. С помощью GAPбыл составлен список конечных групп с почти большим неприводимым характером.

 

 

1 ТЕОРИЯ КОНЕЧНЫХ ГРУПП

 

1.1 Силовские p -подгруппы

 

Определения и утверждения, описанные в пункте 1.1, взяты из[6]. Рассмотрим ложность обращениятеоремы Лагранжа.

Согласно теореме Лагранжа, порядок подгруппы конечной группы является делителем порядка группы. Но, обратно, если мы имеем группу G порядка n и если n делится на m, то G может не иметь подгруппу порядка m. Например, можно проверить, что следующая группа подстановок порядка 12 не содержит подгрупп порядка 6:

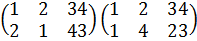
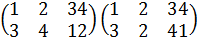
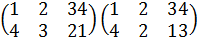
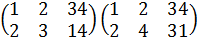
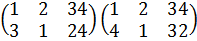
Однако эта группа имеет подгруппы порядков 2, 3 и 4.

Таким образом, если m делит n, мы, вообще говоря, не можем быть уверенными, что группа порядка n содержит подгруппу порядка m. Но если m – простое число или его степень, то всегда такая подгруппа существует. Вопрос о существовании и числе таких подгрупп выясняется в теоремах Силова. Мы начнем с теоремы, которая послужит отправной точкой для теорем Силова.

Теорема 1.1. Если порядок группы G делится на простое число p, то G содержит элемент порядка р.

Доказательство. Пусть n = mp порядок группы G. Если m =1, то G – циклическая группа порядка p, и теорема доказана. Будем проводить доказательство индукцией по m. Если G содержит истинную подгруппу Н, индекс которой [ G: H ] не делится на p, то порядок Н делится на р и, согласно предположению индукции, Н содержит элемент порядка p. Предположим теперь, что индекс любой истинной подгруппы группы G делится на р. Тогда ,где каждое 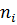обозначает число элементов в некотором классе сопряженных элементов группы G. При этом 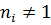есть индекс истинной подгруппы группы G, который, по предположению, делится на р. Можно считать, что 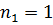, так как единица составляет класс. Поэтому количество 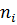, равных единице кратно р. Элемент 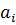составляет класс сопряженных элементов группы G тогда и только тогда, когда он принадлежит центру Z группы G. Таким образом, центр Z имеет порядок, кратный р. Но для любого z∊Z и любого g∊G имеем zg = gz. Следовательно, элементы центра Z перестановочны друг с другом, т.е. Z – абелева группа. Но теперь, согласно следствию из теоремы 3.3.1, Z содержит элемент порядка р.

Рассмотрим три теоремы Силова.

Если простое число р делит порядок группы G, то теорема 1.1 гарантирует существование по крайней мере одной подгруппы порядка р. Мы покажем теперь, что если G имеет порядок 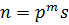, то она содержит также подгруппы порядков

Теорема 1.2 (Первая теорема Силова).Если G имеет порядок 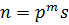, где р – простое число, которое не делит s, то G содержит подгруппы порядков 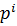(i= 1,…, m), причём каждая подгруппа порядка 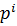(i= 1 ,…,m -1) инвариантна, по крайней мере, в одной подгруппе порядка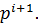

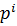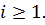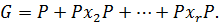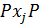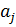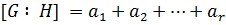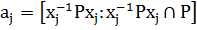Доказательство проведем индукцией по i. Как доказано выше, G содержит подгруппу порядка р. Пусть Р – подгруппа порядка , где Запишем G как сумму двойных смежных классов по Пусть состоит из правых смежных классов по Р. Тогда , где , и 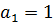для двойного класса Р ∙ 1 ∙ Р = Р. Поэтому или 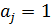, или есть степень числа р. Так как p делит [ G: Р ], число слагаемых 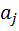, равных единице, должно быть кратным р. Если 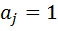, то 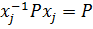,а потому и 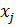и смежный класс 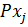= 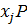принадлежит нормализатору К подгруппы Р. 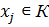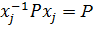Обратно, если , то и 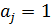. Таким образом, [ К: Р ]равно числу слагаемых 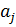, равных единице, а поэтому р делит [ К: Р ]. Следовательно, фактор-группа К/Р имеет порядок [ К: Р ], кратный р. Поэтому К/Р содержит подгруппу J* порядка р. По теореме 2.3.4, J*=J/P, где J 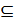K и [ J: P ] = [ J:1] =p, а поэтому J – подгруппа порядка 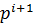, содержащая Р в качестве нормального делителя.

Определение 1.1. Группа Р называется р -группой, если все её элементы, отличные от единицы, имеют порядки, равные степеням простого числа р.

Определение 1.2. Подгруппа S группы G называется силовской р -подгруппой группы G, если S – p -подгруппа, не содержащаяся ни в какой другой р -подгруппе группы G.

Используя эти определения, мы можем сформулировать несколько следствий из первой теоремы Силова.

Следствие 1.1. Любая конечная группа G порядка 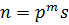, (p,s) = 1, p – простое, содержит силовскую р -подгруппу порядка 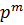, причем любая р -подгруппа содержится в некоторой силовской р -подгруппе группы G.

Любая группа порядка 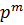является р-подгруппой. Согласно теореме 1.1, если порядок группы делится на два разных простых числа, то она не может быть р -группой. Следовательно, любая конечная р -группа имеет порядок, равный степени простого числа р, скажем,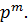

Следствие 1.2. Любая подгруппа р -группы Р порядка 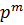содержится в некотрой максимальной подгруппе порядка 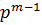, причем все максимальные подгруппы группы Р инвариантны в Р.

Теорема 1.3 (Вторая теорема Силова). В конечной группе G все силовские р -подгруппы сопряжены.

Доказательство. Пусть Р₁ и Р₂ – две силовские р -подгруппы. Тогда имеем разложение по двойному модулю: 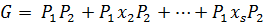. Пусть – число правых смежных классов по 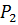в 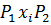. Иначе 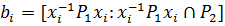, а поэтому либо равно единице, либо степени простого числа р. Но число 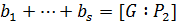не делится на р. Следовательно, 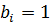для некоторого i и .

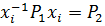Теорема 1.4 (Третья теорема Силова). Число силовских р -подгрупп конечной группы G равно и делит порядок группы G.

Доказательство. Это утверждение очевидно, если имеется только одна силовская р -подгруппа. В противном случае пусть 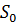– однаиз силовских р -подгрупп, а – все остальные. Если эти последние трансформировать элементами из 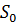, то они распадаются на некоторое число непересекающихся классов сопряженных (относительно 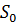) между собой подгрупп. Согласно второй теореме Силова, 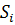– единственная силовская р -подгруппа в своем нормализаторе 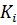. Следовательно, нормализатор подгруппы 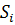в 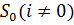является собственной подгруппой группы 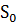, и тем самым число сопряженных с 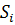относительно 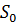подгрупп степени числа р, равно 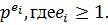Следовательно, 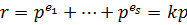, и число всех силовских р -подгрупп равно 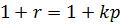. Число силовских р -подгрупп равно, согласно второй теореме Силова, индексу нормализатора группы 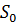, а потому делит порядок группы G.

Теорема 1.5. Пусть К –нормализаторсиловской р -подгруппы Р конечной группы G. Если Н –такая подгруппа, что 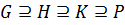, то H совпадает со своим нормализатором в G.

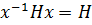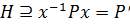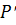Доказательство. Пусть . Тогда , где - силовская р-подгруппа в Н. Следовательно, существует такой элемент 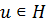, что 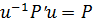, откуда 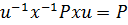, и тем самым 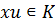, а отсюда 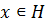, т.е. группа Н совпадает со своим нормализатором.

Следующая теорема, представляя самостоятельный интерес, допускает ряд важных применений, как это будет показано в последующих главах.

Теорема 1.6 (Бернсайда). Пусть G – конечная группа, h – её р-подгруппа, и пусть h содержится в двух различных силовских р -подгруппах, причем в одной из них является нормальным делителем, а в другой не является. Тогда h имеет , , 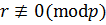сопряженных подгрупп 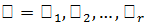, таких что

а) все 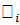инвариантны в группе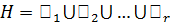

б) не существует такой силовской р -подгруппы, чтобы все группы 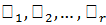были бы в ней нормальными делителями

в) подгруппы 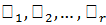составляют полный класс сопряженных подгрупп в группе 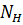– нормализаторе группы H.

Доказательство. Пусть 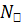–нормализатор подгруппы h. Пусть Q - силовская р -подгруппа группы G, в которой h не инвариантна, и такая, что группа 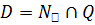максимальна. Пусть q – нормализатор D в Q, a 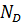– нормализатор D в G. Мы утверждаем, что . Действительно, h – инвариантная подгруппа индекса р в некоторой подгруппе группы Q, но h не является нормальным делителем в Q. Отсюда 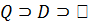. Кроме того, D как истинная подгруппа в Q строго содержится в своем нормализаторе q в Q. Итак, . Далее, так как 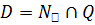, подгруппа h неинвариантна в q и тем более неинвариантна в 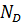. Пусть 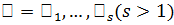– подгруппы, сопряженные с 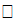в 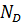. Так как 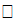– нормальный делитель в D и 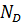индуцирует автоморфизмы в D, каждая подгруппа 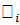также инвариантна в D и тем более в 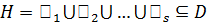.Нормализатор 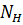подгруппы H содержит 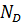, так как элементы из 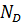трансформируют H в себя.

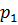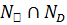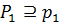Пусть –силовская подгруппа группы и –силовская подгруппа группы 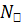. По условию 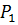–силовская подгруппа в G. Тогда 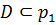, так как D не совпадает со своим нормализатором в 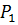. Теперь 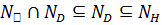. Пусть 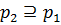–силовская подгруппа в 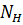и 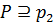– силовская подгруппа в G. Если 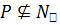, то 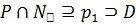, что противоречит свойству максимальности группы D. Следовательно, 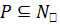, а поэтому 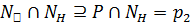, так как 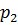–силовская подгруппа в .

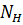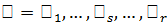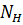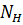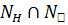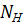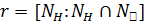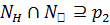Пусть – сопряженные с h относительно подгруппы (и, следовательно, все нормальные делители в H). Нормализатором подгруппы h в является , и поэтому число сопряженных с h в подгрупп равно . Но , где 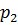–силовская подгруппа группы 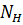. Следовательно, .

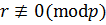Если бы все 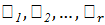были инвариантными подгруппами некоторой силовской подгруппы 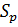, то 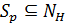и каждая силовская р -подгруппа группы 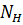содержала бы подгруппы 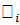в качестве нормальных делителей. Но 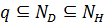– р -подгруппа в 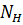, содержащая , но не в качестве нормального делителя.

Рассмотрим применение теоремы Силовак группам порядка pq. Теорема Силова часто дает весьма существенную информацию о данной конечной группе, а группы не очень большие – в том или ином смысле – позволяет описать полностью. В качестве иллюстрации дадим здесь описание групп порядка pq.

Пусть p, q – простые числа, р < q. Какой должна быть группа G порядка pq? Силовские р - и q -подгруппы из G, будучи подгруппами простого порядка, являются циклическими. Пусть (а), (b) – соответственно силовские р - и q -подгруппа. По теореме Силова число силовских q -подгрупп в G имеет вид 1 + kq и делит pq, поэтому силовская q -подгруппа (b) единственна. В частности, она нормальна в G. Число силовских р -подгрупп имеет вид 1 + kq и делит q, поэтому возможны два случая:

а)Силовская р -подгруппа (а) единственна. Тогда она нормальна и, значит,[ a,b ] ∊ (a) 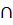(b) = 1. Так как 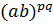= = 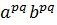1, то G = (ab). Таким образом, в этом случае G .

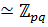б) Имеется q силовских р-подгрупп. Конечно, это возможно лишь при условии q 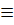1(mod p). Пусть 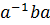= 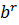. Если r =1, то снова G = (ab), т.е. G . Пусть r 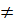1. Индукцией по х получаем 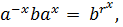откуда

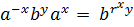
для всех целых х, у. При х = р, у = 1 это дает 1(mod q), кроме того, получаем формулу умножения

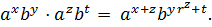(1.1)

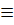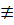Обратно, легко проверить, что если q 1(mod p), 1(mod q), r 1(mod q), то эта формула умножения определяет неабелеву группу порядка pq. Наконец, решения сравнения 1(mod q) составляют циклическую группу порядка р, поэтому те из них, которые 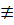1(mod q) имею вид , где r – одно из них. Все эти решения определяют одну и ту же группу,так как замена порождающегоa на 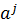приводит к замене r на .

Таким образом, с помощью теоремы Силовамы описали всевозможные типы групп порядка pq; их оказалось два – абелев и неабелев, причем второй существует только при условии q 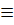1(mod p).

Примеры силовских подгрупп:

I.Аддитивная группа кольца вычетов 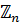разлагается в прямое произведение своих силовских р -подгрупп, которые являются циклическими подгруппами порядков 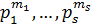, если n имеет каноническое разложение n = .

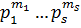II.Силовская р-подгруппа мультипликативной группы 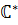– это квазициклическая группа .

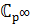III.Опишем силовские р -подгруппы симметрических групп. Как мы знаем, 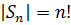Каков максимальный показатель е (n), при котором 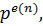при котором делит n!? В последовательности 1,2,…, n кратными р будут числа р,2р,…,кр, где к = 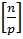, поэтому е (n) = 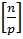+ е (к). так как 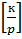= 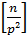, то e (n) = 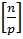+ +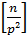… Удобно разложить n по основанию р:

n = 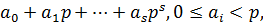(1.2)

тогда

e (n) = (1.3)

Рассмотрим сначала группы 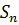, когда n – степень р. Пусть в 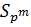уже найденасиловская р -подгруппа, т.е. подгруппа 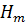порядка 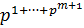; построим по ней в 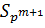подгруппу 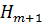порядка 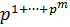. Для этого разобьем переставляемые символы 1,2,…, 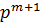на последовательные отрезки длины 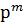. Если

с =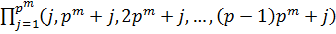

и x – подстановка на символах i -го отрезка, то легко сообразить, что – подстановка на символах (i + 1)-го отрезка (сложение по модулю р). Отсюда видно, что подгруппа, порожденная подгруппами 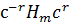, 0 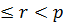, является их прямым произведением и, стало быть, подгруппа 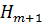, порожденная подгруппой 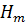и элементом с, изоморфна сплетению 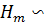(с). Подгруппа 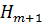– искомая, так как

.

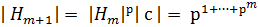Одновременно мы видим, что силовская р -подгруппа в 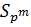изоморфна последовательному сплетению 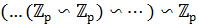циклической группы 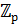с самой собою m раз.

Теперь пусть n произвольно. Разобьем символы 1,…,n на 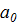одноэлементных, 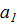р -элементных и т.д. отрезков (см. (1.2)). На каждом из этих отрезков рассмотрим симметрическую группу – она будет некоторой степени 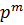, а в ней возьмем силовскую р-подгруппу, построенную как выше. Так как эти подгруппы действуют на непересекающихся множествах, то их порождение 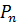является их прямым произведением, а потому имеет порядок:

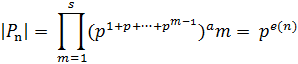
(см. (1.3)). Следовательно, 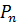- силовская р-подгруппа в 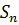. Из построения видно, что она изоморфна прямому произведению нескольких последовательных сплетений типа .

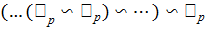IV. Рассмотрим, наконец, общие линейные группы над конечными полями. Пусть р – простое число, m, n – целые числа 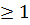и q = 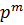. Покажем, что 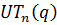– силовская р-подгруппа группы 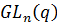. Подсчитаем порядки этих групп.

Какие n- ки над полем GF 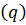могут быть первой строкой невырожденной матрицы? Очевидно, любые, кроме нулевой, т.е. 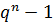штук. Если первая строка выбрана, то в качестве второй строки можно взять любую непропорциональную первой; таких строк 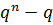. Если две первые строки уже выбраны, то в качестве третьей можно взять любую строку, не зависящую линейно от первых двух; это дает. 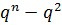возможностей. И так далее. Значит,

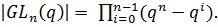(1.4)

Так как угловые элементы матриц из 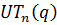пробегают независимо друг от друга всё поле, а всего угловых мест 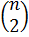, то 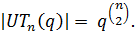Из сравнения порядков мы видим, что 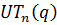- силовская р -подгруппа в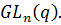

 

1.2 Простые группы

 

Определения и утверждения, описанные в пункте 1.2, взяты из [4].

Существуют группы 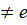, совпадающие со своим коммутантом и, стало быть, не являющиеся разрешимыми. Более того, мы сейчас установим существование неабелевых групп, в которых вообще нет нетривиальных (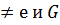) нормальных подгрупп. Такие группы принято называть простыми.

Лемма 2.3. Любая нормальная подгруппа К группы является объединением некоторого множества сопряженных классов группы .

Доказательство. Если 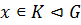, то и 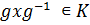для всех 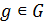. Следовательно, вместе с каждым элементом 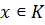в 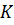содержится целиком класс сопряженных элементов 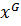и .

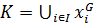Теорема 2.7. Знакопеременная группа 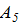простая.

Доказательство. Действительно, в группе 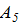, помимо единичной перестановки е, имеется 15 элементов (ij) (kl) порядка 2 (по три элемента этого вида в стационарной подгруппе каждой из точек 1, 2, 3, 4, 5), 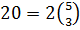элементов (ijk) порядка 3 и 24 = 4! Элемента (1 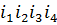) порядка 5. Элементы порядка 2 все сопряжены: они, очевидно, сопряжены в 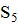, а так как стационарная подгруппа (относительно действия сопряжением) элемента (1 2)(3 4) содержит нечетную перестановку (1 2), то сопряжение может быть осуществлено четными перестановками. То же самое относится к элементам порядка 3. Но элементы порядка 5, сопряженные в 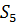, в группе 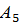распадаются на два класса с представителями (1 2 3 4 5) и (1 2 3 5 4). В самом деле, , а централизатором (стационарной подгруппой) элемента (1 2 3 4 5) в 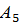служит циклическая группа порядка 5, порожденная этим элементом. Итак, мы имеем:

Таблица 1– Представители сопряженных классов

е	(1 2)(3 4)	(1 2 3)	(1 2 3 4 5)	(1 2 3 5 4)

В нижней строке указаны представители сопряженных классов, а в верхней – мощности этих классов. Пусть теперь К – нормальная подгруппа в 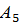. Согласно лемме 2.3

,

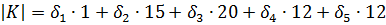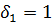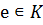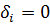где (так как ) и или 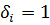при i = 2, 3, 4, 5. Нетрудно убедиться в том, что условие на 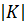быть делителем порядка 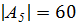(теорема Лагранжа) оставляет лишь две возможности:

а) 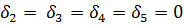; K – единичная подгруппа;

б) 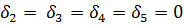; К = .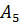

Это и доказывает, что 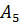– простая подгруппа.

Индукцией по n теперь можно установить, что простыми являются все группы 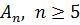(результат Э.Галуа). Так как подгруппы разрешимых групп разрешимы, то из теоремы 1во всяком случае следует, что симметрическая группа 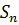неразрешима при .

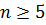Теорема 2.8. Группа вращений SO (3) является простой.

Доказательство. Согласно теореме 1 достаточно убедиться в том, что любая нормальная подгруппа К группы SU (2), содержащая ядро{ 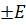} эпиморфизма Ф: 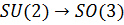и отличная от 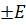, совпадает с SU (2). Соотношение 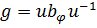можно интерпретировать по-новому, сказав, что в каждом сопряженном классе группы 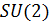содержится диагональная матрица 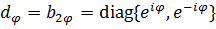. Так как по лемме К является объединением некоторого семейства сопряженных классов группы 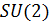, то без ограничения общности считаем 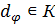для некоторого 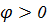такого, что .

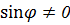В К должен содержаться также любой коммутатор

= ,

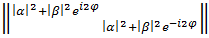где 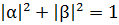. Для следа матрицы 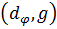получаем выражение

.

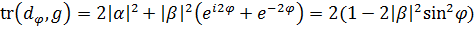Здесь 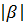принимает любое значение из отрезка [0, 1] и 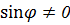. Снова в силу (5)найдется унитарная матрица h∊ 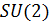такая,что 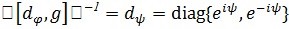, причем 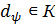. Так как 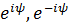− корни характеристического уравнения

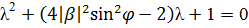
матрицы 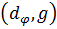, то, заставляя 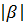пробегать значения от 0 до 1, мы получим для 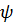любую точку на отрезке [0, 2 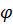]. Итак, в K содержится любой элемент 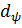и определенный параметром 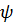сопряженный класс при 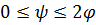. Поскольку для всякого 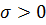найдется натуральное число n, удовлетворяющее условию 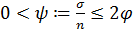, можно утверждать, что в K содержится наперёд заданный элемент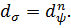

Теорема 2.9. Проективная специальная линейная группа PSL (2, F) над полем с числом элементов 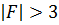простая.

Доказательство.

1) Выделим некоторые подгруппы и элементы:

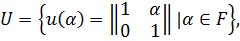
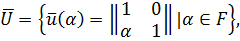
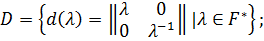
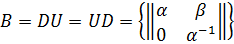
− стандартная борелевская подгруппа. Заметим, что

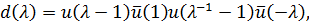
поэтому борелевская подгруппа B порождается унипотентными подгруппами Выделим ещё элемент

.

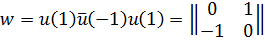2) Группа 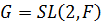обладает разложением

(1.5)

Чтобы в этом убедиться, рассмотрим естественное действие G слева на столбцы. Группа изотропии столбца 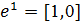совпадает, очевидно, с U. Орбита 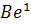состоит из всех столбцов [ 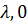], 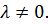С другой стороны, 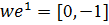, и поэтому орбита 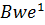состоит из всех столбцов 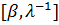со второй компонентой 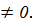Так как эти две орбиты покрывают орбиту 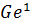, то отсюда следует, что 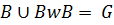, поскольку группа изотро