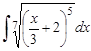ОГА ПОУ «Боровичский педагогический колледж»
Практические работы
По математическому анализу
Преподаватель: Н.П. Коваленко
Содержание
| 1. Тема – Предел функции | |
| 2. Тема – Производная функции | |
| 3. Тема – Исследование графика функции | |
| 4. Тема – Неопределенный интеграл | |
| 5. Тема – Определенный интеграл | |
| 8. Литература |
тема – ПРЕДЕЛ функции
Определение. Число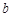 
называется пределом значений функции 
, 
, в точке 
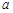, если для любой последовательности точек 
такой, что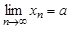 
последовательность 
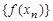значений функции 
в точках 
имеет своим пределом число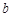
,
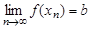в этом случае пишут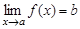 
.
Приведенное определение включает и особые случаи, когда числа 
и 
будут заменены символами 
и 
:
, 
, 
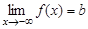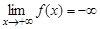и т.д.
Одним из важнейших результатов является равенство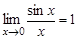 
, которое носит название первого замечательного предела.
А. Вычислить пределы:
1. 
2. 
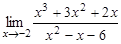
3. 
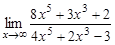
4. 
5. 
6. 
7. 
8. 
9. 
10. 
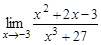
11. 
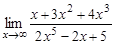
12. 
13. 
14. 
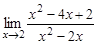
15. 
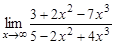
16. 
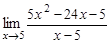
17. 
18. 
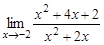
19. 
20. 
21. 
22. 
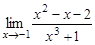
23. 
24. 
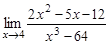
25. 
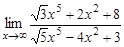
26. 
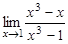
27. 
28. 
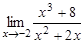
29. 
30. 
B. Вычислить пределы:
1. 
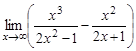
2. 
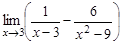
3. 
4. 
5. 
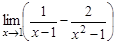
6. 
7. 
8. 
9. 
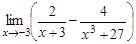
10. 
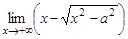
11. 
12. 
13. 
14. 
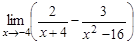
15. 
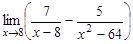
16. 
17. 
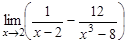
18. 
19. 
20. 
21. 
22. 
23. 
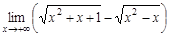
24.
25. 
26. 
27. 
28. 
29. 
30. 
тема – Производная функции
Определение. Производной функции 
в точке 
называется предел отношения приращения функции 
к вызвавшему его приращению аргумента 
, при стремлении приращения аргумента к нулю:
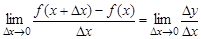
Если этот предел конечный, то функция 
называется дифференцируемой в точке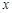 
; при этом она оказывается обязательно и непрерывной в этой точке. Если же предел равен 
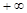или , то будем говорить, что функция 
имеет в точке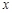 
бесконечную производную, однако при дополнительном условии, что функция в этой точке непрерывна.
A. Найти производные от функций:
1. 
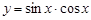
2. 
3. 
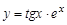
4. 
5. 
6. 
7. 
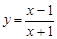
8. 
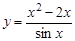
9. 
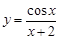
10. 
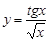
11. 
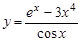
12. 
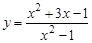
13. 
14. 
15. 
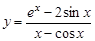
16. 
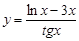
17. 
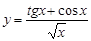
18. 
19. 
20. 
21. 
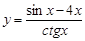
22. 
23. 
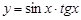
24. 
25. 
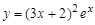
26. 
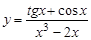
27. 
28. 
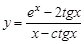
29. 
30. 
В. Найти производные от сложных функций:
1. 
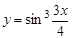
2. 
3. 
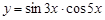
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
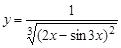
13. 
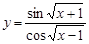
14. 
15. 
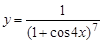
16. 
17. 
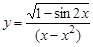
18. 
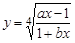
19. 
20. 
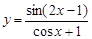
21. 
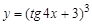
22. 
23. 
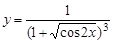
24. 
25. 
26. 
27. 
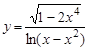
28. 
29. 
30. 
тема - исследование графика функции
Определение. Функция 
имеет экстремум (максимум или минимум) в точке 
, если 
является наибольшим или наименьшим значением функции в некоторой двусторонней окрестности этой точки.
Необходимое условие существования экстремума. Функция имеет экстремум в точке 
, если первая производная функции в этой точке равна нулю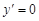 
или не существует.
Достаточные условия существования экстремума. Если функция непрерывна в точке и имеет в некоторой окрестности 
кроме, может быть, самой точки , конечную производную и если при переходе через :
· 
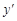меняет свой знак с + на -, то точка - точка максимума;
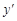· меняет свой знак с - на +, то точка - точка минимума;
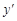· не меняет знака, то экстремума нет.
A. Исследовать функции и построить графики:
1. 
2. 
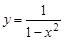
3. 
4. 
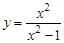
5. 
6. 
7. 
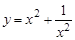
8. 
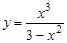
9. 
10. 
11. 
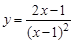
12. 
13. 
14. 
15. 
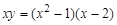
16. 
17. 
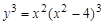
18. 
19. 
20. 
21. 
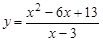
22. 
23. 
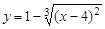
24. 
25. 
26. 
27. 
28. 
29. 
30. 
тема - неопределенный интеграл
Определение. Функция 
называется первообразной для функции 
на некотором промежутке, если для всех значений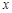 
из этого промежутка выполняется равенство 
.
Определение. Неопределенным интегралом 
называется множество всех первообразных функций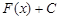 
для данной функции 
(где 
- произвольная постоянная):
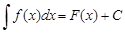
Отыскание неопределенного интеграла по данной подинтегральной функции или восстановление функции по ее производной называется интегрированием этой функции.
Одним из приемов для интегрирования функций является метод, основанный на следующей формуле:
,
где 
и 
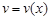- функции, имеющие непрерывные производные 
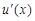и 
. Формула называется формулой интегрирования по частям неопределенного интеграла.
A. Вычислить интегралы:
1. 
2. 
3. 
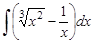
4. 
5. 
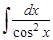
6. 
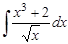
7. 
8. 
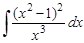
9. 
10. 
11. 
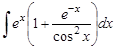
12. 
13. 
14. 
15. 
16. 
17. 
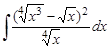
18. 
19. 
20. 
21. 
22. 
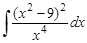
23. 
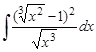
24. 
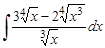
25. 
26. 
27. 
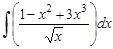
28. 
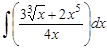
29. 
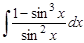
30. 
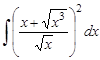
B. Вычислить интегралы, используя замену переменной:
1. 
2. 
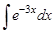
3. 
4. 
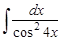
5. 
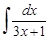
6. 
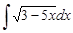
7. 
8. 
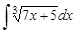
9. 
10. 
11. 
12. 
13. 
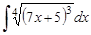
14. 
15. 
16. 
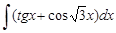
17. 
18. 
19. 
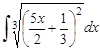
20. 
21. 
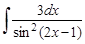
22. 
23. 
24. 
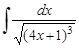
25. 
26. 
27. 
28. 
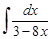
29. 
30. 