Тема. Определенный интеграл
В общем виде определенный интеграл записывается так:
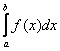
По сравнению с неопределенным интегралом прибавились пределы интегрирования.
Нижний предел интегрирования стандартно обозначается буквой 
.
Верхний предел интегрирования стандартно обозначается буквой 
.
Отрезок 
называется отрезком интегрирования.
Что такое определенный интеграл? Это ЧИСЛО.
Есть ли у определенного интеграла геометрический смысл? Есть.
Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.
Как решить определенный интеграл? С помощью формулы Ньютона-Лейбница:
Этапы решения определенного интеграла:
1) Сначала найти первообразную функцию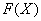 
(неопределенный интеграл). Константа 
в определенном интеграле никогда не добавляется. Запись 
является подготовкой для применения формулы Ньютона-Лейбница.
2) Подставить значение верхнего предела в первообразную функцию: 
.
3) Подставить значение нижнего предела в первообразную функцию: 
.
4) Рассчитать разность 
, то есть, найти число.
Всегда ли существует определенный интеграл? Нет, не всегда.
Например, интеграла 
не существует, поскольку отрезок интегрирования 
не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными).
Что нужно, чтобы определенный интеграл существовал? Для того чтобы определенный интеграл существовал, необходимо чтобы подынтегральная функция была непрерывной на отрезке интегрирования.
Прежде чем приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования.
Может ли определенный интеграл быть равен отрицательному числу? Может.
|
|
Может ли нижний предел интегрирования быть больше верхнего предела интегрирования? Может.
– интеграл вычисляется по формуле Ньютона-Лейбница.
Некоторые свойства определенного интеграла.
1. В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:
Например, в определенном интеграле перед интегрированием целесообразно поменять пределы интегрирования на «привычный» порядок:
– в таком виде интегрировать значительно удобнее.
2. Как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:
– это справедливо не только для двух, но и для любого количества функций.
3. Для определенного интеграла справедлива формула интегрирования по частям:
Пример 1
Вычислить определенный интеграл
Решение:
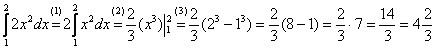
(1) Выносим константу за знак интеграла.
(2) Интегрируем по таблице с помощью формулы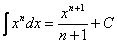 
. Появившуюся константу 
желательно отделить от 
и вынести за скобку.
(3) Используем формулу Ньютона-Лейбница 
. Сначала подставляем в верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.
Пример 2
Вычислить определенный интеграл
Решение:
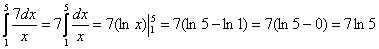
Пример 3
Вычислить определенный интеграл
Решение:
(1) Используем свойства линейности определенного интеграла.
(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.
(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница:
Особое внимание обратите на третье слагаемое: 
–очень часто машинально пишут 
(особенно, когда подстановка верхнего и нижнего предела проводится устно и не расписывается так подробно). Еще раз внимательно изучите вышерассмотренный пример.
|
|
Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. Решение можно сократить:
Пример 4
Вычислить определенный интеграл
Решение:
