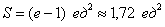Пример 5
Вычислить определенный интеграл
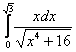
Главный вопрос здесь вовсе не в определенном интеграле, а в том, как правильно провести замену.
Смотрим по таблице интегралов на что больше всего похожа подынтегральная функция?
 .
.
Но в табличном интеграле под корнем 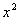 , а в нашем – «икс» в четвёртой степени.
, а в нашем – «икс» в четвёртой степени.
Сначала готовим наш интеграл к замене:

Из вышеуказанных соображений замена: 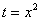
Таким образом, в знаменателе будет всё хорошо: 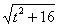 .
.
Выясняем, во что превратится оставшаяся часть  подынтегрального выражения, для этого находим дифференциал
подынтегрального выражения, для этого находим дифференциал 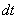 :
:
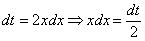
Дополнительный этап. Находим новые переделы интегрирования.
Смотрим на нашу замену 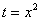 и старые пределы интегрирования
и старые пределы интегрирования  ,
, 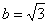 .
.
Сначала подставляем в выражение замены 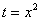 нижний предел интегрирования, то есть, ноль:
нижний предел интегрирования, то есть, ноль:
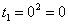
Потом подставляем в выражение замены 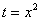 верхний предел интегрирования, то есть, корень из трёх:
верхний предел интегрирования, то есть, корень из трёх:
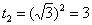
Готово. Продолжаем решение.

(1) В соответствии с заменой записываем новый интеграл с новыми пределами интегрирования.
(2) Это простейший табличный интеграл, интегрируем по таблице. Константу 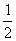 лучше оставить за скобками (можно этого и не делать), чтобы она не мешалась в дальнейших вычислениях. Справа отчеркиваем линию с указанием новых пределов интегрирования
лучше оставить за скобками (можно этого и не делать), чтобы она не мешалась в дальнейших вычислениях. Справа отчеркиваем линию с указанием новых пределов интегрирования 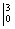 – это подготовка для применения формулы Ньютона-Лейбница.
– это подготовка для применения формулы Ньютона-Лейбница.
(3) Используем формулу Ньютона-Лейбница  .
.
Ответ стремимся записать в максимально компактном виде.
Ещё одно отличие от неопределенного интеграла состоит в том, что, после того, как мы провели замену, никаких обратных замен проводить не надо.
Пример 6
Вычислить определенный интеграл
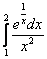
Решение:
Замена: 
Новые пределы интегрирования:
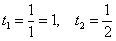
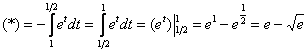
Метод интегрирования по частям в определенном интеграле

Формулу Ньютона-Лейбница здесь необходимо применить дважды: для произведения 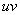 и, после того, как мы возьмем интеграл
и, после того, как мы возьмем интеграл 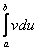 .
.
Пример 7
Вычислить определенный интеграл

Решение:
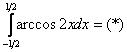
Интегрируем по частям:
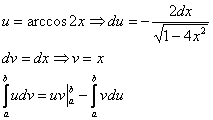
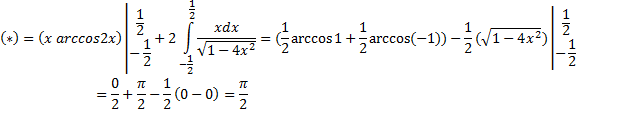
Вычисление площадей плоских фигур
Задание «вычислить площадь с помощью определенного интеграла» всегда предполагает построение чертежа.
Криволинейной трапецией называется плоская фигура, ограниченная графиком некоторой функции  , осью
, осью  и прямыми
и прямыми 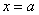 ,
, 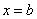 :
:
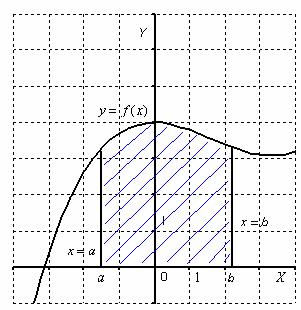
Площадь криволинейной трапеции численно равна определенному интегралу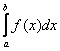 .
.
С точки зрения геометрии определенный интеграл – это ПЛОЩАДЬ. То есть, определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры.
Пример 8
Вычислить площадь фигуры, ограниченной линиями 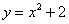 ,
, 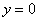 ,
, 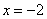 ,
, 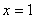 .
.
Первый и важнейший момент решения – построение чертежа.
Выполним чертеж (обратите внимание, что уравнение 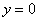 задает ось
задает ось  ):
):
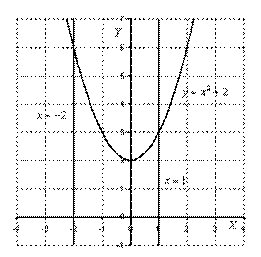
На отрезке 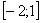 график функции
график функции 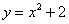 расположен над осью
расположен над осью , поэтому:
, поэтому:
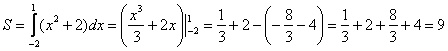
Ответ: 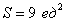
Пример 9
Вычислить площадь фигуры, ограниченной линиями  ,
, 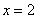 ,
, 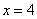 и осью
и осью 
Решение:
Выполним чертеж:
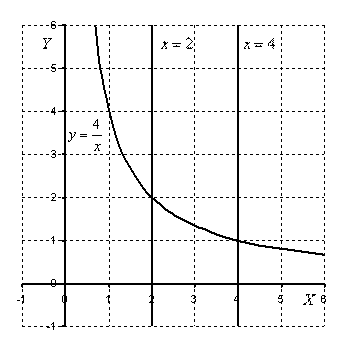
На отрезке  график функции
график функции 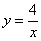 расположен над осью
расположен над осью  , поэтому:
, поэтому:
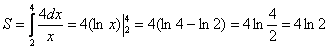
Ответ: 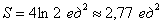
Пример 10
Вычислить площадь фигуры, ограниченной линиями  ,
, 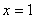 и координатными осями.
и координатными осями.
Решение: Выполним чертеж:
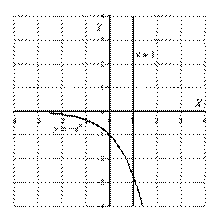
Если криволинейная трапеция полностью расположена под осью , то её площадь можно найти по формуле:
, то её площадь можно найти по формуле: 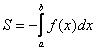
В данном случае:
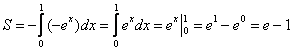
Ответ: