План
- Векторное пространство
. Понятие метрики. Свойства метрики - Внутренняя точка множества.Открытое множество в пространстве
- Свойства открытых множеств
- Предельная точка множества. Замкнутые множества в пространстве
- Свойства замкнутых множеств в пространстве
1. Векторное пространство . Понятие метрики. Свойства метрики
Пусть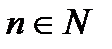 
. Элементы пространства - это вектора 
, где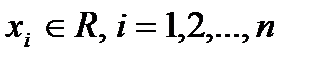 
. В пространстве введены две операции: сложение векторов и умножение вектора на скаляр, свойства которых рассматриваются в курсе алгебры и геометрии.
Определим норму вектора как функцию:
.
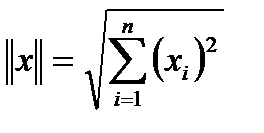Функция нормы вектора удовлетворяет свойствам:
1. 
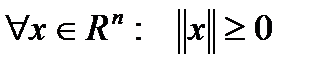і 
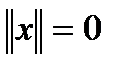тогда и только тогда, когда 
;
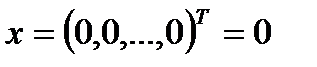2. 
;
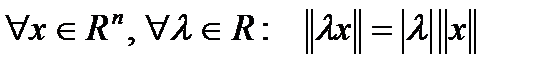3. 
.
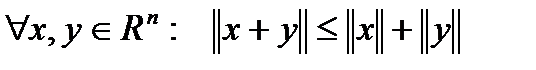Определение 1. Расстоянием в пространстве между векторами 
называется
.
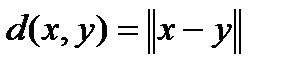Свойства расстояния:
1. 
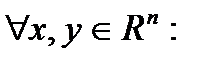
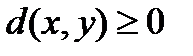і 
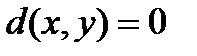тогда и только тогда, когда 
;
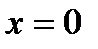2. 
.
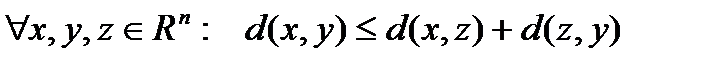2. Внутренняя точка множества.Открытое множество в пространстве
Определение 2. Пусть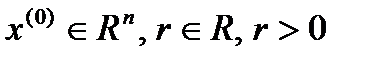 
. Открытым шаром радиуса 
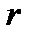с центром в точке 
(обозначается 
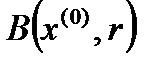) называется множество точек 
таких, что
.
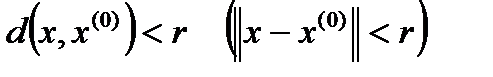Пример. 
- это интервал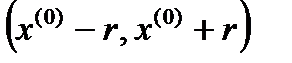 
(рис.1).
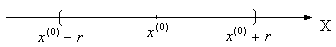
Рис.1.
Пример. 
(рис.2).
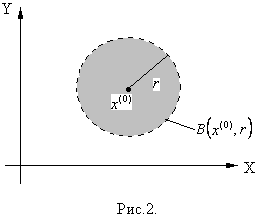
Определение 3. Пусть 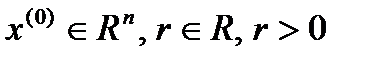. Замкнутым шаром радиуса 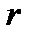с центром в точке (обозначается 
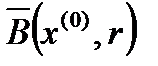) называется множество точек таких, что
.
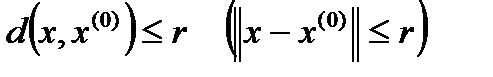Определение 4. Точка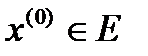 
называется внутренней точкой этого множества, если существует такой открытый шар 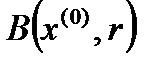, который полностью находится во множестве 
.
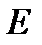Определение 5. Множество 
называется открытым множеством, если каждая его точка является внутренней точкой.
Пример. Пустое множество и множество 
- открытые множества.
Пример. Доказать, что 
- открытое множество (рис.3).
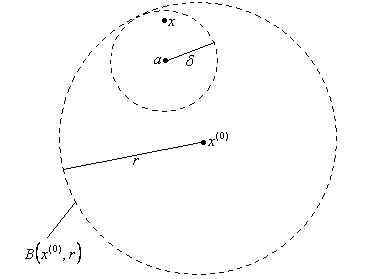
Рис.3.
Возьмем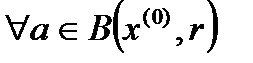 
. Это означает, что 
. Обозначим 
. Рассмотрим открытый шар 
. Докажем, что 
. Для этого покажем, что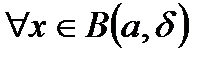 
одновременно принадлежит 
:
.
Таким образом, 
, а это означает, что 
.
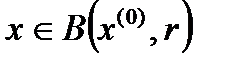Определение 6. Открытым параллелепипедом в 
называется множество точек 
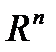, для которых выполняются неравенства:
,
,
...
,
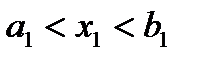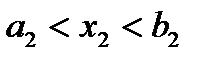где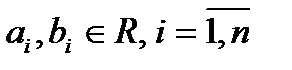 
.
Задание. Показать, что открытый параллелепипед является открытым множеством.
Свойства открытых множеств
Теорема 1. Пересечение любого конечного числа открытых множеств является открытым множеством.
Доказательство. Пусть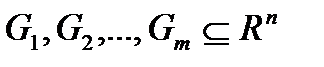 
- открытые множества, 
. Покажем, что 
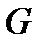- открытое множество. Для этого возьмем 
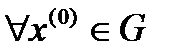и покажем, что эта точка является внутренней для :
.
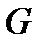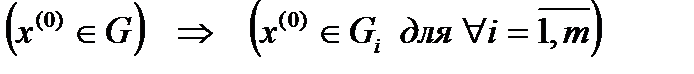Поскольку каждое множество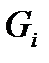 
открыто, то для 
найдется открытый шар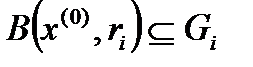 
. Обозначим 
. Тогда
Таким образом, 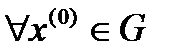является для этого множества внутренней, а само множество 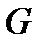- открытым.
Замечание. Пересечение бесконечного числа открытых множеств может и не быть открытым множеством.
Пример. Рассмотрим бесконечную совокупность открытых множеств 
Для них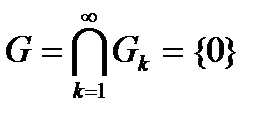 
. Множество 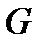, которое содержит одну точку, не является открытым.
Теорема 2. Объединение любого числа открытых множеств является открытым множеством.
Доказательство. Пусть 
- некоторое множество индексов 
. Пусть для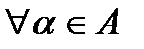 
множество 
является открытым. Рассмотрим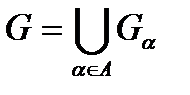 
. Покажем, что 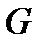- открытое. Для этого возьмем 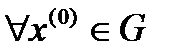и покажем, что эта точка является внутренней для :
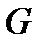, что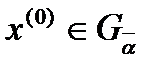 
.
Поскольку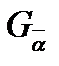 
- открытое множество, то 
, тогда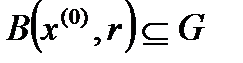 
, а это означает, что 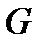- открытое множество.
4. Предельная точка множества. Замкнутые множества в пространстве
Определение 7. Пусть множество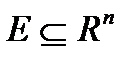 
. Точка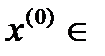 
называется предельной для множества 
, если любой открытый шар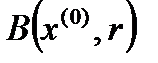 
с центром в этой точке содержит точки множества , которые отличаются от точки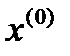 
.
Определение8. Открытый шар с центром в точке 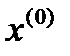называется окрестностью точки .
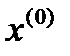Замечание. Если точка 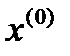является предельной для множества , то любая окрестность этой точки содержит бесконечно много точек из множества .
Замечание. Если точка 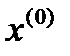является внутренней для множества , то она будет и предельной точкой этого множества.
Определение9. Множество 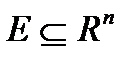называется замкнутым, если оно включает в себя все свои предельные точки.
Пример. Множество 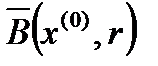является замкнутым.
Пример. Пустое множество и - замкнутые множества.
Определение10. Пусть множество 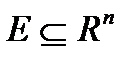. Дополнение к множеству называется совокупность точек 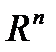и одновременно не принадлежат множеству .
Теорема 3. Множество открыто тогда и только тогда, когда его дополнение будет замкнутым.
5. Свойства замкнутых множеств в пространстве
Теорема 4. Пересечение любого числа замкнутых множеств является замкнутым множеством.
Доказательство. Самостоятельно.
Теорема 5. Объединение любого конечного числа замкнутых множеств является замкнутым множеством.
Доказательство. Самостоятельно.
Замечание. Объединение бесконечного числа замкнутых множеств может и не быть замкнутым множеством.
Пример. Рассмотрим бесконечную совокупность замкнутых множеств 
Для них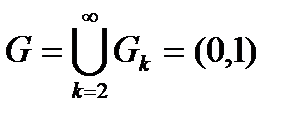 
- открытое множество.