Лекция 22. Непрерывность функции многих переменных
План
- Определение непрерывной функции многих переменных. Понятие изолированной точки
- Непрерывность суммы, произведения, частного непрерывных функций многих переменных
- Сложная функция и ее непрерывность
- Непрерывные функции на компактах
- Равномерная непрерывность функции многих переменных
Определение непрерывной функции многих переменных. Понятие изолированной точки
Определение 1. Пусть
,
а точка 
. Говорят, что функция 
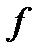непрерывна в точке 
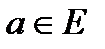, если
для 
, что для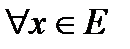 
такого, что 
выполняется
.
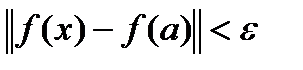Из определения 1 вытекает, что для точки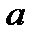 
, в которой функция 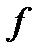является непрерывной, возможны два варианта:
1. Пусть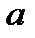 
- предельная точка множества 
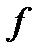. Тогда функция будет непрерывной в точке 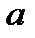, если 
.
2. Пусть не является предельной точкой множества . Такая точка множества называется его изолированной точкой. Поскольку 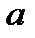не является предельной, то 
, который не содержит других точек множества , кроме :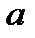 
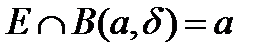. Тогда для 
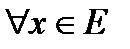, который удовлетворяет условию: 
, будет выполняться неравенство: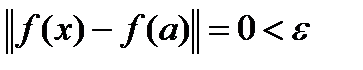 
для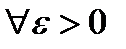 
, поскольку 
, который удовлетворяет условию: , только один - 
. Таким образом, если множество имеет изолированные точки, то 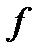непрерывна в каждой из них.
Пусть . Такая функция определяет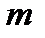 
действительных функций: 
.
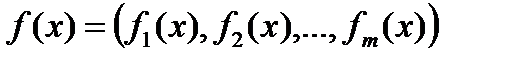Теорема 1. Для того, чтобы функция , , 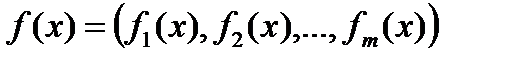была непрерывна в точке необходимо и достаточно, чтобы каждая из действительных функций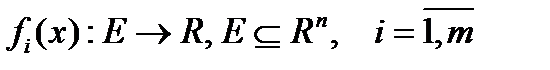 
, была непрерывна в точке 
.
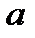Непрерывность суммы, произведения, частного непрерывных функций многих переменных
Теорема 2. Пусть определены функции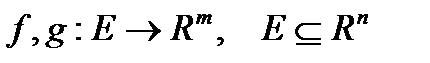 
. Если 
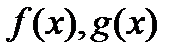непрерывны в точке , то
· 
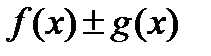- непрерывны в точке ;
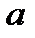· Если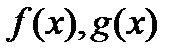 
- действительные функции, то 
непрерывна в точке ;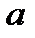
· Если 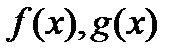- действительные функции и 
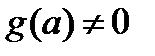то 
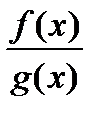непрерывна в точке .
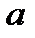Сложная функция и ее непрерывность
Пусть
,
и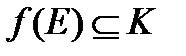 
. Тогда на множестве 
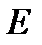определена функция 
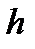, которая называется сложной функцией:
. (10)
Теорема 3 (о непрерывности сложной функции). Пусть на множестве 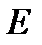определена сложная функция (10). Если функция 
непрерывна в точке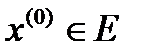 
, а функция 
непрерывна в соответствующей точке 
, то сложная функция 
непрерывна в точке .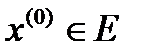
Определение 2. Пусть . Говорят, что функция 
непрерывна на множестве 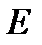, если она непрерывна в каждой точке этого множества.
Пример. Рассмотрим совокупность функций:
.
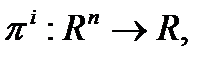
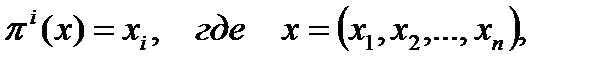
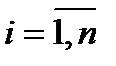Эти функции непрерывны в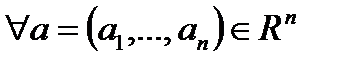 
. Действительно, рассмотрим
.
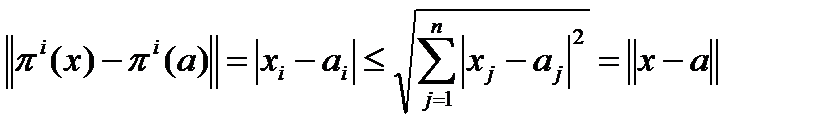Зададим произвольно 
, пусть 
. Тогда для 
такого, что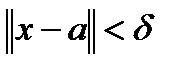 
, будет выполняться: 
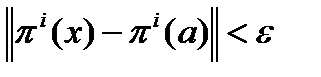, т.е. функции 
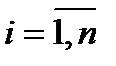, , непрерывны в 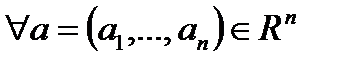, т.е. непрерывны в пространстве 
.
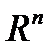Пример. Рассмотрим совокупность функций:
,
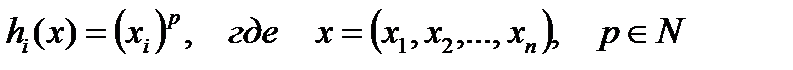Т.е. 
.
Докажем, что функции 
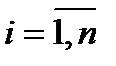, , непрерывны в любой точке пространства 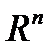. Функции являются сложными функциями: 
. Внешняя функция одной переменной 
непрерывна в 
, функции 
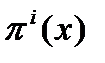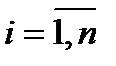, , непрерывны на 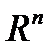, тогда по предыдущей теореме сложные функции , , 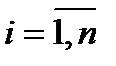непрерывны в пространстве .
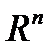Непрерывные функции на компактах
Определение 3. Функция называется ограниченной на множестве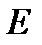 
, если 
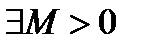, что 
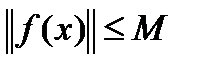для 
.
Теорема 4 (Вейерштрасса). Пусть , 
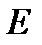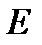непрерывна на , - компакт, тогда 
ограничена на множестве .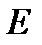
Доказательство. Допустим, что 
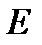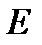непрерывна на , - компакт, но неограничена на множестве 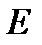. Тогда для 
такой, что
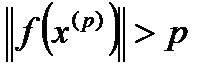. (20)
Таким образом можно построить векторную последовательность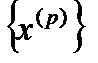 
, 
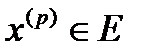для .
Множество 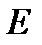- компакт, поэтому 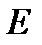- ограниченное множество, а потому построенная последовательность 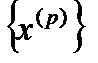тоже ограничена. По лемме Больцано-Вейерштрасса из каждой ограниченной последовательности можно выделить сходящуюся подпоследовательность 
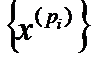. Для элементов этой подпоследовательности выполняется условие (20), т.е.
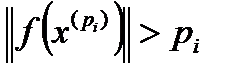. (30)
Обозначим: 
.
Поскольку 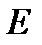- компакт, то 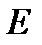- замкнутое множество, т.е. содержит все свои предельные точки, поэтому 
. Функция непрерывна на 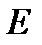, потому непрерывна в точке 
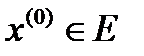, а это означает, что
.
Но из (30) вытекает, что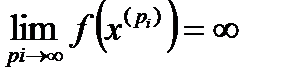 
.
Получили противоречие, поэтому наше предположение о неограниченности функции является ложным.