3.2.1. Даны две точки 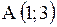 и
и  . Найти: 1) уравнение прямой
. Найти: 1) уравнение прямой  ; 2) угловой коэффициент к этой прямой; 3) угол наклона прямой к оси
; 2) угловой коэффициент к этой прямой; 3) угол наклона прямой к оси  .
.
3.2.2. Даны три точки 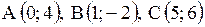 . Найти: 1) уравнение прямой
. Найти: 1) уравнение прямой 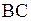 ; 2) уравнение прямой проходящей через точку
; 2) уравнение прямой проходящей через точку  параллельно прямой
параллельно прямой 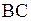 ; 3) уравнение прямой проходящей через точку
; 3) уравнение прямой проходящей через точку  перпендикулярно прямой
перпендикулярно прямой 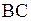 .
.
3.2.3. Найти проекцию точки 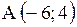 на прямую
на прямую  .
.
3.2.4. Найти точку  симметричную точке
симметричную точке  относительно прямой
относительно прямой  .
.
3.2.5. Через точку пересечения прямых  и
и  провести прямую: 1) перпендикулярно прямой
провести прямую: 1) перпендикулярно прямой  ; 2) параллельно этой прямой.
; 2) параллельно этой прямой.
3.2.6. Под каким углом прямая  пересекает ось
пересекает ось  ?
?
3.2.7. Найти угол между прямыми: 1)  и
и  ; 2)
; 2)  и
и  .
.
3.2.8. Найти расстояние между двумя параллельными прямыми  и
и  .
.
3.2.9. Найти уравнение прямой, проходящей через точку  и удаленной от начала координат на расстояние 5 ед. масштаба.
и удаленной от начала координат на расстояние 5 ед. масштаба.
3.2.10. Даны две противоположные вершины квадрата  ,
,  . Составить уравнения его сторон.
. Составить уравнения его сторон.
3.2.11. Даны две вершины треугольника  и
и  и точка пересечения его высот
и точка пересечения его высот  . Найти уравнение сторон треугольника.
. Найти уравнение сторон треугольника.
3.2.12. Треугольник  задан координатами своих вершин
задан координатами своих вершин  ,
,  ,
,  . Требуется: 1) написать уравнение стороны
. Требуется: 1) написать уравнение стороны  ; 2) написать уравнение высоты
; 2) написать уравнение высоты  и вычислить ее длину
и вычислить ее длину  ; 3) найти угол
; 3) найти угол  между высотой
между высотой  и медианой
и медианой  ; 4) написать уравнение биссектрис
; 4) написать уравнение биссектрис  ,
,  внутреннего и внешнего углов при вершине
внутреннего и внешнего углов при вершине  .
.
3.2.13. Составить уравнения сторон треугольника, зная его вершину  , а также уравнения биссектрисы
, а также уравнения биссектрисы  и медианы
и медианы  , проведенных из одной вершины.
, проведенных из одной вершины.
3.2.14. На прямой  найти такую точку
найти такую точку  , сумма расстояний которой до точек
, сумма расстояний которой до точек  и
и  была бы наименьшей.
была бы наименьшей.
3.2.15. На прямой  найти такую точку
найти такую точку  , разность расстояний которой до точек
, разность расстояний которой до точек  и
и  была бы наибольшей.
была бы наибольшей.
3.2.16. Составить уравнения сторон треугольника, если даны одна из его вершин  и уравнения двух высот
и уравнения двух высот  и
и  .
.
3.2.17. Найти уравнения сторон треугольника, зная одну его вершину  , а также уравнения высоты
, а также уравнения высоты  и медианы
и медианы  , проведенных из одной вершины.
, проведенных из одной вершины.
3.2.18. Среди прямых, проходящих через точку 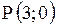 , найти такую, отрезок которой, заключенный между прямыми
, найти такую, отрезок которой, заключенный между прямыми  , делится в точке
, делится в точке  пополам.
пополам.
3.2.19. Точка  является вершиной квадрата, одна из сторон которого лежит на прямой
является вершиной квадрата, одна из сторон которого лежит на прямой 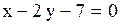 . Вычислить площадь этого квадрата.
. Вычислить площадь этого квадрата.
3.2.20. Две стороны квадрата лежит на прямых 
 . Вычислить его площадь.
. Вычислить его площадь.
3.2.21. Даны две смежные вершины квадрата  и
и  . Составить уравнения его сторон.
. Составить уравнения его сторон.
3.2.22. Луч света направлен по прямой  . Дойдя до прямой
. Дойдя до прямой  луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.
луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.
3.2.23. Составить уравнение прямой, проходящей через точку пересечения прямых  и отстоящей от точки
и отстоящей от точки  на расстоянии
на расстоянии 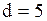 .
.
3.2.24. Написать уравнение окружности, проходящей через три точки:  ,
,  ,
,  .
.
3.2.25. Составить уравнение окружности, проходящей через точки  ,
,  , если ее центр лежит на прямой
, если ее центр лежит на прямой  .
.
3.2.26. Вычислить расстояние от центра окружности  до прямой, проходящей через точки пересечения окружностей
до прямой, проходящей через точки пересечения окружностей  ,
,  .
.
3.2.27. Составить уравнение касательной к окружности  в точке
в точке 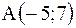 .
.
3.2.28. Дан эллипс  . Найти: 1) его полуоси; 2) координаты фокусов; 3) эксцентриситет; 4) уравнения директрис.
. Найти: 1) его полуоси; 2) координаты фокусов; 3) эксцентриситет; 4) уравнения директрис.
3.2.29. Вычислить площадь четырехугольника, две вершины которого лежат в фокусах эллипса  , две другие совпадают с концами его малой оси.
, две другие совпадают с концами его малой оси.
3.2.30. Прямая  касается эллипса, фокусы которого находятся в точках
касается эллипса, фокусы которого находятся в точках 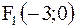 и
и  . Составить уравнение этого эллипса.
. Составить уравнение этого эллипса.
3.2.31. Точка  является концом малой оси эллипса, фокусы которого лежат на прямой
является концом малой оси эллипса, фокусы которого лежат на прямой  . Составить уравнение этого эллипса, зная его эксцентриситет
. Составить уравнение этого эллипса, зная его эксцентриситет  .
.
3.2.32. Дана гипербола  . Найти: 1) координаты ее центра
. Найти: 1) координаты ее центра  ; 2) полуоси; 3) эксцентриситет; 4) уравнения асимптот; 5) уравнения директрис.
; 2) полуоси; 3) эксцентриситет; 4) уравнения асимптот; 5) уравнения директрис.
3.2.33. Составить уравнение гиперболы, фокусы которой лежат в вершинах эллипса  , а директрисы проходят через фокусы этого эллипса.
, а директрисы проходят через фокусы этого эллипса.
3.2.34. Найти острый угол между асимптотами гиперболы, если ее эксцентриситет равен 2.
3.2.35. Составить уравнение гиперболы, если известны ее эксцентриситет  , фокус
, фокус 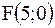 и уравнение соответствующей директрисы
и уравнение соответствующей директрисы  .
.
3.2.36. Парабола симметрична относительно оси  , проходит через точку
, проходит через точку  , а вершина ее лежит в начале координат. Составить ее уравнение.
, а вершина ее лежит в начале координат. Составить ее уравнение.
3.2.37. Установить, какие линии определяются следующими уравнениями:
1)  ; 2)
; 2)  ;
;
3)  ;
;
4) 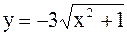 ; 5)
; 5) 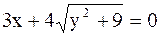 ;
;
6) 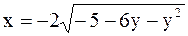 ;
;
7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10)  ; 11)
; 11)  .
.
3.2.38. Найти канонические уравнения прямой, проходящей через точки  и
и  , если: 1)
, если: 1)  ; 2)
; 2)  .
.
3.2.39. Найти параметрические уравнения прямой, проходящей через точки  и
и  , если: 1)
, если: 1)  ; 2)
; 2)  .
.
3.2.40. Найти общие уравнения прямой заданной в канонической форме:
1) 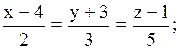 2)
2) 
3.2.41. Найти общие уравнения прямой, заданной в параметрической форме:
1) 
| 2) 
| 3) 
|
3.2.42. Найти канонические уравнения прямой заданной общими уравнениями: 1)  2)
2) 
3.2.43. Найти параметрические уравнения прямой заданной общими уравнениями: 1)  2)
2) 
3.2.44. Доказать параллельность прямых:
1) 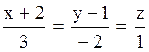 и
и 
2) 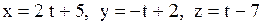 и
и 
3)  и
и 
3.2.45. Доказать перпендикулярность прямых:
1)  и
и 
2)  и
и 
3)  и
и 
3.2.46. Найти острый угол между прямыми:

3.2.47. Определить косинус угла между прямыми


3.2.48. Доказать, что прямые заданные параметрическими уравнениями  и
и  пересекаются.
пересекаются.
3.2.49. При каком значении  прямые
прямые 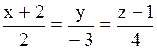 ,
,  пересекаются?
пересекаются?
3.2.50. Составить уравнение плоскости:
1) параллельной оси  и проходящей через точки
и проходящей через точки  и
и  ;
;
2) параллельной плоскости  и проходящей через точку
и проходящей через точку  ;
;
3) проходящей через ось  и через точку
и через точку  .
.
3.2.51. Найти расстояние между параллельными плоскостями 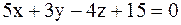 ,
,  .
.
3.2.52. Найти уравнение плоскости, проходящей через точку  параллельно плоскости
параллельно плоскости  .
.
3.2.53. Через точки  и
и  провести плоскость перпендикулярно плоскости
провести плоскость перпендикулярно плоскости  .
.
3.2.54. Составить уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям  ,
, 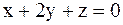 .
.
3.2.55. Написать уравнение плоскости, проходящей через три заданные точки: 1) 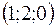 ,
,  ,
,  ; 2)
; 2)  ,
,  ,
,  .
.
3.2.56. Найти острый угол между прямыми
 и
и 
3.2.57. Через точку  провести прямую, параллельную оси
провести прямую, параллельную оси  .
.
3.2.58. Написать каноническое уравнение прямой, проходящей через точку  параллельно: 1) вектору
параллельно: 1) вектору  ;
;
2) прямой  ;
;
3) оси  ; 4) оси
; 4) оси  ; 5) прямой
; 5) прямой 
6) прямой  ,
,  ,
,  .
.
3.2.59. Найти уравнение плоскости, проходящей через точку  перпендикулярно прямой
перпендикулярно прямой  .
.
3.2.60. Найти точку пересечения прямой  с плоскостью
с плоскостью  .
.
3.2.61. Составить уравнение плоскости, проходящей через точку  и прямую
и прямую  .
.
3.2.62. Найти уравнение плоскости, проходящей через прямую  перпендикулярно плоскости
перпендикулярно плоскости  .
.
3.2.63. Найти уравнение плоскости, проходящей через две параллельные прямые:  и
и 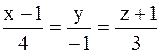 .
.
3.2.64. Установить тип заданных поверхностей и построить их:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ;
;
8) 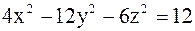 .
.
3.2.65. Составить уравнение плоскостей, касательных к сфере  и параллельных плоскости
и параллельных плоскости  .
.
3.2.66. Установить, при каких значениях  плоскость
плоскость  пересекает двуполостный гиперболоид
пересекает двуполостный гиперболоид  : 1) по эллипсу; 2) по гиперболе.
: 1) по эллипсу; 2) по гиперболе.
ОТВЕТЫ
3.2.1. 1)  2)
2)  3)
3)  .
.
3.2.2. 1)  2)
2) 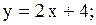 3)
3) 
3.2.3.  .
.
3.2.4. 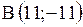
3.2.5. 1) 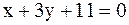 ; 2)
; 2)  .
.
3.2.6.  ;
;  .
.
3.2.7. 1)  ; 2)
; 2)  .
.
3.2.8. 5 ед. масштаба.
3.2.9.  .
.
3.2.10.  ,
,  ,
,
 ,
,  .
.
3.2.11.  ;
; 
 .
.
3.2.12. 1)  ; 2)
; 2)  ,
,  ; 3)
; 3)  ;
;
4)  ,
,  .
.
3.2.13.  ,
,  ,
,  .
.
3.2.14.  .
.
3.2.15.  .
.
3.2.16. 
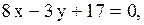

3.2.17. 

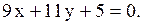
3.2.18.  .
.
3.2.19. 5.
3.2.20. 49.
3.2.21. Два квадрата:
1) 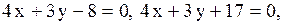

2) 
3.2.22. 
3.2.23. 
3.2.24.  .
.
3.2.25.  .
.
3.2.26. 2.
3.2.27. 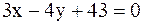 .
.
3.2.28. 16.
3.2.29. 1)  и 3; 2)
и 3; 2)  и
и  ; 3)
; 3)  ; 4)
; 4)  .
.
3.2.30.  . Указание. Воспользоваться свойством эллипса: произведение расстояний от фокусов до любой касательной к эллипсу равно квадрату малой полуоси.
. Указание. Воспользоваться свойством эллипса: произведение расстояний от фокусов до любой касательной к эллипсу равно квадрату малой полуоси.
3.2.31.  .
.
3.2.32. 1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ,
,  ; 5)
; 5)  ,
,  .
.
3.2.33.  .
.
3.2.34.  .
.
3.2.35.  .
.
3.2.36.  .
.
3.2.37. 1) парабола; 2) часть параболы, расположенная в четвертом координатном углу; 3) гипербола; 4) ветвь гиперболы, расположенная в нижней полуплоскости; 5) ветвь гиперболы, расположенная в левой полуплоскости; 6) половина эллипса, расположенная в левой полуплоскости; 7) и 8) эллипс; 9) гипербола; 10) правая ветвь гиперболы; 11) парабола.
3.2.38. 1) 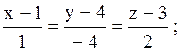 2)
2) 
3.2.39. 1) 
2) 
3.2.40. 1)  2)
2) 
3.2.41.
1) 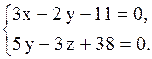
| 2) 
| 3)

|
3.2.42. 1)  2)
2) 
3.2.43. 1) 
2) 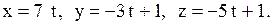
3.2.46.  .
.
3.2.47.  .
.
3.2.49.  .
.
3.2.50. 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
3.2.51. 6.
3.2.52.  .
.
3.2.53. 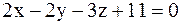 .
.
3.2.54.  .
.
3.2.55. 1)  ; 2)
; 2)  .
.
3.2.56.  ;
;  .
.
3.2.57.  или
или  .
.
3.2.58. 1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  .
.
3.2.59.  .
.
3.2.60.  .
.
3.2.61.  .
.
3.2.62.  .
.
3.2.63.  .
.
3.2.64. 1) эллипсоид; 2) однополостный гиперболоид; 3) конус; 4) двуполостный гиперболоид; 5) эллиптический параболоид; 6) конус; 7) однополостный гиперболоид; 8) двуполостный гиперболоид.
3.2.65.  ;
;  .
.
3.2.66. 1) 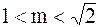 ; 2)
; 2)  .
.