Билет 1.
1. Прямая-это одно из основных понятий геометрии. Не имеет не конца не начала.
2. Отрезок-это часть прямой, состоящее из двух различных точек и всех точек, лежащих между ними.
3. Луч-это часть прямой, содержащая только одну точку.
4. Угол-это геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (вершины угла).
Билет 2.
1. Сме́жные углы́ — это пара углов, которые дополняют друг друга до 180 градусов. Два смежных угла имеют общую вершину и одну общую сторону, две другие (не общие) стороны образуют прямую линию. Для угла 135 градусов смежным является угол в 45 градусов. Для угла x градусов смежным является угол 180 - x градусов.
2. 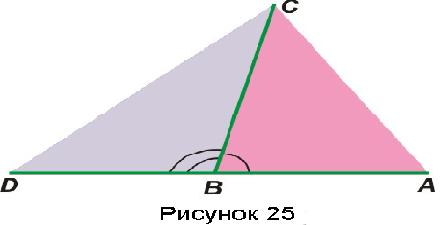 На рисунке 25 углы ABC и CBD смежные. У них сторона ВС общая, а стороны BA и BD являются продолжениями одна другой и дополняют до прямой.
На рисунке 25 углы ABC и CBD смежные. У них сторона ВС общая, а стороны BA и BD являются продолжениями одна другой и дополняют до прямой.
Теорема. Сумма смежных углов равна 180о.
Доказательство. Пусть ÐАВС и ÐCBD – данные смежные углы (Рис. 25). Так как лучи ВА и BD образуют развернутый угол, то ÐАВС+ÐCBD =180°.
Теорема доказана.
Можно найти величину одного из смежных углов, если известна величина другого угла. Например, ÐАВС =72°, величина смежного ему угла будет равна 180°- 72°=108°.
Каждое утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой, а сами рассуждения называются доказательством теоремы. Мы доказали первую теорему о смежных углах.
Билет 3.
1.  Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
На рисунке 26 углы ÐEOF и Ð AOC, а также углы ÐAOE и ÐCOF – вертикальные. Потому что сторона ОА является продолжением луча OF, а сторона OC является продолжением луча OE и дополняет до прямой.
Теорема. Вертикальные углы равны.
Доказательство. Пусть Ð1 и Ð2 – данные вертикальные углы (Рис. 27). Тогда Ð1 и Ð3 смежные, также Ð2 и Ð3 смежные углы. Отсюда из теоремы 1:
Ð 1+Ð3 = 180°
Ð2+Ð3 = 180°
Из этого: Ð1+Ð3=Ð2+Ð3. Из этого равенства получим Ð1=Ð2, т. е. вертикальные углы 1 и 2 равны.
Билет 4.
Если внутренние накрест лежащие углы равны, то прямые параллельны.
Доказательство
На основании теоремы 3.1 можно легко доказать еще несколько признаков параллельности.
Если соответственные углы равны, то прямые параллельны.
Если сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Из данного утверждения вытекает
Две прямые, перпендикулярные третьей, параллельны.
Билет 5.
1.Треугольник-это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти три точки.
2.  - тупоуголный
- тупоуголный  -остроугольный
-остроугольный
 -равносторонний -прямоугольный
-равносторонний -прямоугольный
-разносторонний треугольник
3.Равенство треугольников: 
Два треугольника называются равными (Δ A1B1C1 = Δ A2B2C2), если у них соответствующие стороны равны и соответствующие углы равны. A1B1=A2B2, B1C1=B2C2, C1A1=C2A2 и ∠ B1A1C1 = ∠ B2A2C2, ∠ A1B1C1 = ∠ A2B2C2, ∠ B1C1A1 = ∠ B2C2A2.
Билет 6.
|
Билет 7.
Теорема


Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
Доказательство.
Пусть у треугольников ABC и A1B1C1 ∠ A = ∠ A1, ∠ B = ∠ B1, AB = A1B1. Пусть A1B2C2 – треугольник, равный треугольнику ABC. Вершина B2 расположена на луче A1B1, а вершина С2 в той же полуплоскости относительно прямой A1B1, где лежит вершина С1. Так как A1B2 = A1B1, то вершина B2 совпадает с вершиной B1. Так как ∠ B1A1C2 = ∠ B1A1C1 и ∠ A1B1C2 = ∠ A1B1C1, то луч A1C2 совпадает с лучом A1C1, а луч B1C2 совпадает с лучом B1C1. Отсюда следует, что вершина С2 совпадает с вершиной С1. Треугольник A1B1C1 совпадает с треугольником A1B2C2, а значит, равен треугольнику ABC. Теорема доказана.
Билет 8
|
Билет9.
Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.
Теорема.
Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.
Доказательство


Пусть a – данная прямая и не лежащая на этой прямой точка A. Проведем через какую-нибудь точку прямой a перпендикулярную ей прямую с. Прямая с пересекает прямую a в точке С. Теперь проведем параллельно прямой с прямую b, так чтобы что бы прямая b проходила через точку A. Тогда прямая b ⊥ a, так как b || с и с ⊥ a.
Значит отрезок AB ⊥ a.
Теперь докажем единственность перпендикуляра AB.
Допустим, существует еще перпендикуляр, проходящий через точку A к прямой a.
Тогда у треугольника ABD будет два угла по 90 °. А этого не может быть, так как сумма всех углов в треугольнике 180 °. Теорема доказана.
Билет 10.
Медиа́на треуго́льника -отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны, а также прямая, содержащая этот отрезок.
Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Высота треугольника — перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Свойства: В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке, высоты или их продолжения так же пересекаются в одной точке.
Билет 11.
Равнобедренный треугольник — это треугольник, в котором две стороны равны. Равные стороны называются боковыми, а последняя — основанием.
|
Билет12.
Биссектриса угла, опущенная из вершины равнобедренного треугольника является и медианой и высотой данного треугольника. Получается:
биссектриса опущенная к основанию делит его (основание) на две равные части...
Билет 13.
Окружность-это множество точек плоскости расположенных на данном расстояние от данной точки.
т. О-центр окружности.
R. - радиус
D-диаметр (самая большая хорда)
Хорда-это отрезок, концы которого лежат на окружности.
Билет 14.
Две прямые называются параллельными, если они не пересекаются.
Два отрезка называются параллельными, если лежат на параллельных прямых.
1 признак параллельности прямых:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Дано:
А,В-прямые
С- секущая
Угол 1
Угол 2 доказательство:
Доказать: 1)Проведем прямую, 2)т.к ОВ=ОА(по построению)
А параллельна В? Угол 1 = углу 2 (по условию)
Угол КОА= углу НОВ т.к они вертикальные
КОА = НОВ по 2 признаку, из этого вытекает
Угол НОВ = угол ОКА=90гр.
т.е А перпендикулярна КН, а В перпендикулярна КН
вытекает А параллельна В ч.т.д.
Билет 15.
Если при пересечении двух прямых третьей соответственные углы равны, то прямые параллельны.
Доказательство:
Воспользуйтесь рисунком и убедитесь, что из равенства соответственных углов следует равенство внутренних накрест лежащих углов (используйте свойство вертикальных углов) и по первому признаку параллельности прямые параллельны.
Билет 16.
Если при пересечении двух прямых третьей сумма односторонних (внутренних или внешних) углов равна  , то прямые параллельны. Доказательство:
, то прямые параллельны. Доказательство:
Доказывается аналогично второму признаку параллельности (используйте свойство смежных углов).
Билет 17.
1)Если две прямые пересечены секущей, то накрест лежащие углы равны.
2)Если прямая перпендикулярна к одной из двух параллельных, то она перпендикулярна к другой.
Билет 19.
Второе свойство параллельных прямых.

 Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Доказательство. Пусть у треугольников ABC и A1B1C1 ∠ A = ∠ A1, AB = A1B1, AC = A1C1. Пусть есть треугольник A1B2C2 – треугольник равный треугольнику ABC, с вершиной B2, лежащей на луче A1B1, и вершиной С2 в той же полуплоскости относительно прямой A1B1, где лежит вершина С1.
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Доказательство. Пусть у треугольников ABC и A1B1C1 ∠ A = ∠ A1, AB = A1B1, AC = A1C1. Пусть есть треугольник A1B2C2 – треугольник равный треугольнику ABC, с вершиной B2, лежащей на луче A1B1, и вершиной С2 в той же полуплоскости относительно прямой A1B1, где лежит вершина С1. 

 Так как A1B1=A1B2, то вершины B1 и B2 совпадают. Так как ∠ B1A1C1 = ∠ B2A1C2, то луч A1C1 совпадает с лучом A1C2. Так как A1C1 = A1C2, то точка С1 совпадает с точкой С2. Следовательно, треугольник A1B1C1 совпадает с треугольником A1B2C2, а значит, равен треугольнику ABC. Теорема доказана.
Так как A1B1=A1B2, то вершины B1 и B2 совпадают. Так как ∠ B1A1C1 = ∠ B2A1C2, то луч A1C1 совпадает с лучом A1C2. Так как A1C1 = A1C2, то точка С1 совпадает с точкой С2. Следовательно, треугольник A1B1C1 совпадает с треугольником A1B2C2, а значит, равен треугольнику ABC. Теорема доказана.
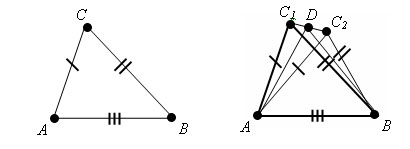
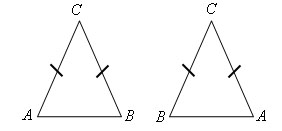 Треугольник ACB равен треугольнику BCA по первому признаку равенства треугольников. AC = BC, CB = CA, ∠ C = ∠ C. Следовательно ∠ A = ∠ B. Теорема доказана.
Треугольник ACB равен треугольнику BCA по первому признаку равенства треугольников. AC = BC, CB = CA, ∠ C = ∠ C. Следовательно ∠ A = ∠ B. Теорема доказана.