Digital Devices. Lecture 1.4.- 1.5.Basic correlation Boolean Algebra and their application.
Boolean algebra is mathematics of logic. It is one of the most basic tools available to the logic designer and thus can be effectively used for simplification of complex logic expressions.
1.1 Variables, Literals and Terms in Boolean Expressions.
Variables are the different symbols in a Boolean expression. They may take on the value ‘0’ or ‘1’. For instance, in expression (1.1), A, B and C are the three variables. In expression (1.2), P, Q, R and S are the variables:
A+A×B+A× 
+ 
B×C (1.1)
(
+Q)×(R+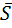 
)×(Q+R+P) (1.2)
The complement of a variable is not considered as a separate variable. Each occurrence of a variable or its complement is called a literal. In expressions (1.1) and (1.2) there are eight and seven literals respectively. A term is the expression formed by literals and operations at one level. Expression (1.1) has four terms.
1 .2 Equivalent and Complement of Boolean Expressions
Two given Boolean expressions are said to be equivalent if one of them equals ‘1’ only when the other equals ‘1’ and also one equals ‘0’ only when the other equals ‘0’. They are said to be the complement of each other if one expression equals ‘1’ only when the other equals ‘0’, and vice versa. The complement of a given Boolean expression is obtained by complementing each literal, changing all ‘.’ to ‘+’ and all ‘+’ to ‘.’, all 0s to 1s and all 1s to 0s. The examples below give some Boolean expressions and their complements:
Given Boolean expression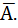 
B + A. 
(1.3)
Corresponding complement (A+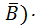 
(
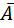+ B) (1.4)
Given Boolean expression (A+B)×( +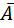 
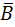) (1.5) Corresponding complement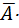 
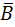+A×B (1.6)
The ‘.’ sign is usually omitted in writing Boolean expressions and is implied merely by writing the literals in juxtaposition. For instance, A.B would normally be written as AB.
Dual of a Boolean Expression.
The dual of a Boolean expression is obtained by replacing all ‘.’ operations with ‘+’ operations, all ‘+’ operations with ‘.’ operations, all 0s with 1s and all 1s with 0s and leaving all literals unchanged. The examples below give some Boolean expressions and the corresponding dual expressions:
Given Boolean expression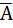 
×B + A× (1.7)
Corresponding dual (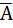 + B) × (A + ) (1.8)
Given Boolean expression (A + B)× ( +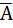 
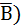(1.9)
Corresponding dual A×B + 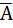× (1.10)
Duals of Boolean expressions are mainly of interest in the study of Boolean postulates and theorems.
Example 1. Find (a) the dual of A× 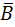+ B× 
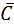+ C×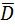 
and (b) complement
Solution. (a) The dual (a) (A + 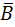)×(B + 
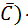(C+ )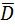
(b) The complement (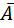 + B)×(
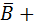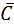C)×( + D).
Postulates of Boolean Algebra.
The following are the important postulates of Boolean algebra:
1. 1×1 = 1, Æ +Æ =Æ.
2. 1× Æ = Æ × 1 =Æ, Æ + 1 = 1 +Æ = 1.
3. Æ × Æ =Æ, 1 + 1 = 1.
4. 
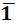= Æ 
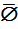= 1.
Many theorems of Boolean Algebra are based on these postulates, which can be used to simplify Boolean expression. Postulates describes function AND and OR gates.
3. Theorem of Boolean Algebra. The theorems of Boolean algebra can be used to simplify many a complex Boolean expression and also to transform the given expression into a more useful and meaningful equivalent expression. The theorems are presented as pairs, with the two theorems in a given pair being the dual of each other. These theorems can be very easily verified by the method of ‘perfect induction’. According to this method, the validity of the expression is tested for all possible combinations of values of the variables involved. Important point is that, if a given expression is valid, its dual will also be valid. Therefore, only one of the theorems in a given pair will be illustrated with a proof. Proof of the other being its dual is implied.
3.1. Theorem 1 (Operating with Æ and «1») (1., 2., 4. - законы одинарных элементов или одной переменной и константы)
(a) Æ × X = Æ (b-dual) 1 + X = 1 (3.1.)
(a) Æ×X = Æ irrespective of the value of X, and hence the proof.
(b) 1 + X = 1 follow from postulate 3.1, or as dual expression.
X is not necessarily a single variable – it could be a term or even a large Boolean expression. For example, Æ×(A×B + B×C + C×D) = Æ; 1 + (A×B + B×C + C×D) = 1, where A,B and C are Boolean variable.
3.2. Theorem 2 (Named as 1-th).
(a) 1×X = X (b) Æ + X = X (3.2.)
· For X =Æ, LHS = 1×Æ = Æ = RHS. Theorem 2 (as 1) can be proved by substituting all possible values of X, that is, Æ and 1, into the given expression and checking whether the LHS equals the RHS:
· For X =Æ, LHS = 1×Æ = Æ = RHS
· For X = 1, LHS = 1×1 = 1 = RHL.
Where X could be variable, a term or a large expression.
1×(Boolean expression)=(Boolean expression) and
Æ + (Boolean expression)=(Boolean expression).
3.3. Theorem 3 (Idempotent or Identity Laws) (тавтологии или многократного повторения).
(a) X×X×X× …×X = X (b) X + X + X+…+X = X (3.3.)
Theorem 3(a) is a direct outcome of AND gate operation. Let`s apply Th3 to simplify the following Boolean expression:
(A× × + C×C)×(A× × 
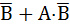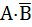+ C×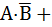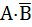C) = (
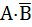+ C)×(
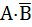+ C) =
( +C)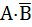× ( +C) = +C.
3.4. Theorem 4 (Complementation Law) (Законы дополнительных элементов).
(a) X× 
= Æ (b) X + 
= 1 (3.4.)
* For X = Æ,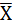 
= 1. Therefore, X× 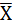= Æ×1 = Æ.
* For X = 1, 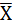= Æ. Therefore, X× 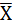= 1×Æ = Æ.
Hence, theorem 4(a) is proved. Since theorem 4(b) is dual 4(a), its proof is implied.
Example 4.1. Simplify the following:
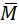[1 + L×M + L× 
+ 
M]×[(L + )×(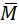
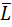× M) + 
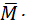(L + M)]
Solution: We know (Th1a) that (1 + Boolean expression) = 1;
also, (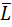 × M) is complement of (L + 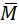) therefore according Th3a their product equal Æ and correspondingly 
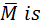complement of (L + M) and their product (Th3a) equal Æ; result 1×(Æ + Æ)=1.Æ=Æ.
3.5. Theorem 5 (Commutative Laws) (Переместительный- коммутативный законы).
(a) X + Y = Y + X (b) X×Y = Y×X (3.5.)
Theorem 5 implies that the order in which variables are added or ORed (multiply or ANDed) is immaterial.
3.6. Theorem 6 (Associative Laws) (Ассоциативный-сочетательности).
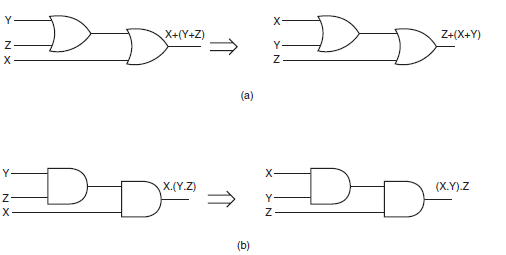
(a) X + (Y + Z) = Y + (Z + X) = Z + (X + Y) (3.6.)
(b) X×(Y×Z) = Y×(Z×X) = Z×(X×Y)
Theorem 6(a) and (b) are further illustrated by the logic diagrams.
