Федотов В.В., 4 курс, направление ГМУ, гр. ГЗВО-15
Научный руководитель – Ю.Н. Арсеньев, д.т.н., профессор
Российская академия народного хозяйства и государственной службы (РАНХиГС) при Президенте РФ
Аннотация: В статье рассматривается актуальная для развивающейся экономики Российской Федерации задача формирования и эффективного управления портфелем ценных бумаг. Для ее решения применяется активная стратегия, подразумевающая изменение структуры портфеля. Доли активов включаются в портфель по методу «Квази – Шарпа». Данная модель используется на неустойчивых фондовых рынках для эффективного управления активами. Исследования проводятся на примере доходности крупных российских компаний. Модель «Квази − Шарпа» соединяет доходность ценной бумаги с доходностью единичного портфеля и риском этой ценной бумаги с помощью функции линейной регрессии. Риск в данном методе измеряется с помощью коэффициента бета β, который характеризуется степенью чувствительности к изменению доходности единичного портфеля.
Ключевые слова: управление портфелем ценных бумаг, эффективный портфель, ожидаемый доход, доходность, заданный риск, инвестиции, ценные бумаги, модель Квази − Шарпа.
Статья посвящена актуальной для развивающейся экономики Российской Федерации проблеме формирования и управления портфелем ценных бумаг. Кризис 2008 года и последовавший за ним период стагнации в экономике России показали, что необходимо не только приобретать акции, но и эффективно ими управлять.
Сущность портфельного инвестирования подразумевает распределение инвестиционного потенциала между различными группами активов. В зависимости от того, какие цели и задачи первоначально стоят при создании того или иного портфеля, берется определенное процентное соотношение между различными типами активов, формирующими портфель инвестора. Главная задача инвестора учесть потребности и составить портфель активов, включающий в себя разумный риск и приемлемую доходность [1−3].
Для эффективной работы на нестабильных фондовых рынках была предложена новая модель формирования инвестиционного портфеля, которая получила название модель «Квази- Шарпа». Эта модель основана на взаимосвязи доходности каждой ценной бумаги из всего множества N ценных бумаг с доходностью единичного портфеля этих бумаг.
Модель «Квази - Шарпа» соединяет доходность ценной бумаги с доходностью единичного портфеля и риском этой ценной бумаги с помощью функции линейной регрессии. Формула доходности ценной бумаги следующая:
Ri = R¯i+ þi(Rcp — R¯cp);
Ri- доходность ценной бумаги;
Rsp- доходность единичного портфеля;
βi- коэффициент чувствительности к изменению доходности ценной бумаги, коэффициент регрессии в уравнении доходности;
R¯i-средняя доходность ценной бумаги;
R¯cp- средняя доходность единичного портфеля
Проведем исследование на примере котировок по акциям за период 14.09.2017 по 14.09.2018 таких крупных российских компаний как ПАО «Газпром» (GAZP), ПАО «Татнефть» (TATN), ПАО Лукойл (LKOH), ОАО ГМК «Норильский никель» (GMKN) и ПАО «Корпорация «Иркут» (https://ru.investing.com) [4]. С помощью программного обеспечения Microsoft Excel рассчитаем доходность акций каждой компании.
Таблица № 1
Месячные данные по стоимости акций компаний с 14.09.2017 по 14.09.2018.
| Газпром (GAZP) | Татнефть (TATN) | Лукойл (LKOH) | Норникель (GMKN) | Иркут (IRKT) | |
| окт.17 | 125,90 | 436,00 | 3 096,00 | 10 592,00 | 15,42 |
| ноя.17 | 132,15 | 456,70 | 3 292,50 | 9 876,00 | 14,94 |
| дек.17 | 130,50 | 478,80 | 3 334,50 | 10 850,00 | 14,27 |
| янв.18 | 143,36 | 565,20 | 3 728,00 | 11 608,00 | 14,87 |
| фев.18 | 143,16 | 594,00 | 3 776,50 | 11 159,00 | 15,00 |
| мар.18 | 142,33 | 611,60 | 3 961,00 | 10 760,00 | 14,45 |
| апр.18 | 145,93 | 671,05 | 4 156,50 | 10 814,00 | 13,95 |
| май.18 | 145,00 | 666,50 | 4 209,00 | 11 111,00 | 15,35 |
| июн.18 | 141,01 | 675,95 | 4 350,00 | 11 399,00 | 16,80 |
| июл.18 | 143,79 | 721,40 | 4 451,50 | 10 882,00 | 25,95 |
| авг.18 | 149,95 | 783,10 | 4 700,50 | 11 220,00 | 31,15 |
| сен.18 | 152,15 | 794,00 | 4 604,00 | 11 525,00 | 58,30 |
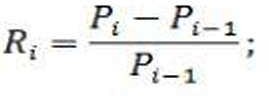
Рассчитаем доходности этих акций по следующей формуле:
где:
Rj- текущая доходность акции; Pi- текущая стоимость акции;
Рi-1 - стоимость акции в предыдущем периоде.
Следующим этапом, для каждой акции рассчитаем среднее значение доходности за весь год, то есть за все временные отрезки. Формула для расчета следующая:
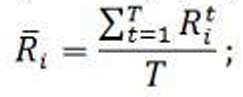
Где:
Rit- доходность i-ой акции за период t;
Т- рассматриваемое количество временных периодов (в нашем случае 12).
В Таблице 2 показан расчет доходности по акциям и средне значение доходности по акциям за весь год. Каждый столбец представляет месячные доходности каждой акции.
Таблица № 2
Месячная доходность по акциям российских компаний за год
| Доходность | |||||
| GAZP | TATN | LKOH | GMKN | IRKT | |
| 0,049643 | 0,04747706 | 0,06346899 | -0,0676 | -0,03113 | |
| -0,01249 | 0,04839063 | 0,01275626 | 0,098623 | -0,04485 | |
| 0,098544 | 0,18045113 | 0,1180087 | 0,069862 | 0,042046 | |
| -0,0014 | 0,05095541 | 0,01300966 | -0,03868 | 0,008742 | |
| -0,0058 | 0,02962963 | 0,04885476 | -0,03576 | -0,03667 | |
| 0,025293 | 0,09720405 | 0,04935622 | 0,005019 | -0,0346 | |
| -0,00637 | -0,00678042 | 0,01263082 | 0,027464 | 0,100358 | |
| -0,02752 | 0,01417854 | 0,03349964 | 0,02592 | 0,094463 | |
| 0,019715 | 0,0672387 | 0,02333333 | -0,04535 | 0,544643 | |
| 0,04284 | 0,08552814 | 0,0559362 | 0,03106 | 0,200385 | |
| 0,014672 | 0,01391904 | -0,0205297 | 0,027184 | 0,871589 | |
| Ср. доходность | 0,017922 | 0,05710836 | 0,03730226 | 0,008886 | 0,155908 |
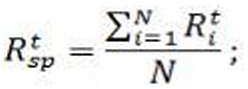
Сделав необходимые расчеты, рассчитаем доходности единичного портфеля и его среднюю доходность за все периоды (Таблица №3). Доходность единично портфеля представляет собой доходность портфеля составленного из используемых акций, взятых в равных пропорциях.
Где:
| cp |
| cp |
Средняя доходность единичного портфеля за все периоды рассчитывается так:
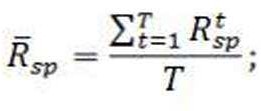
Где:
R¯cp- средняя доходность единичного портфеля;
Т- рассматриваемое количество временных периодов;
| cp |
Таблица № 3
Расчет доходности единичного портфеля
| Доходность ЕП | |
| 0,012372408 | |
| 0,020487591 | |
| 0,101782378 | |
| 0,006526439 | |
| 5,28243E-05 | |
| 0,028454024 | |
| 0,025460061 | |
| 0,028108749 | |
| 0,12191499 | |
| 0,083150083 | |
| 0,18136671 | |
| Ср. доходность ЕП | 0,055425114 |
Далее рассчитаем чувствительность изменения доходности акции от изменения доходности единичного портфеля (Таблица 3). Чувствительность показывает коэффициент бета (β). Формула его вычисления следующая:
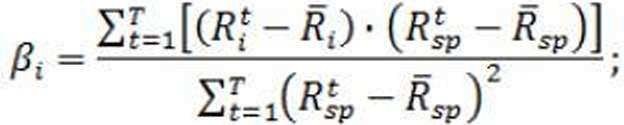
Коэффициент бета (β) будет рассчитан как отношение числителей к знаменателю.
Таблица № 4
Расчет чувствительности (Коэффициент β)
| Знаминатель (β) | Числ. 1 | Числ. 2 | Числ. 3 | Числ. 4 | Числ. 5 | |
| GAZP | TATN | LKOH | GMKN | IRKT | ||
| 0,001853536 | -0,00136567 | 0,000415 | -0,00113 | 0,003293 | 0,008052 | |
| 0,001220631 | 0,001062361 | 0,000305 | 0,000858 | -0,00314 | 0,007014 | |
| 0,002148996 | 0,003737435 | 0,005718 | 0,003741 | 0,002827 | -0,00528 | |
| 0,00239108 | 0,000944562 | 0,000301 | 0,001188 | 0,002326 | 0,007196 | |
| 0,00306609 | 0,001313394 | 0,001522 | -0,00064 | 0,002472 | 0,010663 | |
| 0,00072744 | -0,00019882 | -0,00108 | -0,00033 | 0,000104 | 0,005138 | |
| 0,000897904 | 0,000727987 | 0,001914 | 0,000739 | -0,00056 | 0,001665 | |
| 0,000746184 | 0,001241225 | 0,001173 | 0,000104 | -0,00047 | 0,001678 | |
| 0,004420904 | 0,000119235 | 0,000674 | -0,00093 | -0,00361 | 0,025847 | |
| 0,000768674 | 0,000690868 | 0,000788 | 0,000517 | 0,000615 | 0,001233 | |
| 0,015861286 | -0,00040932 | -0,00544 | -0,00728 | 0,002304 | 0,090134 | |
| Ср. значение | 0,034102724 | 0,007863253 | 0,006287 | -0,00316 | 0,006177 | 0,153343 |
| Бета (β) = | 0,230575509 | 0,184365 | -0,09257 | 0,181136 | 4,496498 |
Следующим этапом рассчитаем остаточный риск, который представляет собой степень разброса доходности ценной бумаги относительно линии регрессии. Формула расчета остаточного риска следующая:
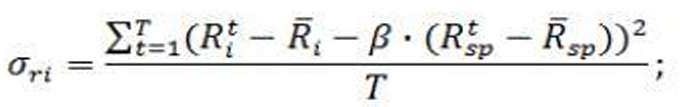
Также, при формировании инвестиционного портфеля из этих акций нам еще потребуется рассчитать риск единичного портфеля:

Таблица № 5
Расчет остаточного риска и риска единичного портфеля
| Остаточный риск | |||||
| GAZP | TATN | LKOH | GMKN | IRKT | |
| 0,001026 | 9,42402E-05 | 0,000679 | 0,005941 | 0,049838 | |
| 0,00094 | 7,6981E-05 | 0,000599 | 0,008155 | 0,053959 | |
| 0,006362 | 0,014954502 | 0,00657 | 0,003656 | 0,008123 | |
| 0,000382 | 3,85444E-05 | 0,000585 | 0,002303 | 0,032228 | |
| 0,000577 | 0,000770576 | 0,000132 | 0,002033 | 0,057851 | |
| 5,5E-05 | 0,001623693 | 0,000145 | 1,51E-05 | 0,045631 | |
| 0,000598 | 0,004127 | 0,000605 | 0,000349 | 0,003973 | |
| 0,002091 | 0,001861579 | 1,44E-05 | 0,000293 | 0,00476 | |
| 3,12E-06 | 0,000100123 | 0,000198 | 0,002872 | 0,074264 | |
| 0,000613 | 0,000799448 | 0,000349 | 0,000487 | 0,001516 | |
| 9,96E-06 | 0,0017797 | 0,003423 | 0,00032 | 0,096344 | |
| Ср. значение | 0,001151 | 0,002384217 | 0,001209 | 0,002402 | 0,038953 |
| Риск единичного порфеля = | 0,053309414 |
Итак, систематизируем полученные данные в таблицу № 6.
Таблица № 6
| Название | Коэффициент (β) | Средняя доходность | Остаточный риск |
| Газпром (GAZP) | 0,231 | 1,79% | 0,12% |
| Татнефть (TATN) | 0,184 | 5,71% | 0,24% |
| Лукойл (LKOH) | -0,093 | 3,73% | 0,12% |
| Норникель (GMKN) | 0,181 | 0,89% | 0,24% |
| Иркут (IRKT) | 4,496 | 15,59% | 3,90% |
Очевидно, что наивысшее изменение доходности ценной бумаги от колебания доходности единичного портфеля у компании ПАО «Корпорация «Иркут», а наименьшая зависимость у ПАО «Лукойл». Наибольшая средняя доходность компании ПАО «Корпорация «Иркут» характеризуется большим остаточным риском в сравнение с другими корпорациями.
Для расчета долей в инвестиционном портфеле воспользуемся надстройкой «Поиск решений» в Microsoft Excel. Необходимо максимизировать доходность инвестиционного портфеля с ограничением на риск. Сделаем расчеты в трёх вариантах событий:
1) при максимальном риске в 1%;
2) при максимальном риске в 5%;
3) при максимальном риске в 10%.
Таблица № 7
Результаты долей инвестирования в портфеле при максимальном риске в 1%
| Название | Доходность | Бета (β) | Остаточный риск | Риск ЕП | Rsp-<Rsp> | Доля (W) | R*W | β*W | (β*W)^2 | σ^2*W^2 |
| Газпром (GAZP) | 1,79% | 0,231 | 0,12% | |||||||
| Татнефть (TATN) | 5,71% | 0,184 | 0,24% | 0,907236 | 0,05181 | 0,16726 | 0,02798 | 4,68E-06 | ||
| Лукойл (LKOH) | 3,73% | -0,093 | 0,12% | 5,33% | 0,055 | 0,07646 | 0,00285 | -0,0071 | 5E-05 | 8,54E-09 |
| Норникель (GMKN) | 0,89% | 0,181 | 0,24% | |||||||
| Иркут (IRKT) | 15,59% | 4,496 | 3,90% | 0,016305 | 0,00254 | 0,07331 | 0,00538 | 4,03E-07 | ||
| Cумма W = | 0,0572 | 0,2335 | 0,0334 | 5,09E-06 | ||||||
| Доходность портфеля = | 7,01% | |||||||||
| Риск инвест. портфеля = | 1% |
При максимальном риске в 1%, мы получили следующее соотношение весов акций в инвестиционном портфеле. Доля акций ПАО «Газпром» (GAZP) составляет 0%, доля акций ПАО «Татнефть» (TATN) составляет 90,7%, доля акций ПАО «Лукойл» (LKOH) составляет 7,7%, доля акций ОАО ГМК «Норильский никель» (GMKN) составляет 0% и доля акций ПАО «Корпорация «Иркут» составляет 1,6%. Доходность такой структуры портфеля составила 7,01%.
Таблица №8
Результаты долей инвестирования в портфеле при максимальном риске в 5%
| Название | Доходность | Бета (β) | Остаточный риск | Риск ЕП | Rsp-<Rsp> | Доля (W) | R*W | β*W | (β*W)^2 | σ^2*W^2 | ||||||||||
| Газпром (GAZP) | 1,79% | 0,231 | 0,12% | |||||||||||||||||
| Татнефть (TATN) | 5,71% | 0,184 | 0,24% | 0,796803 | 0,0455 | 0,1469 | 0,02158 | 3,61E-06 | ||||||||||||
| Лукойл (LKOH) | 3,73% | -0,093 | 0,12% | 5,33% | 0,055 | |||||||||||||||
| Норникель (GMKN) | 0,89% | 0,181 | 0,24% | |||||||||||||||||
| Иркут (IRKT) | 15,59% | 4,496 | 3,90% | 0,203197 | 0,03168 | 0,91368 | 0,8348 | 6,27E-05 | ||||||||||||
| Cумма W = | 0,07718 | 1,06058 | 0,85638 | 6,63E-05 | ||||||||||||||||
| Доходность портфеля = | 13,60% | |||||||||||||||||||
| Риск инвест. портфеля = | 5% | |||||||||||||||||||
При максимальном риске в 5%, мы получили следующее соотношение весов акций в инвестиционном портфеле. Доля акций ПАО «Газпром» (GAZP) составляет 0%, доля акций ПАО «Татнефть» (TATN) составляет 79,7%, доля акций ПАО «Лукойл» (LKOH) составляет 0%, доля акций ОАО ГМК «Норильский никель» (GMKN) составляет 0% и доля акций ПАО «Корпорация «Иркут» составляет 20,3%. Доходность такой структуры портфеля составила 13,60%.
Таблица №9
Результаты долей инвестирования в портфеле при максимальном риске в 10%
| Название | Доходность | Бета (β) | Остаточный риск | Риск ЕП | Rsp-<Rsp> | Доля (W) | R*W | β*W | (β*W)^2 | σ^2*W^2 |
| Газпром (GAZP) | 1,79% | 0,231 | 0,12% | |||||||
| Татнефть (TATN) | 5,71% | 0,184 | 0,24% | 0,588954 | 0,03363 | 0,10858 | 0,01179 | 1,97E-06 | ||
| Лукойл (LKOH) | 3,73% | -0,093 | 0,12% | 5,33% | 0,055 | |||||
| Норникель (GMKN) | 0,89% | 0,181 | 0,24% | |||||||
| Иркут (IRKT) | 15,59% | 4,496 | 3,90% | 0,411046 | 0,06409 | 1,84827 | 3,41608 | 0,000256 | ||
| Cумма W = | 0,09772 | 1,95685 | 3,42788 | 0,000258 | ||||||
| Доходность портфеля = | 20,62% | |||||||||
| Риск инвест. портфеля = | 10% |
При максимальном риске в 10%, мы получили следующее соотношение весов акций в инвестиционном портфеле. Доля акций ПАО «Газпром» (GAZP) составляет 0%, доля акций ПАО «Татнефть» (TATN) составляет 58,9%, доля акций ПАО «Лукойл» (LKOH) составляет 0%, доля акций ОАО ГМК «Норильский никель» (GMKN) составляет 0% и доля акций ПАО «Корпорация «Иркут» составляет 41,1%. Доходность такой структуры портфеля составила 20,62%.
Таблица № 10
Соотношение долей акций в портфеле при заданном уровне максимального риска и их доходность
| Название | Соотношение долей акций в портфеле | ||
| 1% | 5% | 10% | |
| Газпром (GAZP) | 0,0% | 0,0% | 0,0% |
| Татнефть (TATN) | 90,7% | 79,7% | 58,9% |
| Лукойл (LKOH) | 7,7% | 0,0% | 0,0% |
| Норникель (GMKN) | 0,0% | 0,0% | 0,0% |
| Иркут (IRKT) | 1,6% | 20,3% | 41,1% |
| Доходность портфеля | 7,01% | 13,60% | 20,62% |
Отметим, что чем выше инвестиционный риск, тем более доходный портфель ценных бумаг инвестора. Диверсификация портфеля ценных бумаг позволяет снизить инвестиционный риск, но доходность данной структуры будет существенно ниже.
Модель «Квази-Шарпа » рационально использовать при рассмотрении небольшого числа ценных бумаг, принадлежащих одной или нескольким отраслям. С помощью этой модели хорошо поддерживать оптимальную структуру уже созданного инвестиционного портфеля. Недостатком этой модели можно считать не учет глобальных тенденций, которые влияют на доходность портфеля.
Литература
1. Сенников А.С., Клянина Л.Н. Применение эконометрических моделей для формирования эффективных портфелей российских ценных бумаг без ограничения прав продажи // Инженерный вестник Дона. 2016. №2 URL: ivdon.ru/ru/magazine/archive/n2y2016/3641
2. Gitman L.J., Joehnk M.D. Fundamentals of investing. Boston: Pearson Addison-Wesley, 2008. 681 p.
3. Семенкова Е.В. Операции с ценными бумагами. М.: Перспектива, 2004. 328 с.
4. Investing.com: финансовый портал. 2007. URL: ru.investing.com/equities/ (дата обращения: 16.09.2018).
5. Килячков А.А., Чалдаева Л.А. Рынок ценных бумаг и биржевое дело. М.: Норма-Юристъ, 2001. 687 с.
6. Sharpe W.F., Alexander G.J., Bailey J.V. Investments. 5th edition. Prentice Hall, 1994. 900 p.
7. Krebs Y. Consumer portfolio // Forbes. 2007. №9. p. 44 URL:forbes.ru/forbes/issue/2007-09/18327-potrebitelskii-portfel
8. Колесов П. Ф. Новый концептуальный подход оценки эффективности инвестиционных операций коммерческих банков с ценными бумагами // Инженерный вестник Дона. 2011. № 3 URL: ivdon.ru/ru/magazine/archive/n3y2011/514
9. Коссов В.В., Лившиц В.Н., Шахназаров А.Г. Методические рекомендации по оценке эффективности инвестиционных проектов. 2-е изд. М.: Экономика. 2000. 421 с.