Лекция № 1. Характеристика электронных программных средств обучения математике как средства формирования пространственных представлений школьников (психолого-педагогические и методические аспекты)
Краткое содержание
На лекции рассматриваются основы развития пространственного мышления школьников и выделяются те аспекты проблемы, которые могут быть оптимизированы с помощью электронных программных средств. Приводятся соответствующие примеры.
Формирование пространственных представлений осуществляется через овладение учащимися несколькими группами умений:
– умение представить по чертежу целостный образ геометрической фигуры, взаимное расположение ее элементов;
– умение мысленно изменить положение фигуры – посмотреть с другой стороны;
– умение мысленно расчленить фигуру, составить из нее новый объект;
– умение изобразить фигуру на чертеже, адекватно отразив имеющиеся отношения;
– умение представить фигуру на основе ее словесного описания и т.д.
Формирование перечисленных умений осуществляется в несколько этапов.
На I этапе на наглядной основе формируются предпосылки для создания целостного образа фигуры с выделением ее существенных признаков. На данном этапе учитель должен широко использовать модели, реальные объекты окружающего мира. После этого строится чертеж, который закрепляет рассмотрение соответствующей геометрической конфигурации.
В конце I этапа и на II у школьников формируются образы фигур и их комбинаций, которые они могут представить себе в почти неизмененных условиях.
Схема формирования пространственных представлений на I и II этапе следующая:
Модель чертеж представление
|
|
На этом этапе с помощью электронных программных средств демонстрируются подвижные чертежи каркасных моделей пространственных тел, а также модели самих тел и анализируется вопрос о том, какой чертёж будет давать более полное представление об объекте. Для этого могут быть использованы материалы готовых программных продуктов «Открытая стереометрия» или «Живая математика», «Математический конструктор», «GeoGebra» и др. Приводятся примеры.
На II этапе роль моделей несколько уменьшается, т. к. в противном случае у школьников будет тормозиться развитие способностей мысленно представлять себе особенности расположения фигуры и ее элементов.
При построении чертежа на данных этапах учителю не следует сразу демонстрировать готовый чертеж, а стараться его выполнять постепенно вместе с учащимися с целью поэтапного восприятия пространственных образов.
С помощью электронных программных средств демонстрируется процесс выполнения чертежа в динамике, самостоятельное выполнение чертежей учащимися с использованием соответствующих программ.
III этап: – овладение умением оперировать образами в измененных условиях. Школьники сначала работают с основным чертежом, который, однако, часто не дает возможность увидеть особенности расположения фигуры с разных позиций. Поэтому чертеж, как правило, должен подкрепляться рассмотрением соответствующей модели. Демонстрация сопровождается специально подобранными вопросами.
Например: Какие фигуры могут получиться при пересечении тетраэдра плоскости? Покажите на модели и чертеже различные случаи. Ответ обоснуйте.
|
|
Схема формирования пространственных представлений на III этапе:
чертеж модель представление.
Наиболее эффективными средствами развития пространственных представлений учащихся, как известно, являются: демонстрирование фигур, сравнение положений геометрических фигур относительно друг друга, моделирование, грамотное изображение фигур, чтение чертежа. Эти средства приводят к наилучшим результатам, если они используются систематически и в комплексе.
Для формирования пространственного воображения учащихся при изучении геометрии интерактивные задания и трехмерные модели играют особую роль. Используя данные объекты на любом этапе урока, учащиеся могут не только изучить пространственную структуру объемного (трехмерного) объекта, но и, меняя режим отображения объекта, выбрать, например, оптимальное изображение для решения задачи или оптимальное размещение данного трехмерного объекта для изображения его на плоскости.
Решение геометрической задачи на первом этапе – это её представление в пространстве, на втором – оптимальное изображение плоскостной или пространственной фигуры на плоскости. И насколько верно будут выполнены задачи первых двух этапов, настолько быстро и правильно будет решена вся задача. Показать правильный чертеж к задаче - почти все равно, что сразу объяснить ее решение, при этом формируется пространственное воображение, а так же умение, вообще, «видеть» чертеж.
Важнейшей отличительной чертой трехмерных моделей является то, что при работе с ними можно в любой момент произвольно изменить ракурс изображения. Очевидно, что работа в такой среде отлично развивает пространственное воображение. Появляется возможность по-новому ставить и решать задачи на построение в пространстве, причем проверить правильность решения можно, взглянув на конструкцию с разных сторон.
|
|
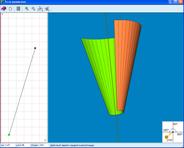
Конструктор тела вращения в ИИСС «Геометрическое конструирование на плоскости и в пространстве»
Для развития пространственного воображения на этапе закрепления немаловажную роль играют и иллюстрации. Например, для закрепления понятий объемов сложных пространственных объектов, определений многогранников (выпуклых, невыпуклых), видов сечений (по готовым чертежам).
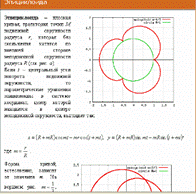
Словарная статья «Эпициклоида» Задача по геометрии из коллекции задач Р.К. Гордина
Итак, с помощью электронных программных средств демонстрируются
а) интерактивные модели чертежей необходимых пространственных конфигураций, которые дают возможность увидеть, как изменится чертёж, если на фигуру смотреть с другой стороны;
б) готовые чертежи различных проекций пространственных тел, по которым воссоздаётся фигура, выбираются те проекции, которые могут быть для одной фигуры;
в) готовые чертежи пространственных фигур для определения взаимного расположения их частей (например, взаимного расположения прямых или плоскостей).
Приводятся примеры.
IV этап: Учащиеся должны конструировать стереометрические объекты самостоятельно на базе сформулированных ранее представлений. При этом не используется ни чертеж, ни заранее подготовленная модель, а можно лишь учителю задавать вопросы для уточнения расположения фигуры.
Схема на IV этапе: представление чертеж.
Контрольные вопросы:
1. Охарактеризуйте состав умений учащихся, овладение которыми способствует развитию пространственного мышления школьников.
2. Выделите этапы в формировании пространственных представлений школьников. Раскройте сущность каждого.
3. Рассмотрите возможности использования электронных программных средств на первом этапе. Проиллюстрируйте необходимыми примерами.
4. Рассмотрите возможности использования электронных программных средств на втором этапе. Проиллюстрируйте необходимыми примерами
5. Рассмотрите возможности использования электронных программных средств на третьем и четвёртом этапах. Проиллюстрируйте необходимыми примерами
Лекция № 2. Использование программных возможностей «Живой математики» и других электронных средств для обучения учащихся решению задач на построение в курсе планиметрии и стереометрии
Краткое содержание
В ходе лекции кратко повторяются теоретические основы обучения учащихся решению задач на построение: этапы изучения задач на построение в школе, методика работы с конкретными задачами. На втором этапе лекции рассматриваются возможности учебно-развивающей творческой среды «Живая математика» и(или) других подобных ей, например, «Математический конструктор». Особо выделяются те возможности, которые могут быть использованы для обучения учащихся решению задач на построение в курсе планиметрии и стереометрии. Демонстрируются соответствующие примеры.
Тематическое планирование материала, связанного с геометрическими построениями, предполагает следующее его распределение по этапам:
1. Ознакомительный этап (1-4 кл.). Здесь школьники впервые знакомятся с чертежными инструментами – линейкой, циркулем, треугольником и решают простейшие задачи на построение прямой, отрезка, окружности, угла.
2. Пропедевтический этап (5-6 кл.). более значительное внимание к геометрическим построениям подготавливает учащихся к решению более сложных задач систематического курса. Используются линейка, циркуль, транспортир, треугольник. Рассматривается построение параллельных и перпендикулярных прямых с помощью угольника и линейки; треугольника с помощью линейки, циркуля и транспортира; окружности, квадрата, прямоугольника.
3. Систематический курс геометрии (7-11 кл.).
7 класс. Здесь впервые учащиеся встречаются с основным требованием, предъявляемым к геометрическим чертежам – все построения должны выполняться только при помощи циркуля и линейки. Это требование вытекает из двух постулатов Евклида в «Началах»: а) от всякой точки до всякой точки можно провести прямую; б) из всякого центра любым раствором циркуля можно описать круг. При этом возникает необходимость доказательства того, что построенная фигура удовлетворяет требованиям задачи. В 7 классе учащиеся знакомятся с элементарными задачами на построение, построение окружности, вписанной и описанной около треугольника; кроме того, учащиеся усваивают первый общий метод решения задач на построение – метод геометрических мест (метод пересечений).
8 класс. В теме «Четырехугольники» решаются соответствующие задачи на построение методом геометрических мест; в теме «Движения» – используются все виды движения для решения задач на построение; в теме «Декартовы координаты на плоскости» рассматриваются построения на координатной плоскости (построение прямой, окружности, точек пересечения).
9 класс. В теме «Подобные фигуры» - задачи на построение с использованием гомотетии и преобразования подобия; в теме «Правильные многоугольники» – задачи на построение вписанных и описанных правильных многоугольников.
(10-11 классы). В стереометрии рассматриваются два вида геометрических построений: а) воображаемые построения, основывающиеся только на аксиомах стереометрии (часто используются при решении конструктивных задач типа «Докажите, что через точку вне плоскости можно провести…»; б) построения на проекционном чертеже, когда указываются кроме точек фигуры их проекции на проекционной плоскости.
Решение задач на построение выполняет свои указанные выше функции лишь при условии, когда школьники отчетливо поймут и прочно усвоят известный процесс решения этих задач, состоящий из четырех этапов, с которыми учащиеся знакомятся еще в 7 классе:
1) анализ; 2) построение (синтез); 3) доказательство; 4)исследование.
Не все указанные этапы с самого начала обязательно должны явно присутствовать при решении задач на построение. В простейших конструктивных задачах, где алгоритм построения очевиден, допустимо не проводить анализ задачи в явном виде; если же доказательство непосредственно следует из построения, его можно также опустить (например, при построении в 7-8 классах обычно либо отсутствует, либо ограничивается проверкой выполнимости каждой операции и нахождением количества решений (если возможно).
В курсе стереометрии учащиеся встречаются с двумя видами задач на построение.
1.Воображаемые построения (В.п.) – формально-логический метод построения в пространстве с отказом от реальных построений с помощью чертежных инструментов, осуществляются как бы мысленно; рисунок, их сопровождающий, носит чисто иллюстративный характер.
С математической точки зрения В.п. рассматриваются как задачи на доказательство существования фигур, определенных некоторым известными условиями. Само доказательство заключается в сведении процесса построения фигур (или их комбинаций) к конечному числу основных построений, которые определяются аксиоматически. При этом решение (доказательство) может сопровождаться, а может не сопровождаться рисунком.
Учитель обращает внимание учащихся на ряд сложностей, возникающих при осуществлении построений в пространстве (нельзя построить плоскость, многогранник и т.д.). Поэтому необходимо точно условиться: что значит выполнить то или иное построение.
Исходя из аксиом стереометрии, можно предположить возможность следующих основных построений в пространстве:
1) Плоскость может быть построена, если заданы следующие элементы, определяющие ее положение в пространстве:
а) прямая и не лежащая на ней точка,
б) две пересекающиеся прямые,
в) две параллельные прямые,
г) три точки, не лежащие на одной прямой.
2) Прямая в пространстве может быть построена как линия пересечения двух плоскостей.
3) Все планиметрические построения выполнимы в пространстве только на некоторой заданной плоскости.
4) Сфера может быть построена, если задано положение ее центра и радиуса R.
Выполнение всех остальных построений сводится к конечному числу основных.
2. На проекционном чертеже точки и прямые задаются вместе со своими проекциями на некоторую плоскость, которую называют основной.
Проекционные чертежи позволяют конструктивным средствами строить точки и линии пересечения изображаемых на нем фигур. Они имеют очень важное значение для развития пространственного воображения школьников.
С проекционными чертежами рекомендуется ознакомить школьников в 10 классе при изучении параллельной проекции ее свойств. Здесь учитель подводит школьников к выводу о том, что фигуры на чертеже могут задаваться ее проекцией на проекционной плоскости.
Основным видом стереометрических задач на построение на проекционном чертеже являются задачи на построение сечений многогранников. В школе рассматриваются два метода построения сечений:
1) метод следов; 2) метод внутреннего проектирования
(Иногда используют их комбинацию).
«Живая геометрия»
С её помощью учащиеся могут воссоздать любую геометрическую конфигурацию и изучить её математические свойства, просто перемещая объекты мышью. Все отношения геометрических объектов, заложенные при построении, сохраняются, позволяя ученикам изучить целый комплекс аналогичных случаев за несколько секунд. Значительно облегчается при этом процесс поиска контрпримеров.
Для работы не требуется специальной подготовки, но первоначальными сведениями все же учащихся необходимо вооружить. В верхней горизонтальной строчке находится меню, содержащее команды, которые позволяют выполнять построение геометрических объектов, изменять эти объекты. В левой вертикальной строке окна чертежа находится готовальня с инструментами для выполнения построений. Некоторые из них: стрелка в квадратике -- инструмент «Выделитель», необходимый для выделения объектов; точка в квадратике — инструмент «Точка», создает точки на чертеже; кисть руки в квадратике — инструмент «Текст» для создания надписей на чертежах. Чтобы выбрать из готовальни любой инструмент, необходимо щелкнуть мышью на его значке, инструмент высветится и будет активным до тех пор, пока не выбран другой.
Возможности использования рассматриваемого электронного средства.
· предъявление подвижных зрительных образов в качестве основы для осознанного овладения математическими фактами, возможность иллюстрации воображаемых построений;
· отработка в интерактивном режиме элементарных базовых умений на основе лабораторных работ в «Живой математике» по выполнению основных построений;
· усиление значимости и повышение удельного веса в учебном процессе исследовательской деятельности учащихся на заключительном этапе работы с задачей;
· увеличение объема предъявляемой для изучения информации, а также собственной практической деятельности ученика;
· увеличение доли содержательной работы ученика за счет снятия проблем технического характера, возможность вернуться к началу выполнения чертежа.
Контрольные вопросы
1. Какие этапы выделяют в изучении задач на построение в средней школе. Охарактеризуйте сущность каждого. Какова роль электронных средств на пропедевтическом этапе?
2. Какие возможности учебно-развивающей среды «Живая геометрия могут быть использованы на этапе систематического изучения задач на построение в планиметрии?
3. Что такое воображаемые построения? В чём заключается сложность выполнения таких построений для учащихся? Какие электронные средства могут помочь в преодолении указанных сложностей?
4. Как можно использовать возможности динамических геометрий при решении задач на построение сечений многогранников?
Лекция № 3. Применение инструментальных программных средств образовательного назначения для организации исследовательской деятельности школьников при изучении метода координат на плоскости и в пространстве.
Краткое содержание
На лекции рассматривается математический эксперимент как новая форма активности учащихся на уроках математики; проведение математических экспериментов с использованием ЦОР. На втором этапе лекции анализируются возможности организации исследовательской деятельности при изучении метода координат на плоскости и в пространстве.
Роль математического моделирования в обучении и, вообще, в процессе познания не нуждается в комментариях. Однако этот вид деятельности и, тем более, математический эксперимент практически отсутствовали в традиционной системе образования. Между тем, этот способ исследования всегда был присущ работе профессиональных математиков, а в наше время, благодаря компьютерам, приобрел особую важность.
Авторы большинства ЦОР уделяют таким разновидностям мультимедийных информационных источников и инструментов, как интерактивные модели и виртуальные лаборатории-конструкторы. Именно они позволяют вывести экспериментальную и исследовательскую деятельность учащихся при изучении математики на качественно новую ступень.
Высокая степень интерактивности всех моделей и возможность самостоятельно создавать сложные математические объекты и конструкции в виртуальных лабораториях ЦОР позволяет непосредственно наблюдать изменение исследуемого объекта и управлять этим изменением. Этим достигаются две цели: во-первых, внесение в учебную деятельность дополнительной привлекательности, уподобляющей ее компьютерной игре; во-вторых, возможность увидеть на фоне плавно меняющегося объекта его неизменные свойства и выявить присущие ему закономерности, – а ведь в этом и состоит, как правило, цель исследования.
Разумеется, перед авторами ЦОР стояла задача не только разработать как можно более интересные модели и лаборатории, но и снабдить их интересными практическими заданиями для изучения и освоения математических идей, понятий, методов, навыков через деятельность по созданию и исследованию математических объектов. Другими словами – в ходе математического конструирования и эксперимента. При этом тематика заданий должна, с одной стороны, обеспечить реализацию этих новых для нашего образования видов деятельности, а с другой – быть по возможности близка к содержанию стандартных курсов математики. Проанализируем, насколько успешно эти задачи решены в ЦОР [1]-[6] и рассмотрим соответствующие примеры.
Учебные наглядные пособия:
1. Электронное издание «Математика, 5-11 класс. Практикум» (ООО «Дрофа»)
2. Электронное издание «Математика, 5-11 класс» (ЗАО «1С»)
3. Открытая математика 2.5. Планиметрия (ООО «Физикон»)
4. Открытая математика 2.5. Стереометрия (ООО «Физикон»)
5. Открытая математика 2.5. Функции и графики (ООО «Физикон»)
6. Электронное издание «Математика и конструирование» (ООО «ДОС»).
[1]. Предлагаемые в этом ЦОР 12 лабораторий охватывают почти все основные линии школьного курса математики:
· числовая («Делимость чисел», «Дроби и проценты»);
· координатная («Координатная прямая», «Координатная плоскость»);
· функциональная («Графики функций», «Графики уравнений и неравенств», «Тригонометрия»);
· геометрическая («Планиметрия», «Стереометрия»);
· стохастическая («Вероятностные модели», «Анализ данных»);
· алгоритмическая («Математика и компьютер»).
Пожалуй, за рамками ЦОР осталась лишь алгебраическая линия. В то же время, количество и тематика заданий для перечисленных лабораторий явно недостаточны. В основном это задачи-исследования, которые можно найти далеко не в каждом уроке.
[3]. Экспериментальная деятельность в этом ЦОР может поддерживаться с помощью моделей и чертежа. К сожалению, в готовом виде заданий такого сорта в пособии нет. Отдельные примеры возможных экспериментов и исследований авторы вынесли в методические указания для учителя: Помощь à Методические указания à Методические материалы. Там можно найти следующие разделы:
· Компьютерное моделирование на уроках геометрии
· Применение моделей в изучении геометрии:
· Компьютерные наблюдения.
· Экспериментальные задачи-исследования.
· Расчетные задачи с последующей компьютерной проверкой
· Лабораторные работы
· Исследовательские задания.
· Компьютерный эксперимент
К сожалению, описанные в этих рекомендациях примеры компьютерных экспериментов на основе имеющихся в ЦОР моделей не совсем эффективны, т.к. при работе с моделью учащиеся одновременно видят текст с ее описанием, в котором даны ответы на те вопросы, которые нужно выяснить в эксперименте.
[4]. Как и в предыдущем ЦОР советы по проведению исследований и экспериментов можно найти лишь в методических рекомендациях: Помощь à Методические указания à Методические материалы à Наглядность в преподавании стереометрии при применении интерактивного курса.
[5]. В этом пособии дана более детальная проработка экспериментальной деятельности учащихся на основе материалов ЦОР, но тоже только на уровне отдельных примеров. Как и в [3]-[4], их можно найти в методических рекомендациях: Помощь à Методические указания à Методические материалы:
· Практическая работа «Диаграммы»
· Дидактическая игра «Прямоугольная система координат»
· Практическая работа «Координатная плоскость»
· Лабораторная работа «Преобразование графиков»
· Компьютерный эксперимент «Графическое решение систем уравнений»
· Лабораторная работа-исследование «Показательная и логарифмическая функция»
В содержание темы «Метод координат» входят следующий учебный материал: декартовы координаты на плоскости и в пространстве, формулы координат середины отрезка, расстояния между двумя точками, уравнение фигуры, уравнение прямой, уравнение плоскости.
Программа «Functor 2.9».
В заключение еще одна программа – «Functor 2.9», которую условно можно отнести к геометрическим. Она строит очень красивые многоцветные изображения поверхностей второго порядка в перспективной проекции (рис.13).
|
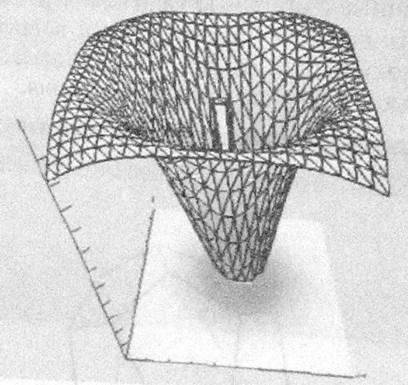Для того, чтобы получить такую поверхность, достаточно ввести в соответствующее окно функцию с двумя переменными, заданную в декартовой системе координат. Картина, которая предстанет перед глазами ученика, вряд ли оставит его равно душным. В качестве примера можно привести поверхности, заданные уравнениями: z = ln(x2 + y2); z = sin(x2 + y2) + cos(x2 + y2); z =cos(ln(x2 + y2)).
Поверхность, заданная последним уравнением, изображена на рис. 13.
Эту программу полезно использовать в начале прохождения темы «Декартовы координаты в пространстве». Ученики, вдохновленные яркими и причудливыми примерами поверхностей, легче, а главное - осознаннее воспринимают начала аналитической геометрии.
Приведенный анализ всего лишь нескольких математических программ свидетельствует о том, что многие из них учитель может с успехом использовать на уроках.
Рассмотрим примеры организации мини-исследований на уроках математике по указанной теме:
1. В ходе лабораторной работы выяснить взаимосвязь между координатами концов отрезка и его середины.
2. Исследовать и сделать вывод о зависимости взаимного расположения двух прямых на плоскости от соотношения их коэффициентов.
3. Выяснить геометрический смысл каждого коэффициента в уравнении прямой.
Контрольные вопросы:
1. Раскрыть роль математического эксперимента в обучении математике.
2. Рассмотреть возможности использования ЦОР в организации исследований на уроках математики.
3. Провести сравнительный анализ различных ЦОР на предмет организации математического эксперимента.
4. Выделить возможности организации мини-исследований по теме «Метод координат». Разработать соответствующие задания для учащихся.
Лекция № 4. Методика изучения взаимного расположения прямых и плоскостей в пространстве, возможности информационных технологий в организации зачётов по теме.
Краткое содержание
В начале лекции рассматривается краткая характеристика содержания темы «Параллельность и перпендикулярность прямых и плоскостей в пространстве», её роль в школьном курсе математики. Важность учебного материала темы для дальнейшего изучения курса стереометрии требует особого внимания к организации контроля её усвоения учащимися. Одной из форм такого контроля может быть зачёт. Далее рассматриваем особенности организации зачётов на основе использования при этом ЦОР.
Изучение параллельности и перпендикулярности прямых и плоскостей в курсе стереометрии может осуществляться в различной последовательности (сначала перпендикулярность, а затем параллельность и наоборот).
В настоящее время их изучение в школе начинается с аффинной ее части – с параллельности. Это дает возможность пораньше познакомить учащихся с изображением пространственных фигур на плоскости, позволяет показать роль аксиом при изложении этого раздела, развивать конструктивные навыки учащихся в процессе решения позиционных задач. Тема играет важную роль в процессе формирования пространственных представлений учащихся, обобщаются известные из планиметрии сведения о параллельности и перпендикулярности прямых. Основная цель изучения – дать учащимся систематические знания о параллельности и перпендикулярности прямых и плоскостей в пространстве.
II. Всю тему «параллельность в пространстве» можно разделить на 4 блока:
1) параллельность прямых в пространстве;
2) параллельность прямой и плоскости;
3) параллельность плоскостей в пространстве;
4) параллельная проекция и ее свойства. Изображение пространственных фигур на плоскости.
Для новых трех блоков можно выделить общий план изучения:
1) определение;
2) признак;
3) вопрос существования и единственности;
4) свойства (для параллельных плоскостей).
Всю тему «перпендикулярность в пространстве» можно условно разделить на три части:
1) перпендикулярность прямых в пространстве;
2) перпендикулярность прямой и плоскости;
3) перпендикулярность плоскостей.
Содержание темы:
1) перпендикулярность прямых;
2) перпендикулярность прямой и плоскости, признак перпендикулярности прямой и плоскости; перпендикуляр, наклонная, проекция наклонной на плоскость; расстояние точки до плоскости, теоремы о параллельности и перпендикулярности прямой и плоскости;
3) перпендикулярность плоскостей; теоремы о параллельности и перпендикулярности плоскостей; расстояние от прямой до параллельной ей плоскости; расстояние между параллельными плоскостями.
При изучении взаимного расположения прямых и плоскостей в пространстве широко используются стереометрический ящик, геометрия «классной комнаты», «подручные» средства (журнал, книга, ручка, мел и т.д.), аналогия с планиметрией.
1. При изучении понятий данной темы можно придерживаться следующей методической схемы:
1) формулировка определения учителем;
2) иллюстрация понятия на модели куба (параллелепипеда), геометрии «классной комнаты»;
3) логический анализ формулировки определения;
4) упражнения на распознавание понятия; приведение примеров из окружающей обстановки с соответствующим обоснованием.
3. При изучении теорем, выражающих признаки параллельности или перпендикулярности прямых и плоскостей, целесообразно придерживаться такой методической схемы:
1) мотивация изучения признака;
2) раскрытие содержания теоремы на стереометрическом ящике, на реальных объектах;
3) формулировка признака;
4) сообщение идеи доказательства, совместное составление плана доказательства;
5) оформление доказательства в соответствии с принятыми требованиями;
6) показ применимости признака на простейшей модели;
7) закрепление при решении задач.
4. Остановимся на роли задач при изучении вопросов параллельности и перпендикулярности в пространстве.
Сначала, как известно, вводится – определяется перпендикулярность (параллельность), затем рассматривается вопрос о существовании такого расположения, тесно связанный с признаками перпендикулярности (параллельности) и конструктивными задачи, т.е. воображаемыми построениями перпендикулярных (параллельных) прямых и плоскостей. Эти построения весьма разнообразны.
5.Со второй половины темы «перпендикулярность в пространстве» акцент делается уже на практические стереометрические задачи. Это обусловлено тем, что введено понятие перпендикулярности, понятие «расстояние» и рассмотрена теорема о трех перпендикулярах, дающая основную конфигурацию – классический прямоугольный треугольник (перпендикуляр, наклонная, проекция наклонной).
Одной из форм организации контроля знаний, умений и навыков является урок-зачет. В этом случае контроль не преследует цели выставить оценку, а приобретает более диагностическую направленность. На зачет, как правило, выносятся вопросы и задания, соответствующие уровню обязательной подготовки. Если учащийся справляется со всеми заданиями, то он получает "зачет", в противном случае данный материал ученик должен пересдавать. По усмотрению учителя пересдаче может подлежать как весь материал, так и только те виды заданий, с которыми ученик не справился. Зачет может быть:
- открытым (все вопросы и задания известны учащимся);
- закрытым.
Наибольшее распространение находит открытый зачет, а также комбинированная форма, когда часть вопросов известна, а некоторая часть заданий неизвестна.
В зависимости от содержания и способа взаимодействия учителя и учащихся можно выделить различные виды зачетов: текущий и тематический или итоговый зачет по теоретическим вопросам и зачет-практикум, зачет в письменной или устной форме, зачет в форме экзамена или аукциона, дифференцированный зачет и т. д.
Рассмотрим возможные основные этапы подготовки и проведения различных уроков-зачетов.