Лабораторная Работа
На тему: НАХОЖДЕНИЕ КОРНЯ НЕЛИНЕЙНОГО УРАВНЕНИЯ. МЕТОДЫРЕШЕНИЯ СИСТЕМЫНЕЛИНЕЙНЫХ УРАВНЕНИЙ
Москва, 2008 год
НАХОЖДЕНИЕ КОРНЯ НЕЛИНЕЙНОГО УРАВНЕНИЯ
Постановка задачи
Пусть задана функция  , непрерывная вместе со своими несколькими производными. Требуется найти все или некоторые вещественные корни уравнения
, непрерывная вместе со своими несколькими производными. Требуется найти все или некоторые вещественные корни уравнения
 . (1)
. (1)
Данная задача распадается на несколько подзадач. Во-первых, необходимо определить количество корней, исследовать их характер и расположение. Во-вторых, найти приближенные значения корней. В-третьих, выбрать из них интересующие нас корни и вычислить их с требуемой точностью e. Первая и вторая задачи решаются, как правило, аналитическими или графическими методами. В случае, когда ищутся только вещественные корни уравнения (1), полезно составить таблицу значений функции  . Если в двух соседних узлах таблицы функция имеет разные знаки, то между этими узлами лежит нечетное число корней уравнения (по меньшей мере, один). Если эти узлы близки, то, скорее всего, корень между ними только один.
. Если в двух соседних узлах таблицы функция имеет разные знаки, то между этими узлами лежит нечетное число корней уравнения (по меньшей мере, один). Если эти узлы близки, то, скорее всего, корень между ними только один.
Найденные приближенные значения корней можно уточнить с помощью различных итерационных методов. Рассмотрим три метода: 1) метод дихотомиии (или деление отрезка пополам); 2) метод простой итерации и 3) метод Ньютона.
Методы решения задачи
Метод деления отpезка пополам
Наиболее простым методом, позволяющим найти корень нелинейного уравнения (1), является метод половинного деления.
Пусть на отрезке [a, b] задана непрерывная функция  Если значения функции на концах отрезка имеют разные знаки, т.е.
Если значения функции на концах отрезка имеют разные знаки, т.е.  то это означает, что внутри данного отрезка находится нечетное число корней. Пусть для определенности корень один. Суть метода состоит в сокращении на каждой итерации вдвое длины отрезка. Находим середину отрезка [a,b] (см. рис. 1)
то это означает, что внутри данного отрезка находится нечетное число корней. Пусть для определенности корень один. Суть метода состоит в сокращении на каждой итерации вдвое длины отрезка. Находим середину отрезка [a,b] (см. рис. 1)  Вычисляем значение функции
Вычисляем значение функции  и выбираем тот отрезок, на котором функция
и выбираем тот отрезок, на котором функция  меняет свой знак. Новый отрезок вновь делим пополам. И этот процесс продолжаем до тех пор, пока длина отрезка не сравняется с наперед заданной погрешностью вычисления корня e. Построение нескольких последовательных приближений по формуле (3) приведено на рисунке 1.
меняет свой знак. Новый отрезок вновь делим пополам. И этот процесс продолжаем до тех пор, пока длина отрезка не сравняется с наперед заданной погрешностью вычисления корня e. Построение нескольких последовательных приближений по формуле (3) приведено на рисунке 1.
Итак, алгоритм метода дихотомии:
1. Задать отрезок [a,b] и погрешность e.
2. Если f(a) и f(b) имеют одинаковые знаки, выдать сообщение о невозможности отыскания корня и остановиться.

Рис.1. Метод деления отрезка пополам для решения уравнения вида f(х)=0.
3. В противном случае вычислить c=(a+b)/2
4. Если f(a) и f(c) имеют разные знаки, положить b=c, в противном случае a=c.
5. Если длина нового отрезка  , то вычислить значение корня c=(a+b)/2 и остановиться, в противном случае перейти к шагу 3.
, то вычислить значение корня c=(a+b)/2 и остановиться, в противном случае перейти к шагу 3.
Так как за N шагов длина отрезка [a, b] сокращается в 2N раз, то заданная погрешность отыскания корня e будет достигнута за итераций.

Как видно, скорость сходимости мала, но к достоинствам метода относятся простота и безусловная сходимость итерационного процесса. Если отрезок [a, b] содержит больше одного корня (но нечетное число), то всегда будет найден какой-нибудь один.
Замечание. Для определения интервала, в котором лежит корень, необходим дополнительный анализ функции  , основанный либо на аналитических оценках, либо на использование графического способа решения. Можно также организовать перебор значений функции в различных точках, пока не встретится условие знакопеременности функции
, основанный либо на аналитических оценках, либо на использование графического способа решения. Можно также организовать перебор значений функции в различных точках, пока не встретится условие знакопеременности функции 
Метод простой итерации
При использовании этого метода исходное нелинейное уравнение (1) необходимо переписать в виде
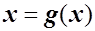 (2)
(2)
Обозначим корень этого уравнения C*. Пусть известно начальное приближение корня  . Подставляя это значение в правую часть уравнения (2), получаем новое приближение
. Подставляя это значение в правую часть уравнения (2), получаем новое приближение

и т.д. Для (n+1)- шага получим следующее приближение
 (3)
(3)
Таким образом, по формуле (3) получаем последовательность С0, С1,…,Сn+1, которая стремиться к корню С* при n®¥. Итерационный процесс прекращается, если результаты двух последовательных итераций близки, т. е. выполняется условие
 (4)
(4)
Исследуем условие и скорость сходимости числовой последовательности {C n} при n®¥. Напомним определение скорости сходимости. Последовательность {Cn}, сходящаяся к пределу С*, имеет скорость сходимости порядка a, если при n®¥ выполняется условие
 (5)
(5)
Допустим, что  имеет непрерывную производную, тогда погрешность на (n+1)-м итерационном шаге en+1=Cn+1-C*=g(Cn)-g(C*) можно представить в виде ряда
имеет непрерывную производную, тогда погрешность на (n+1)-м итерационном шаге en+1=Cn+1-C*=g(Cn)-g(C*) можно представить в виде ряда
en+1 » Cn+1 – C* = g¢(C*) (Cn-C*) +¼@ g¢(C*) en+¼
Таким образом, получаем, что при выполнении условия
çg¢(C*) ç< 1 (6)
последовательность (3) будет сходиться к корню с линейной скоростью a=1. Условие (6) является условием сходимости метода простой итерации. Очевидно, что успех метода зависит от того, насколько удачно выбрана функция  .
.
Например, для извлечения квадратного корня, т. е. решения уравнения вида x =a2, можно положить
x=g1(x)=a/x (7а)
или
x=g2(x)=(x+a/x)/2. (7б)
Нетрудно показать, что
½g1'(C)½=1,
½g2'(C)½<1.
Таким образом, первый процесс (7а) вообще не сходится, а второй (7б) сходится при любом начальном приближении С0 >0.
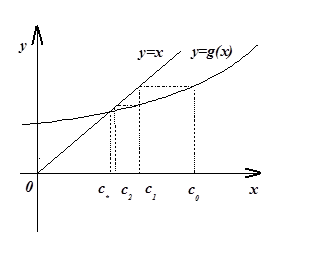
Рис. 2. Графическая интерпретация метода простых итераций для решения уравнения вида x=g(х).
Построение нескольких последовательных приближений по формуле (3)
С0, С1, …, Сn = C*
приведено на рисунке 2.
Метод Ньютона
В литературе этот метод часто называют методом касательных, а также методом линеаризации. Выбираем начальное приближение С0. Допустим, что отклонение С0 от истинного значения корня С* мало, тогда, разлагая f(C*) в ряд Тейлора в точке С0, получим
f(C*) = f(C0) + f ¢(C0) (C*-C0) +¼ (8)
Если f ¢(C0) ¹ 0, то в (8) можно ограничится линейными по DC =C-C0 членами. Учитывая, что f(C*)=0, из (9) можно найти следующее приближение для корня
C1 = C0 – f (C0) / f¢(C0)
или для (n+1)-го приближения
Cn+1= C n – f (C n) / f ¢(C n) (9)
Для окончания итерационного процесса можно использовать одно из двух условий
çCn+1 – Cn ç< e
или
çf(Cn+1) ç< e.
Исследование сходимости метода Ньютона проводится аналогично предыдущему случаю. Самостоятельно получить, что при выполнении условия
½f ''(C)/2f'(C)½<1. 

метод Ньютона имеет квадратичную скорость сходимости ( ).
).

Рис. 3. Графическая интерпретация метода Ньютона для решения уравнения вида f(х)=0.
Построение нескольких последовательных приближений по формуле (9)
С0, С1, …, Сn = C*
приведено на рисунке 3.
Задание
1. Для заданной функции f(x)
· определите число вещественных корней уравнения f(x)=0, место их расположения и приближенные значения (постройте график или распечатайте таблицу значений).
· Вычислите один из найденных корней (любой) с точностью e=0,5*10-3.
Для вычислений используйте метод деления отрезка пополам (определите число итераций), а затем этот же корень найдите с помощью метода Ньютона (также определив число итерационных шагов).
Сравните полученные результаты.
Варианты заданий
1. x3 –3x2 +6x – 5 = 0 2. x 3 +sin x –12x-1=0
3. x3 –3x2 –14x – 8 = 0 4. 3x + cos x + 1 =0
5. x2 +4sin x –1 = 0 6. 4x –ln x = 5
7. x6 –3x2 +x – 1 = 0 8. x3 – 0.1x2 +0.3x –0.6 = 0
9.  10. (x -1)3 + 0.5ex = 0
10. (x -1)3 + 0.5ex = 0
11.  12. x5 –3x2 + 1 = 0
12. x5 –3x2 + 1 = 0
13. x3 –4x2 –10x –10 = 0 14. 
15.  16.
16. 
17.  18.
18. 
19. 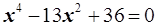 20.
20. 
21.  22.
22. 
23.  24. x 4- 2.9x3 +0.1x2 + 5.8x - 4.2=0
24. x 4- 2.9x3 +0.1x2 + 5.8x - 4.2=0
25. x4+2.83x3- 4.5x2-64x-20=0 26. 