0 1 2 3 …
 |
Определение. Натуральным числом называют отличное от нуля целое неотрицательное число.
Множество натуральных чисел обозначают символом N, целых неотрицательных чисел символом N0, то есть N0={0}  N.
N.
Каждый класс разбиения характерен тем, что содержит равночисленные множества и определяется любым своим представителем. Следовательно, любое целое неотрицательное число а можно рассматривать как характеристику мощности каждого множества, находящегося в классе а.
Определение.Целое неотрицательное число а называют количеством элементов множества А, если множество А является представителем числа а, то есть n(A)=а 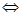 А
А  а.
а.
Итак, неотрицательное число 2 — это имя класса равномощных друг другу конечных множеств.
Следовательно, имя — символ «2 » — это количественное целое неотрицательное число; значением числа 2 является класс, в котором находятся все множества, равномощные, например, множеству В = {а, в}. Т.к. множество В принадлежит классу равномощных множеств, обозначенному символом 2 (А  2), то оно является представителем этого класса, т. е. {а, в} = А2. Значением числа m является тот класс равномощных конечных множеств, собственным именем которого оно является.
2), то оно является представителем этого класса, т. е. {а, в} = А2. Значением числа m является тот класс равномощных конечных множеств, собственным именем которого оно является.
Смысл числа m заключается в том, что число характеризует класс элементов любого конечного множества, принадлежащего классу, именем которого является.
Определение.Натуральным числовым рядом называют упорядоченное отношением «меньше» множество всех натуральных чисел.
Определение.Отрезком Nа натурального числового ряда называют упорядоченное отношением «меньше» множество натуральных чисел, каждое из которых меньше числа а или равно ему.
Определение.Установление взаимнооднозначного соответствия между элементами непустого конечного множества А и отрезком натурального числового ряда, называют счетом элементов множества А.
Результат счета не зависит от порядка счета. Например: проведем счет элементов множества X = {а, в, с, d}.
Пусть f = {(а, 1); (в, 2); (с, 3); (d, 4)}. Т.к. f — биекция множества X на N4, то по определению f — это счет элементов множества X.
I признак равенства. Число m равно числу p, тогда и только тогда, когда существует представитель числа m, равномощный некоторому представителю числа p: m = p 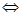 (
(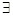 Am, Ap)[Am~Ap]
Am, Ap)[Am~Ap]
Доказательство. Пусть m, p — произвольные целые неотрицательные числа Аm, Аp — некоторые их представители. Докажем, что если m = p  Am ~ Ap.
Am ~ Ap.
Если m = p, то они определяют один и тот же класс разбиения М / ~. Следовательно Аm и Аp находятся в одном классе равномощных множеств и следовательно Am ~ Ap.
Докажем, что если Am ~ Ap  m = p. Если Am ~ Ap, то всякий элемент класса m — это множество равномощное Аm следовательно равномощное и Аp и поэтому находится в одном с ним классе, а именно в классе p. Так как любой элемент класса m является элементом класса p, то класс m есть подмножество класса p. Аналогично доказывается, что класс p есть подмножество класса m. Значит класс m равен классу p, т.е. числа m и p определяют один и тот же класс разбиения М / ~, т.е. m = p.
m = p. Если Am ~ Ap, то всякий элемент класса m — это множество равномощное Аm следовательно равномощное и Аp и поэтому находится в одном с ним классе, а именно в классе p. Так как любой элемент класса m является элементом класса p, то класс m есть подмножество класса p. Аналогично доказывается, что класс p есть подмножество класса m. Значит класс m равен классу p, т.е. числа m и p определяют один и тот же класс разбиения М / ~, т.е. m = p.
II признак равенства. Число m равно числу p тогда и только, тогда представители чисел m и p, являющиеся представителями цепочки  , равны. m = p
, равны. m = p 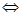 Qm = Qp
Qm = Qp
Теорема. Отношение «равно» является эквивалентностью, т.е. обладает свойствами рефлексивности, симметричности, транзитивности).
1. Рефлексивность отношения «равно», то есть ( х
х  N0)[х = х].
N0)[х = х].
2. Симметричность отношения «равно». ( х, у
х, у  N0)[х = у
N0)[х = у  у = х].
у = х].
3. Транзитивность отношения «равно». ( х, у, z
х, у, z  N0)[x = y
N0)[x = y  y = z
y = z  x = z].
x = z].
Доказательство. Пусть m, p — произвольные целое неотрицательное число. По условию х=у  у=z
у=z  Qх=Qу
Qх=Qу  Qу=Qz
Qу=Qz  Qх = Qz
Qх = Qz  х = z.
х = z.
Определение 1.Целое неотрицательное число m меньше целое неотрицательное число p (или число p больше числа m), если существует представитель числа m, являющийся подмножеством некоторого представителя числа p и неравного ему, то есть m < p 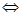 (
(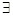 Am, Ap)[Am
Am, Ap)[Am 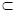 Ap
Ap  Am
Am 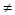 Ap]
Ap]
Определение 2.Целое неотрицательное число m меньше целого неотрицательного числа p (или p больше числа m), если Qm подмножество Qp и неравно ему, то есть m < p 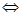 Qm
Qm 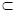 Qp
Qp  Qm
Qm 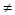 Qp.
Qp.
Из определения очевидно, что m < p 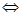 p > m.
p > m.
Теорема. Отношение «меньше» на множестве N0 является отношением строго линейного порядка. Следовательно, отношение «меньше» является антирефлексивным, антисимметричным и транзитивным, линейным.
Доказательство. Докажем антирефлексивность отношения «меньше», то есть ( х
х  N0)[
N0)[  ] методом от противного. Пусть (
] методом от противного. Пусть (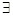 х
х  N0)[х < х]. Если х < х
N0)[х < х]. Если х < х  (по лемме) х
(по лемме) х 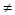 х, что противоречит рефлексивности равенства чисел
х, что противоречит рефлексивности равенства чисел  (
(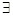 х
х  N0)[х < х]
N0)[х < х]  Л
Л  (
( х
х  N0)[
N0)[  ].
].
Антисимметричность отношения «меньше», то есть ( х, у
х, у  N0)[х < у
N0)[х < у 
 ].
].
Доказательство. Докажем антисимметричность отношения «меньше» методом от противного. Пусть х<у и у<х  (Qх
(Qх 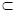 Qу
Qу  Qх
Qх 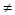 Qу)
Qу)  (Qу
(Qу 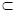 Qх
Qх  Qу
Qу 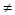 Qх)
Qх)  (Qх
(Qх 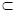 Qу
Qу  Qу
Qу 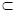 Qх)
Qх)  (Qх
(Qх 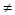 Qу) что противоречит определению отношения «равно»
Qу) что противоречит определению отношения «равно»  Qх = Qу
Qх = Qу  Qх
Qх 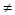 Qу, чего быть не может следовательно (
Qу, чего быть не может следовательно ( х, у
х, у  N0)[х < у
N0)[х < у 
 ].
].
Транзитивность отношения «меньше»,то есть ( х, у, z
х, у, z  N0)[х < у
N0)[х < у  у < z
у < z  x < z].
x < z].
Доказательство. Докажем транзитивность отношения «меньше». Пусть x, y, z — целое неотрицательное число Qх, Qу , Qz — их представители. По условию х < у и у < z следовательно по определению отношения «меньше» (Qх 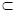 Qу
Qу  Qх
Qх 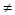 Qу)
Qу)  (Qу
(Qу 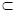 Qz
Qz  Qу
Qу 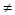 Qz) следовательно по определению подмножества Qх
Qz) следовательно по определению подмножества Qх 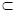 Qz
Qz  Qх
Qх 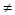 Qz следовательно по определению отношения «меньше» х < z.
Qz следовательно по определению отношения «меньше» х < z.
Линейность отношения «меньше», то есть ( х, у
х, у  N0)[х
N0)[х 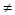 у
у  х < у
х < у 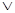 у < х].
у < х].