Согласно изложенному, основным содержанием метода тенденций является экстраполирование хронологического графика уровня или расхода на несколько дней вперед.
Вместе с этим известно, что экстраполирование любой кривой (в том числе и кривой колебания уровня) может быть произведена несколькими способами, которые отличаются друг от друга исходными предпосылками и точностью. Таким образом, точность прогнозов по методу тенденций зависит прежде всего от способа экстраполирования графика изменения стока.
Все существующие способы экстраполирования можно разбить на две группы: а) линейные и б) нелинейные.
Способ линейного экстраполирования основан на предположении постоянства градиента рассматриваемого элемента во времени, т.е.
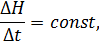
где H – уровень или расход воды.
Исходя из этой предпосылки, экстраполирование уровня или расхода воды производится по прямой линии, наклон которой к осям координат равен среднему наклону последнего (перед днем выпуска прогноза) отрезка гидрографа.
В отличие от этого способа нелинейное экстраполирование основано на предположении о непостоянстве градиента изменения уровня или расхода во времени, т.е.

Экстраполирование гидрографа стока производится в этом случае по кривой, уравнение которой устанавливается аналитическим или графическим путем.
В соответствии с указанным подразделением прогнозы стока по методу тенденций могут быть подразделены на прогнозы по линейной тенденции и прогнозы по нелинейной тенденции.
Изложение этих способов приводится ниже.
3. ПРОГНОЗЫПО ЛИНЕЙНОЙ ТЕНДЕНЦИИ [1, 6, 11]
Практическое осуществление этого способа производится следующим образом.
Предположим, имеется отрезок гидрографа уровня (рис.3) за период от  до
до  , причем
, причем  – сегодняшний день или день выпуска прогноза.
– сегодняшний день или день выпуска прогноза.
 Рис. 3. Схема линейного изменения уровня во времени.
Рис. 3. Схема линейного изменения уровня во времени.
| Предположим, требуется дать прогноз уровня в момент 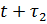 (т.е. с заблаговременностью (т.е. с заблаговременностью 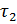 ).
Обозначим приращение уровня в период от ).
Обозначим приращение уровня в период от  до до 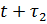 через через  , а приращение уровня в прошлый период от , а приращение уровня в прошлый период от  до до 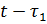 через через  . Тогда . Тогда
|
где  – уровень в момент
– уровень в момент 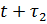 , т.е. прогноз уровня с заблаговременностью
, т.е. прогноз уровня с заблаговременностью 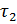 ;
;
 - уровень в момент
- уровень в момент  (сегодняшний день);
(сегодняшний день);
 – уровень в момент
– уровень в момент 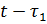 (уровень в прошлый момент времени);
(уровень в прошлый момент времени);
 – суммарное изменение уровня от момента
– суммарное изменение уровня от момента 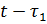 до момента
до момента 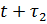 .
.
Так как, согласно исходной предпосылке способа,  то, принимая
то, принимая  и
и  , получим
, получим

| (5.2) |
и, следовательно

| (6.2) |
Их равенств (5.2) и (6.2) следует, что величины  и
и 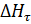 в уравнениях (3.2) и (4.2) могут быть определены по связям
в уравнениях (3.2) и (4.2) могут быть определены по связям
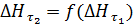
| (7.2) |
и
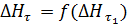
| (8.2) |
т.е. по градиентам изменения уровня за прошлый период времени.
Наиболее распространен на практике прогноз уровня и расхода по уравнению (4.2). при использовании этого уравнения для прогноза стока производится построение графической зависимости (8.2) по материалам гидрометрическим наблюдений в данном створе за прошлый период времени.
Обработка указанных материалов производится по форме табл. 3. В гр. 1 и 2 таблицы вписываются даты и уровень (или расход) воды в данном створе реки, в гр. 3 и 4 – разности уровней за периоды  и
и 
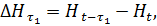
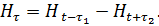
Величины  и
и 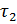 устанавливаются заранее, исходя из требующейся заблаговременности и допустимой точности прогнозов (в табл. 3 принято
устанавливаются заранее, исходя из требующейся заблаговременности и допустимой точности прогнозов (в табл. 3 принято  ).
).
Графическая зависимость (8.2) строится по данным гр. 3 и 4, табл. 1 (рис.4), причем по вертикальной шкале откладываются величины  , а по горизонтальной -
, а по горизонтальной - 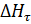 . Связь на этом графике проводится в виде средней линии в поле точек. Отклонения точек от этой линии (по горизонтальной оси) равны ошибкам прогноза по уравнению (4.2); поэтому обеспеченность способа может быть определена как отношение числа точек, отклонение которых от средней линии не превышает допустимой величины (20% от
. Связь на этом графике проводится в виде средней линии в поле точек. Отклонения точек от этой линии (по горизонтальной оси) равны ошибкам прогноза по уравнению (4.2); поэтому обеспеченность способа может быть определена как отношение числа точек, отклонение которых от средней линии не превышает допустимой величины (20% от 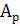 ), к общему числу точек на поле графика.
), к общему числу точек на поле графика.
Зависимости вида (8.2) строятся обычно для каждого сезона в отдельности: для весеннего половодья, летней и зимней межени.
Каждая из этих связей строится по 30-50 точкам, равномерно охватывающим всю амплитуду колебания уровня (расхода) в данном сезоне за многолетний период времени (обычно за 5-6 последних лет).
Прогноз стока по зависимостям вида (8.2) весьма прост: по данным о величинах изменения уровня на прошлый интервал времени  с рис. 4 снимается прогнозное изменение уровня за период
с рис. 4 снимается прогнозное изменение уровня за период  и дается прогноз уровня по уравнению (4.2).
и дается прогноз уровня по уравнению (4.2).

Рис. 4. Связь для прогноза уровня по линейной тенденции (р. Волга – г. Елабуга).
 ,
или
,
или
 ,
,