Способы нелинейной тенденции применяются обычно для прогнозов большой заблаговременности (в среднем свыше 4-5 дней), когда предположение о постоянстве градиента уровня или расхода оказывается явно несправедливым.
Основным содержанием этих способов является экстраполирование гидрографа стока по кривой 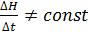 . В общем случае подобное экстраполирование производится по уравнению предшествующего (перед днем выпуска прогноза) отрезка гидрографа; таким образом, основной предпосылкой способов нелинейной тенденции является предположение о постоянстве закона изменения стока в рассматриваемый период времени.
. В общем случае подобное экстраполирование производится по уравнению предшествующего (перед днем выпуска прогноза) отрезка гидрографа; таким образом, основной предпосылкой способов нелинейной тенденции является предположение о постоянстве закона изменения стока в рассматриваемый период времени.
В этой предпосылке и преимущество и недостаток рассматриваемых способов. Преимущество заключается в том, что нелинейность гидрографа соответствует естественным условиям формирования стока на речных бассейнах. Подъемы и спады уровня на реках характеризуются, как правило, переменной интенсивностью, и гидрограф уровня в виде прямой линии встречается как редкое исключение. Поэтому предположение и непостоянстве градиентов стока в период заблаговременности прогноза соответствует физике явления и, следовательно, имеет определенной преимущество по сравнению с приближенной предпосылкой рассмотренного выше способа линейной тенденции.
 Рис. 5. Схема влияния осадков на характер изменения уровня или расхода.
Рис. 5. Схема влияния осадков на характер изменения уровня или расхода.
| Недостатком способов нелинейной тенденции является ограниченность их применения: они могут быть использованы только для прогноза продолжительных и интенсивных периодов спада. Это иллюстрируется графиком на рис.5, на котором представлен отрезок гидрографа в период незначительного подъема, переходящего в спад, и показаны возможные варианты экстраполирования этого отрезка на период  от даты выпуска прогноза t. Казалось бы, что наилучшим из этих вариантов является вариант нелинейного от даты выпуска прогноза t. Казалось бы, что наилучшим из этих вариантов является вариант нелинейного
|
экстраполирования по линии ab, так как в этом случае учитывается закономерность изменения стока в период  . Однако подобное заключение справедливо лишь при отсутствии осадков в период
. Однако подобное заключение справедливо лишь при отсутствии осадков в период  . Если же в этот период (от момента t) выпадут осадки, то фактическое изменение стока будет происходить не по ab, а по линии ac, так как в этом случае увеличивается боковой приток в русловую сеть. Поэтому прогноз по нелинейной тенденции ab при выпадении осадков является неудовлетворительным, так как ошибка прогноза примерно в 2 раза превысит в этом случае ошибку прогноза по линейной тенденции aa’.
. Если же в этот период (от момента t) выпадут осадки, то фактическое изменение стока будет происходить не по ab, а по линии ac, так как в этом случае увеличивается боковой приток в русловую сеть. Поэтому прогноз по нелинейной тенденции ab при выпадении осадков является неудовлетворительным, так как ошибка прогноза примерно в 2 раза превысит в этом случае ошибку прогноза по линейной тенденции aa’.
Из этого следует, что нелинейное экстраполирование может быть использовано для прогнозов стока только в бездождные периоды, т.е. в периоды минимального бокового притока в русловую сеть. А так как бездождные периоды характеризуются, как правило, спадом уровня (исключая случаи искусственного регулирования), то, следовательно, способы нелинейной тенденции применимы лишь для прогнозов спада.
В отличие от этого способ линейной тенденции применим (при небольшой заблаговременности) как в периоды спада, так и в периоды подъема; прогноз по этому способу дается по прямой aa’ (рис. 5) и, следовательно, ошибка прогноза от фазы изменения стока не зависит.
Согласно изложенному, нелинейное экстраполирование производится путем подбора уравнения, определяющего закон изменения стока в период спада. Поэтому перед изложением способов подбора этого уравнения рассмотрим факторы, определяющие режим стока в периоды спада.
Известно, что колебания стока на естественных водосборах определяются в основном колебаниями притока в русловую сеть (т.е. колебаниями стока поверхностных и грунтовых вод), а также явлениями аккумуляции и интерференции паводков в русловой сети. В свою очередь колебания притока в период спада определяются суммарным запасом воды в бассейне в начале спада и физико-географическими характеристиками водосбора, главным образом рельефом, характером почв, глубиной залегания и уклонами водоносных пластов, лесистостью и озерностью.
Таким образом, можно написать

где  – расход воды в замыкающем створе в момент t (считая от начала спада),
– расход воды в замыкающем створе в момент t (считая от начала спада),
 – суммарный запас воды на площади бассейна в начале спада,
– суммарный запас воды на площади бассейна в начале спада,
 – индекс физико-географических характеристик бассейна.
– индекс физико-географических характеристик бассейна.
Принимая в этом равенстве (для каждого бассейна в отдельности)  , получим для начала спада
, получим для начала спада

| (10.2) |
и, следовательно

| (11.2) |
где  – расход воды в замыкающем створе в начале спада.
– расход воды в замыкающем створе в начале спада.
Равенство (11.2) является исходной зависимостью способов нелинейной тенденции, и, следовательно, разработка прогнозов этими способами заключается в установлении связи между расходом воды в момент времени t (от начала спада) и максимальным расходом на гребне паводочной волны. Построение подобных связей производится в настоящее время аналитическим и графическим способами. Описание этих способов изложено ниже.
Аналитический способ прогноза.
Аналитический способ прогноза по нелинейной тенденции основан на предположении, что процесс спада в руслах естественных водотоков выражается уравнением экспотенциальной кривой.

где  – время от начала спада,
– время от начала спада,
 и
и  – коэффициенты экспотенциальной кривой,
– коэффициенты экспотенциальной кривой,
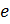 – основание натуральных логарифмов.
– основание натуральных логарифмов.
Согласно многочисленным исследованиям [1, 2, 5, 7, 8, 9, 11], уравнение (12.2) в большинстве случаев достаточно хорошо выражает процесс истощения запасов руслового стока и поэтому может быть использовано для прогнозов в период спада.
Наилучшие результаты получаются при использовании этого уравнения на реках с однородным грунтовым питанием в период спада; если же часть спада сформирована поверхностным током, а часть – грунтовым стоком, то точность расчетов понижается, что объясняется различием в процессах стока поверхностных и грунтовых вод на площади бассейна.
Разработка прогнозов по уравнению (12.2) заключается в подборе коэффициентов  и
и  для данного замыкающего створа по материалам многолетних гидрометрических наблюдений. Подбор этих коэффициентов производится следующим образом.
для данного замыкающего створа по материалам многолетних гидрометрических наблюдений. Подбор этих коэффициентов производится следующим образом.
Произведем двойное логарифмированное уравнение (12.2). логарифмируя первый раз, получим

откуда

Логарифмируя это равенство вторично, получим

| (13.2) |
где 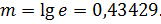
Уравнение (13.2) является линейным; таким образом, коэффициенты  и
и  могут быть определены путем графического решения этого уравнения.
могут быть определены путем графического решения этого уравнения.
С этой целью из материалов гидрометрических наблюдений за прошлые годы выбирается несколько устойчивых продолжительных и генетически однородных спадов (например, несколько спадов весеннего половодья) и для каждого из них строится логарифмическая анаморфоза по уравнению (13.2). Затем в поле логарифмических анаморфоз проводится средняя прямая линия (рис. 6), по которой и определяются искомые коэффициенты  и
и  ; кэффициент
; кэффициент  определяется как тангенс угла наклона средней линии к оси
определяется как тангенс угла наклона средней линии к оси 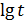 , а коэффициент
, а коэффициент  находится из отрезка
находится из отрезка  , который отсекается прямой на вертикальной оси координат.
, который отсекается прямой на вертикальной оси координат.
Исследование применимости (12.2) для прогнозов спада половодья было выполнено Б.А. Аполловым, М. Шокличем и другими исследователями. Так, например, Б.А. Аполловым и М. Кунщиковой [1] получено для прогноза спада половодья на р. Москва – г. Звенигород уравнение

Аналогичное уравнение было получено Шокличем для периодов спада на р. Рейн – Листенау [1]

Успешно было использовано уравнение (12.2) и для прогноза уровней в период спада на р. Сухона [10].
Из приведенных примеров следует, что коэффициент  в уравнении (12.2) в большинстве случаев равен единице и, следовательно, с практически достаточной точностью прогнозов спада может быть использовано уравнение в уравнении (12.2) в большинстве случаев равен единице и, следовательно, с практически достаточной точностью прогнозов спада может быть использовано уравнение
|  Рис. 6. Логарифмические анаморфозы спада уровня.
Рис. 6. Логарифмические анаморфозы спада уровня.
|
реках примерно от 0,01 до 0,2. Согласно К.П. Воскресенскому [2], коэффициент  зависит от скорости стекания воды с площади бассейна и, следовательно, определяется физико-географическими особенностями водосборов и видом питания реки на спаде. Последнее объясняется тем, что скорость стекания поверхностных вод отличается от скорости стекания грунтовых вод и, следовательно, величина коэффициента
зависит от скорости стекания воды с площади бассейна и, следовательно, определяется физико-географическими особенностями водосборов и видом питания реки на спаде. Последнее объясняется тем, что скорость стекания поверхностных вод отличается от скорости стекания грунтовых вод и, следовательно, величина коэффициента  зависит от вида преобладающего питания реки. По этой причине коэффициент
зависит от вида преобладающего питания реки. По этой причине коэффициент  не только применен для различных бассейнов, но и не остается постоянным в многолетнем разрезе для данного бассейна, так как условия питания реки не остаются постоянными во времени.
не только применен для различных бассейнов, но и не остается постоянным в многолетнем разрезе для данного бассейна, так как условия питания реки не остаются постоянными во времени.

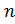 коэффициент
коэффициент  не остается постоянным для всех водосборов и колеблется на различных
не остается постоянным для всех водосборов и колеблется на различных