Технические характеристики СИ, оказывающие влияние на результаты и погрешности измерений, называются метрологическими характеристиками(МХ)
От точности характеристик при изготовлении СИ, стабильности их в процессе эксплуатации зависит точность результатов измерений.
К метрологическим характеристикам относятся: функции преобразования ИП, чувствительность измерительного прибора, цена деления шкалы аналогового ИП, порог чувствительности, диапазон измерений, вариация показаний, надежность СИ и т.д.
Функция преобразования ИП (градуировочная характеристика, уравнение преобразования) - это зависимость между выходным сигналом измерительного прибора  и его входным сигналом
и его входным сигналом 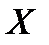
 (1)
(1)
в неявной форме, а для прибора прямого действия (рис.1) можно записать
 (2)
(2)
где  =
= 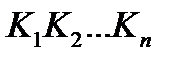 - коэффициент прямого преобразования.
- коэффициент прямого преобразования.
Эта функция может быть представлена аналитически, графически или в виде таблицы. Идеальная функция преобразования представляет линейную зависимость (рис.3), но под действием каких либо причин может иметь нелинейный вид (рис.4).
У
dy 

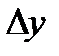
dx
0 
 Х Рис.3
Х Рис.3 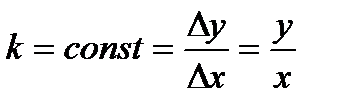 ;
;
const - коэф. преобр. для идеальных ИП.
У
dy
y=k(x)x

dx

0  x
x
Рис.4 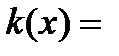 vari
vari  vari- для реальных.
vari- для реальных.
Для прибора уравновешивающего преобразования функция преобразования записывается в виде
 (3)
(3)
где 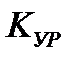 - коэффициент преобразования измерительного прибора сравнения.
- коэффициент преобразования измерительного прибора сравнения.
Если функция преобразования прибора в целом линейна, то в соответствии с рис.2 можно записать

 СУ
СУ 


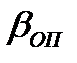
 (4)
(4)
- результат сравнения, действующий на входе цепи прямого преобразования;
 (5)
(5)
- коэффициент преобразования цепи обратного преобразования;
 (6)
(6)
- коэффициент преобразования цепи прямого преобразования.
Тогда коэффициент уравновешивающего преобразования с учетом (4), (5) и (6)
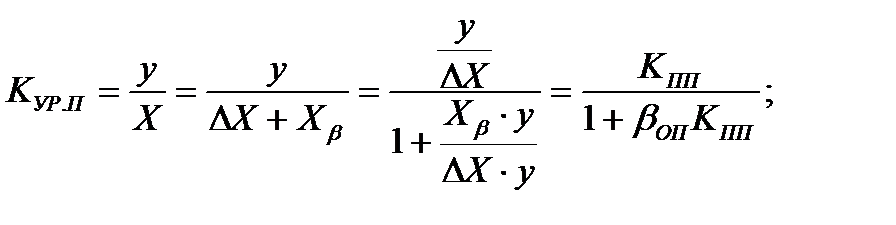 (7)
(7)
Таким образом, общий коэффициент уравновешивающего преобразования  в
в  раз меньше коэффициента прямого преобразования.
раз меньше коэффициента прямого преобразования.
Если  , то
, то  , т.е. качество цепи прямого преобразования практически не влияет на качество работы прибора в целом.
, т.е. качество цепи прямого преобразования практически не влияет на качество работы прибора в целом.
Вывод: воздействие дестабилизирующих факторов на  не влияет на характеристику СИ при большем
не влияет на характеристику СИ при большем  .
.
Чувствительность измерительного прибора - характеризует способность прибора реагировать на изменения входного сигнала.
Чувствительность определяется из уравнения преобразования и представляет собой отношение изменения сигнала 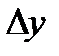 на выходе прибора к вызывающему его изменению сигнала
на выходе прибора к вызывающему его изменению сигнала  на входе прибора:
на входе прибора:
 - общий вид (8)
- общий вид (8)
При линейном уравнении преобразования
 (9)
(9)
При нелинейном уравнении чувствительность зависит от уровня входного сигнала и может быть найдена в заданной области характеристики преобразования
 = vari (10)
= vari (10)
Сопоставляя (9) с (2) и (3) нетрудно заметить, что чувствительность S совпадает с коэффициентом преобразования K.
Цена деления шкалы аналогового ИП (или постоянная прибора) - разность значений величин, соответствующих двум соседним отметкам шкалы. Она связана с чувствительностью зависимостью
 (11)
(11)
Чувствительность и цена деления - величины размерные. Например, для аналогового стрелочного вольтметра если  , то
, то  .
.

Порог чувствительности прибора - наименьшее значение измеряемой величины, вызывающее различимое изменение показания прибора.
Вариация показаний - наибольшая возможная разность между отдельными повторными показаниями прибора, соответствующими одному и тому же значению измеряемой величины при неизменных внешних условиях. Вариация характеризует устойчивость показаний прибора. (В стрелочных приборах вариация показаний вызвана трением в опорах подвижной части прибора, люфтом оси рамки в подшипниках).
1.1. Классификация измерений.
Виды измерений. По способу нахождения числового значения физической величины измерения подразделяются на прямые, косвенные, совокупные и совместные.
Прямые измерения - измерения, при которых искомое значение величины находят непосредственно из опытных данных (например, измерение тока амперметром путем отсчета значения величины по шкале прибора).
Косвенные измерения - измерения, при которых искомое значение величины находят на основании известной зависимости между этой искомой величиной и другими величинами, определяемыми прямым измерением. (Например, определение значения определения резистора  "методом амперметра и вольтметра" по измеренным значениям напряжения
"методом амперметра и вольтметра" по измеренным значениям напряжения  тока
тока 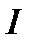 ).
).
Скорости  .
.
Совокупные измерения - одновременные измерения несколько одноименных величин, при которых искомое значение величин находят решением системы уравнений, составленных из результатов различных сочетаний этих величин.
Пример совокупного измерения: измерение сопротивлений обмоток двигателя с тремя обмотками соединенных звездой, путем измерений сопротивлений между различными вершинами звезды. Точка "0" недоступна для измерений.

Рис.6
 (12)
(12)
Совместные измерения - производимые одновременно измерения двух или нескольких не одноименных (различных) величин для нахождения зависимости между ними. Число уравнений должно быть равно числу подлежащих определению величин. Например, измерение, при котором сопротивление резистора  при температуре
при температуре  и его температурные коэффициенты
и его температурные коэффициенты  находят по данным прямых измерений сопротивления
находят по данным прямых измерений сопротивления  и температуры
и температуры 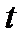 , выполненных при разных температурах, является совместным измерением:
, выполненных при разных температурах, является совместным измерением:
 (13)
(13)
Методы измерений. Различают два метода измерения: непосредственной оценки и сравнения с мерой.
Метод непосредственной оценки - метод измерений, в котором значение величины определяют непосредственно по отсчетному устройству измерительного прибора прямого действия, заранее градуированного в единицах измеряемой физической величины. Поскольку данный метод прост, он и наиболее распространен, хотя точность его не высока.
Метод сравнения с мерой - метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой. Этот метод по сравнению с методом непосредственной оценки более точен, но более сложен.
Разновидности метода сравнения имеют следующие модификации: противопоставления, дифференциальный, нулевой, замещения, совпадения.
Метод противопоставления - метод сравнения с мерой, в котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействует на прибор сравнения, с помощью которого устанавливается соотношение между этими величинами. Метод применяют при измерении ЭДС, напряжения, тока, частоты, параметров элементов схемы. Характерным является наличие двухисточников энергии. (Метод фигур Лиссажу…)
Дифференциальный метод - метод сравнения с мерой, в котором на измерительный прибор воздействует разность между измеряемой величиной и известной величиной, воспроизводимой мерой.
Точность метода возрастает с уменьшением разности между значениями сравниваемых величин. Метод применяют при измерении параметров цепей (сопротивления, индуктивности, емкости), напряжения и др. (Пример: приборы с использованием компараторов и т.д.).
Разновидность этого метода - нулевой метод - метод сравнения с мерой, в котором результирующий эффект воздействия величин на прибор сравнения доводит до нуля (мостовые моторы).
Метод замещения - метод сравнения с мерой, в котором измеряемую величину замещают известной величиной, воспроизводимой мерой. Метод замещения часто применяют при измерении параметров цепей (R,L,C).
Метод совпадения - метод сравнения с мерой, в котором разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадения отметок шкал или периодических сигналов. Метод применяют при измерении частот, интервалов времени. (Например, стробоскопический метод измерения частоты, числа оборотов вращения детали с помощью мигающей лампы) совпадение числа оборота метки с частотой вспышки стробоскопа.
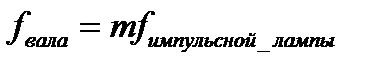
2.5 Единицы измерений.
Размер физической величины определяется соотношением  ,
,
где  - числовое значение этой величины,
- числовое значение этой величины,
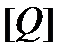 - единица измерения физической величины (принято писать в квадратных скобках!)
- единица измерения физической величины (принято писать в квадратных скобках!)
Это соотношение называется основным уравнением измерения, так как целью измерения, по существу, является определением числа  .
.
Обеспечение единства измерений предполагает, прежде всего, повсеместное использование общепринятых и строго определенных единиц физических величин.
Единицы физических величин подразделяются на основные и производные единицы.
Совокупность выбранных основных единиц и образованных с их помощью единиц производных называется системой единиц.
Правила, по которым тот или иной комплекс единиц выбирается в качестве основного, не могут быть обоснованы теоретически. Аргументом в пользу выбора может служить лишь эффективность и целесообразность использования данной системы. За историю развития естественных наук таких систем было предложено несколько (СГС, МТС. МКС и т.д.).
Для практических целей измерения в качестве основных величин и единиц следует выбирать такие, которые могут быть воспроизведены с наибольшей точностью.
В механике это длина, масса и время, в термодинамике - температура, в электродинамике и фотометрии - сила электрического тока и сила света, в электрохимии - количество вещества.
В октябре 1958 г. Международный комитет законодательной метрологии в г.Париж объявляет об установлении Международной системы единиц измерения - СИ (SI- фр.Systeme International). С 1января 1982 г. введен в действие ГОСТ8.417-81 (на основе СТСЭВ1052-78) "ГСИ. Единицы физических величин", в соответствии с которым осуществляется переход на Международную систему единиц СИ во всех областных наук, техники, народного хозяйства, а также в учебном процессе во всех учебных заведениях.
Основных единиц измерения семь:
Табл.1
| Величина | Обозначение размерности | Единица измерения | Обозначение | |
| русск. | междунар. | |||
| 1. Длина 2. Масса 3. Время 4. Сила электрического тока 5. Термодинамическая температура 6. Сила света 7. Количество вещества | L
M
T
I
 J
N
J
N
| метр килограмм секунда ампер кельин кандела(свеча) моль | м кг с А К кд моль | м kg s A K cd mol |
Введены также две дополнительные единицы:
Табл.2
| Величина | Единица измерения | Обозначение | Определение | |
| русск. | междунар. | |||
| Плоский угол | Радиан 
| рад | rad | Радиан равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу |
| Телесный угол | Стерадиан
(стере греч. - пространственный

| ср | sr | Стерадиан равен телесному углу с вершиной в центре сферы, вырезающему на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы. |
Производные единицы Международной системы, как правило, образуют с помощью простейших уравнений связи между физическими величинами, в которых числовые коэффициенты равны 1. Для образования производных единиц величины в уравнениях связи принимаются равными основным и дополнительным единицам СИ.
Пример: Единицу скорости образуют с помощью уравнения, определяющего скорость прямолинейно и равномерно движущейся точки
 , (15)
, (15)
где  - скорость,
- скорость,  - длина пройденного пути,
- длина пройденного пути,  - время движения точки.
- время движения точки.
Подстановка вместо  и
и  единиц СИ дает
единиц СИ дает

Следовательно, единицей скорости СИ является метр в секунду.
Таким образом для любой производной величины  может быть определена ее размерность (анг. Dimension [di'men
может быть определена ее размерность (анг. Dimension [di'men  эn]), отражающая ее связь с основными единицами системы, в виде
эn]), отражающая ее связь с основными единицами системы, в виде
 (16)
(16)
где 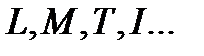 - полный набор основных единиц системы,
- полный набор основных единиц системы,
 - показатели степени для каждой конкретной производной физической величины находятся из уравнений, связывающий ее с основными величинами (часть этих показателей обычно оказывается равной нулю). Для рассмотренного выше примера
- показатели степени для каждой конкретной производной физической величины находятся из уравнений, связывающий ее с основными величинами (часть этих показателей обычно оказывается равной нулю). Для рассмотренного выше примера
 , т.е.
, т.е. 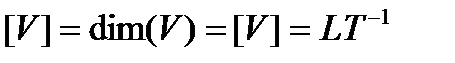
Соотношение (16) называется формулой размерности.
Некоторые производные единицы имеют собственные наименования, а другие обозначаются в виде произведения степеней других единиц, например:
Табл.3.
| Величина | Размерность | Наименование | Обозначение |
| Электрическая емкость Электрическое сопротивление Напряженность электрического поля Количество электричества (электрический заряд) Частота | 
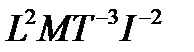


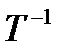
| Фарада Ом Вольт на метр Кулон герц | Ф Ом В/м Кл Гц |
Совместно с единицами системы СИ допускается использование кратных и дольных единиц, которые образуются путем добавления к названию единицы определенной приставки, означающей умножение данной единицы на 10n , где n - целое положительное (для кратных единиц) или отрицательное (для дальних единиц).
Табл.4.
| Множитель | Приставка | Обозначение | |
| русск. | Межд. | ||
| 1018 1015 1012 109 106 103 102 101 10-1 10-2 10-3 10-6 10-9 10-12 10-15 10-18 | экса пета тера гига мега кило гекто декабрь деци санти милли микро нано пико фемто атто | Э П Т Г М к г да д с м мк н п ф а | E
P
T
G
M
k
h
da
d
c
m
 n
p
f
a
n
p
f
a
|
Совместно с системой СИ допускается использование - там, где это целесообразно, - некоторых внесистемных единиц:
Пример: Табл.5
| Величина | Внесистемные единицы | Обозначение |
| Время | Минута, час, сутки | Мин, ч, сут. |
| Масса | тонна | т |
| Температура | Градус Цельсия
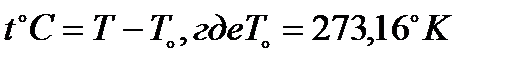 Градус Фаренгейта
Градус Фаренгейта
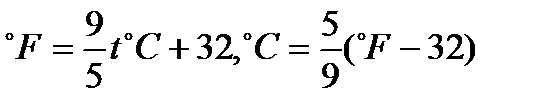
|  (Centigrade)
(Centigrade)
 (Fahrenheit)
(Fahrenheit)
|

|
Кроме рассмотренных видов единиц широко применяются относительные и логарифмические величины. Они представляют собой соответственно отношение двух одноименных величин и логарифм этого отношения.
К относительным величинам, в частности, относятся атомные и молекулярные массы химических элементов.
Относительные величины могут выражаться 9% уксус (9 г уксуса в 100 г раствора) в безразмерных единицах, в процентах (1% Þ 0,01) или в промилле (1‰ Þ0,001 Þ 0,1%).
Значения логарифмических величин выражается: в неперах (Нп) согласно формуле
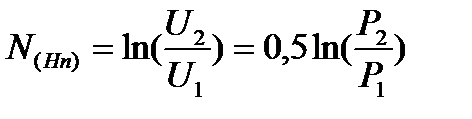 (17)
(17)
-в телеграфии затухание электрического сигнала
или в белах (Б)
 -в электронике, акустике. (18)
-в электронике, акустике. (18)
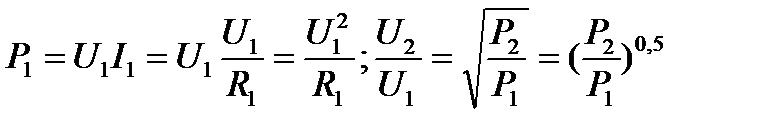

Если 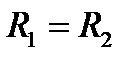 , то
, то 
В этих отношениях  и
и  - энергетические величины (мощность, энергия, плотность энергии…),
- энергетические величины (мощность, энергия, плотность энергии…), 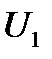 и
и 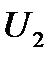 - силовые величины (напряжение, ток, напряженность поля, звуковое давление и т.д.)
- силовые величины (напряжение, ток, напряженность поля, звуковое давление и т.д.)
Если  а
а  , то
, то 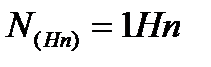
Если  , а
, а 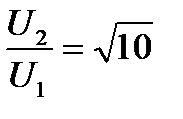 , то
, то 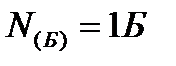
В радиотехнике, электронике и акустике логарифмические величины чаще выражают в децибелах (1дБ=0,1Б; 1Б=10дБ).
 (19)
(19)
2. Основы теории погрешностей и обработки результатов измерения.
2.1. Виды погрешностей (классификация погрешностей) по следующим признакам:
а) по способу оценки - абсолютная погрешность
- относительная погрешность
б) в зависимости от причины возникновения
- методическая
- инструментальная
- от внешних условий
- субъективная
в) от характера проявления - систематическая
- случайная
г) по характеру зависимости от измеряемой величины
- аддитивная
- мультипликативная.
При любом измерении неизбежны обусловленные разнообразными причинами отклонения результатов измерения от истинного значения измеряемой величины.
Истинные значения физических величин - это значения, идеальным образом отражающие свойства данного объекта.
Погрешность измерения - отклонение результата измерения от истинного значения измеряемой величины.
Различают по способу оценки абсолютную и относительную погрешность измерения.
Абсолютная погрешность измерения  равна разности между результатом измерения
равна разности между результатом измерения  и истинным значением измеряемой величины
и истинным значением измеряемой величины 
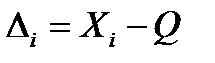 (20)
(20)
Но поскольку истинное значение  измеряемой величины неизвестно, то вместо истинного значения подставляют так называемое действительное значение
измеряемой величины неизвестно, то вместо истинного значения подставляют так называемое действительное значение  , найденное экспериментально и настолько приближающееся к истинному, что для данной цели оно может быть использовано вместо него
, найденное экспериментально и настолько приближающееся к истинному, что для данной цели оно может быть использовано вместо него
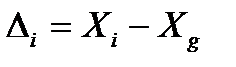 (21)
(21)
Относительная погрешность измерения  представляет собой отношение (в процентах) абсолютной погрешности измерения к истинному значению измеряемой величины или действительному значению
представляет собой отношение (в процентах) абсолютной погрешности измерения к истинному значению измеряемой величины или действительному значению
 (22)
(22)
Абсолютная погрешность измерения выражается в тех же единицах, что и измеряемая величина, относительная погрешность безразмерна.
Существует также такой качественный показатель измерения, как точность измерения, отражающий
 (23)
(23)
близость результата к истинному значению изм. величины.
Пример: Если в результате измерения установлено, что относительнаяпогрешность нестабильности частоты генератора электрических колебаний

то точность поддержания частоты  .
.
Погрешности классифицируются по следующим признакам:
В зависимости от причин возникновения различаются: погрешности метода измерений (методическая погрешность), возникающая из-за несовершенства метода, принципа или методики измерения; инструментальные погрешности, зависящие от погрешностей средств измерения; погрешности, вызванные изменением внешних условий; субъективные погрешности, возникающие из-за недостаточно точного отсчитывания показаний средств измерения. От таких погрешностей нужно отличать промахи - неверные результаты измерения, получаемые в результате субъективной ошибки в измерении. При отработке результатов многократных наблюдений промахи должны быть выявлены и исключены из рассмотрения.
В зависимости от характера проявления (закономерности проявления) при повторении измерений различаются следующие виды погрешностей:
Систематическая погрешность  - это составляющая погрешности, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины (например, погрешность градуировки шкалы, температурная погрешность, погрешность установки статического и электрического "нуля" стрелочного прибора и т.д.).
- это составляющая погрешности, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины (например, погрешность градуировки шкалы, температурная погрешность, погрешность установки статического и электрического "нуля" стрелочного прибора и т.д.).
Систематическая погрешность принципиально предсказуема и если она определена достаточно точно, то может быть исключена (вручную или автоматически) введением поправки (равной систематической погрешности с обратным знаком) или поправочного множителя.
Случайная погрешность  - это составляющая погрешности, которая изменяется случайным образом при повторных измерениях одной и той же величины, Такого рода погрешность является следствием случайных процессов (закономерности которых установить не удается) в измерительных цепях и во (влияющей) внешней среде.
- это составляющая погрешности, которая изменяется случайным образом при повторных измерениях одной и той же величины, Такого рода погрешность является следствием случайных процессов (закономерности которых установить не удается) в измерительных цепях и во (влияющей) внешней среде.
Пример, погрешность, обусловленная собственными шумами средств измерений или дискретным характером показаний цифрового прибора.
Принципиальным отличием случайной погрешности от систематической является то, что ее значение для единичных наблюдений не может бытьпредсказано, Путем многократных измерений одной и той же величины и статистической обработки результатов значение случайной погрешности может быть найдено вероятностными методами.
В общем случае погрешность измерения состоит из суммы систематической и случайной погрешности
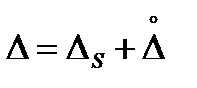 (24)
(24)
Среди погрешностей средств измерения (инструментальных) различаются:
- статистическая погрешность  , имеющая место при измерении постоянной величины (или изменяющейся настолько медленно, что инерционные свойства средств измерения при этом не появляются);
, имеющая место при измерении постоянной величины (или изменяющейся настолько медленно, что инерционные свойства средств измерения при этом не появляются);
- динамическая погрешность  , возникающая при измерении переменных величин за счет инерционных свойств средств измерений - разность между погрешностью при измерении переменной во времени величины и статистической погрешностью;
, возникающая при измерении переменных величин за счет инерционных свойств средств измерений - разность между погрешностью при измерении переменной во времени величины и статистической погрешностью;
- основная погрешность  - погрешность в нормальных условиях (устанавливаемых в стандартах и технических условиях на средства измерения данного вида);
- погрешность в нормальных условиях (устанавливаемых в стандартах и технических условиях на средства измерения данного вида);
- дополнительная погрешность  - изменение погрешности вследствие отклонения одной из влияющих величин от нормального значения (например,изменения температуры окружающей среды от нормы);
- изменение погрешности вследствие отклонения одной из влияющих величин от нормального значения (например,изменения температуры окружающей среды от нормы);
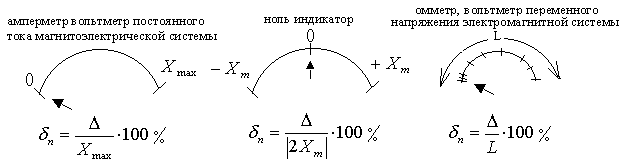
- приведенная погрешность - выраженное в процентах отношение абсолютной погрешности измерительного прибора к нормирующему значению, за которое условно принимается либо верхний предел измерений, либо диапазон измерений, либо длина шкалы и т.п. (см.рис.7)