1. Какую систему обыкновенных дифференциальных уравнений называют автономной?
Система обыкновенных дифференциальных уравнений называется автономной или динамической, если независимое переменное явно не входит в систему.
Общий вид автономной системы из 
уравнений в нормальной форме следующий:
или подробнее
.
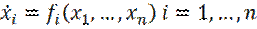2. Какова связь между фазовой траекторией автономной системы и соответствующей интегральной кривой этой системы?
Пусть 
есть решение автономной системы 
тогда множество точек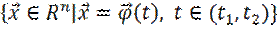 
является кривой в пространстве 
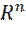. Эту кривую называют фазовой траекторией, а пространство 
, в котором расположены фазовые траектории – фазовым пространством автономной системы. Интегральные кривые системы изображаются в 
-мерном пространстве 
с координатами 
. Соответствующая фазовая траектория является проекцией интегральной кривой на фазовое пространство, параллельной оси 
.
3. Рассмотрим автономную систему из уравнений 
, для которой выполнены условия основной теоремы существования и единственности решения. Пусть 
функция, заданная в фазовом пространстве этой системы и непрерывно дифференцируемая там. Дать определение производной этой функции в силу автономной системы.
Производная функции определяется равенством
,
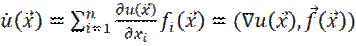где 
– градиент функции . Производная в силу системы называется также производной по направлению векторного поля 
или производной Ли.
4. Пусть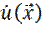 
-- производная в силу системы и 
в некоторой области фазового пространства 
. Тогда функция не убывает (не возрастает) вдоль любой фазовой траектории системы, лежащей в области . Как называют функцию , если ее производная в силу системы тождественно равна нулю?
Функция называется первым интегралом автономной системы 
, если эта функция постоянна вдоль каждой траектории этой системы. Таким образом, если 
– решение системы, то функция 
при всех . Для того, чтобы функция 
была первым интегралом системы 
, необходимо и достаточно, чтобы ее производная в силу этой системы была равна нулю: 
.
5. Дать определение устойчивости по Ляпунову положения равновесия автономной системы.
Рассмотрим автономную систему из уравнений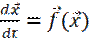 
. Обозначим 
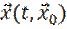решение этой системы с начальными данными 
.
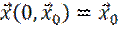Положение равновесия 
называется устойчивым по Ляпунову, если:
· существует 
такое, что если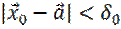 
, то решение 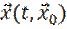существует при 
;
· для всякого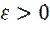 
существует 
такое, что если 
, то 
при всех 
.
Это означает, что если в начальный момент времени изображающая точка находится достаточно близко к положению равновесия, то и во все последующие моменты времени, двигаясь по траектории, точка будет оставаться в близи положения равновесия.
6. Дать определение асимптотической устойчивости положения равновесия автономной системы.
Положение равновесия называется асимптотически устойчивым, если оно устойчиво по Ляпунову и если 
при достаточно малых 
.
Это означает, что если точку немного сдвинуть их положения равновесия, то она с ростом времени будет стремиться вернуться в положение равновесия.
7. Пусть автономная система имеет положение равновесия , т. е. 
. Каким образом можно заменой переменной свести исследование устойчивости положения равновесия этой системы к исследованию устойчивости начала координат другой системы, которую называют приведенной или, следуя Ляпунову, системой уравнений возмущенного движения.
Выполним замену переменной 
, где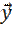 
отклонение фазового вектора 
от положения равновесия 
. В новых переменных уравнение будет иметь вид 
и будет иметь положение равновесия 
, соответствующее положению равновесия исходной системы. При исследовании устойчивости положения равновесия его называют невозмущенным движением, вектор называют возмущением, а уравнение -- уравнением возмущенного движения.
8. При исследовании устойчивости положения равновесия автономной системы прямым методом Ляпунова рассматривают некоторые функции, не зависящие от времени, определенные в некоторой окрестности положения равновесия приведенной системы и обладающие непрерывными частными производными. В каких случаях такие функции называют знакоопределенными? В каких случаях такие функции называют знакопостоянными? В каких случаях такие функции называют знакопеременными?
Функция 
называется знакоопределенной (определенно-положительной или определенно отрицательной), если она при 
, где 
-- достаточно малое положительное число, может принимать значения только одного определенного знака и обращаться в нуль толькопри 
.
Функция называется знакопостоянной (положительной или отрицательной), если она при , где -- достаточно малое положительное число, может принимать значения только одного определенного знака, но может обращаться в нуль и при 
.
Функция 
называется знакопеременной, если в любой, сколь угодно малой, окрестности начала координат принимает как положительные, так и отрицательные значения.
Например, функция 
-- определенно-положительная, а функция 
-- положительна.
9. Доказать знакоопределенность функции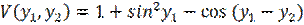 
.
Разложим функцию 
в ряд в окрестности начала координат. Так как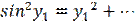 
и 
, то 
Таким образом
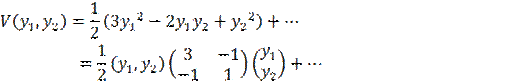
Применим критерий Сильвестра для определения положительной определенности квадратичной формы в разложении функции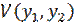 
.
Для того чтобы квадратичная форма с вещественными коэффициентами была определенно-положительной, необходимо и достаточно, чтобы все главные диагональные миноры 
матрицы ее коэффициентов были положительны.
В нашем случае 
и согласно критерию Сильвестра квадратичная форма 
-- определенно-положительна. Отсюда заключаем, что функция 
в малой окрестности начала координат определенно-положительна.
10. Сформулировать теорему Ляпунова об устойчивости невозмущенного движения и применить ее для исследования устойчивости положения равновесия системы
В качестве функции Ляпунова взять функцию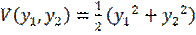 
.
Если для дифференциальных уравнений возмущенного движения можно найти знакоопределенную функцию 
, производная которой 
в силу этих уравнений была бы знакопостоянной противоположного знака с , или тождественно равной нулю, то невозмущенное движение устойчиво.
Найдем производную функции 
в силу системы
.
Функция -- определенно-положительна, а ее производная 
-- отрицательная функция. На основании теоремы Ляпунова можно утверждать, что невозмущенное движение 
устойчиво.
11. Сформулировать теорему Ляпунова об асимптотической устойчивости невозмущенного движения и применить ее для исследования устойчивости положения равновесия системы
В качестве функции Ляпунова взять функцию 
.
Если для дифференциальных уравнений возмущенного движения можно найти знакоопределенную функцию , производная которой в силу этих уравнений была бы знакоопределенной функцией противоположного знака с 
, то невозмущенное движение асимптотически устойчиво.
Квадратичная форма 
определенно-положительна. Это было установлено по критерию Сильвестра в ответе на вопрос с номером 20. Производная этой формы в силу системы имеет вид 
.
Для того чтобы квадратичная форма с вещественными коэффициентами была определенно-отрицательной, необходимо и достаточно, чтобы все главные диагональные миноры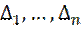 
матрицы ее коэффициентов последовательно меняли свой знак:
.
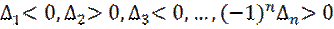В нашем случае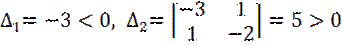 
, т. е. – определенно-отрицательная функция относительно 
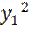и 
, следовательно, и относительно 
и .
Функция -- определенно-положительна, а ее производная – определенно-отрицательная функция. На основании теоремы Ляпунова об асимптотической устойчивости можно утверждать, что невозмущенное движение асимптотически устойчиво.
12. Сформулировать теорему Ляпунова о неустойчивости движения и применить ее к доказательству неустойчивости положения равновесия уравнения 
, выбрав в качестве функции Ляпунова 
.
Если дифференциальные уравнения возмущенного движения позволяют найти функцию , которая обладала бы в силу этих уравнений знакоопределенной производной и могла бы принимать в окрестности нуля значения одного знака с , то невозмущенное движение неустойчиво.
Производная функции в силу уравнения положительно-определена 
. Сама функция 
принимает положительные значения в сколь угодно малой окрестности положения равновесия (она – положительно определена). Следовательно, положение равновесия 
является неустойчивым.
13. Рассмотрим линейную автономную систему из уравнений 
. Эта система имеет положение равновесия . Так как такая система интегрируется, вопрос об устойчивости этого положения равновесия полностью исследован. Сформулировать необходимое и достаточное условие асимптотической устойчивости положения равновесия этой системы.
Положение равновесия системы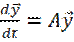 
асимптотически устойчиво тогда и только тогда, когда вещественные части всех собственных значений матрицы 
отрицательны.
14. Выше мы говорили об устойчивости положения равновесия автономной системы. Рассмотрим произвольное решение 
системы дифференциальных уравнений 
. Дать определение устойчивости этого решения по Ляпунову.
Решение называется устойчивым по Ляпунову, если для любых 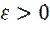и 
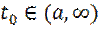существует 
такое, что
· все решения 
системы 
, удовлетворяющие условию 
, определены в промежутке 
;
· для этих решений справедливо неравенство 
при 
.
15. Дать определение асимптотической устойчивости решения системы дифференциальных уравнений.
Решение называется асимптотически устойчивым при 
, если
· это решение устойчиво по Ляпунову
· для любого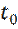 
существует 
такое, что из неравенства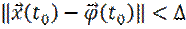 
следует 
.
Если решение системы с непрерывной правой частью устойчиво для какого-нибудь фиксированного момента времени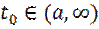 
, то оно будет устойчивым для любого другого момента, т. е. будет устойчивым в смысле данного выше определения. Таким образом можно ограничиваться проверкой устойчивости решения лишь для некоторого начального момента 
.
16. Понятие приведенной системы или системы уравнений возмущенного движения применяется не только при исследовании устойчивости положения равновесия автономной системы, но и при исследовании устойчивости произвольного решения системы дифференциальных уравнений 
. Дать определение приведенной системы.
Пусть решение системы , устойчивость которого требуется исследовать (невозмущенное движение). Положим 
, т. е. 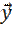есть отклонение решения 
от решения 
. Так как
,
то для для 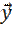получаем дифференциальное уравнение
.
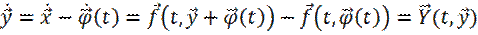Так как 
, система 
имеет тривиальное решение , которое соответствует исходному 
(невозмущенному движению). Систему уравнений называют приведенной или системой уравнений возмущенного движения.
17. Рассмотрим линейную систему дифференциальных уравнений
.
Показать, что все ее решения либо устойчивы, либо неустойчивы.
Пусть решение системы
,
устойчивость которого требуется исследовать (невозмущенное движение). Положим , т. е. 
есть отклонение решения от решения . Тогда
.
Приведенное уравнение имеет вид 
. Если положение равновесия этой однородной линейной системы устойчиво, то любое решение исходной системы устойчиво. Линейную систему называют устойчивой, если все ее решения устойчивы.
18. Найти решение задачи Коши
.
Исследовать устойчивость этого решения.
Найдем собственные значения матрицы системы. Они являются корнями характеристического полинома
.
Собственные числа 
и 
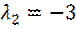отрицательны. Следовательно любое решение этой системы асимптотически устойчиво.
Собственный вектор, отвечающий собственному числу , является решением алгебраической системы 
, т. е.
.
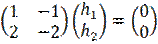Можно взять ненулевое решение 
.
Собственный вектор, отвечающий собственному числу 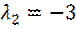, является решением алгебраической системы 
, т. е.
.
Можно взять ненулевое решение 
.
Построим неособенную матрицу
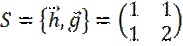
и найдем обратную к ней
.
Решение начальной задачи можно теперь подсчитать следующим образом:
.
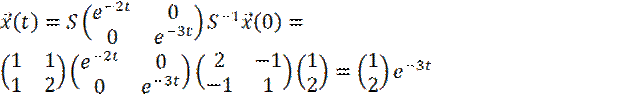