Земельный фонд области, в соответствии с целевым использованием, распределен по категориям земель, ведущая из которых остается категория сельскохозяйственного назначения.
В данной работе проведен трендовый анализ земель сельскохозяйственного назначения и земель запаса.
Прогнозирование экономических показателей осуществляется на основе метода линейной регрессии; если прогнозирование показателей происходит во времени, мы имеем дело с трендовым анализом.
В случае простой регрессии определяется степень зависимости между двумя показателями, один из которых является независимым показателем – фактором «Х» (время), а другой – зависимым фактором «Y» (площадь земель). Эта зависимость характеризуется функцией 3.1:
Y = f (t), (3.1)
Трендовый анализ состоит из:
- корреляционного анализа, предназначенного для изучения тесноты связи между факторным (временным) и результативным показателем;
- регрессионного анализа – для нахождения уравнения регрессии, оценки его точности и надежности (репрезентативности);
- прогноза результативного показателя на основе полученной модели уравнения регрессии.
Исходные данные для проведения трендового анализа приведены в
таблице 3.1.
Таблица 3.1
Исходные данные для проведения трендового анализа
| Годы | Площадь с/х земель, тыс.га | Земли запаса, тыс.га |
| 4546,5 | 16640,7 | |
| 4590,3 | 16614,7 | |
| 5024,8 | 16075,4 | |
| 5492,1 | 15611,3 | |
| 6038,2 | 15057,7 | |
| 7037,4 | 14067,4 | |
| 7733,8 | 13330,2 | |
| 8672,6 | 12354,7 | |
| 9597,7 | 11900,2 | |
| 9925,5 | 11214,5 | |
| 9944,1 | ||
| 10271,1 | ||
| 10273,9 | 10653,1 | |
| 10342,1 | 10587,2 |
Корреляционный анализ показывает тесноту связи между варьирующими признаками, определяет неизвестные причинные связи (причинный характер которых должен быть выяснен с помощью теоретического анализа) и оценку факторов, оказывающих наибольшее влияние на результативный признак.
Регрессионный анализ помогает выбрать тип модели (формы связи), установить степень влияния независимых переменных на зависимую и определить расчётные значения зависимой переменной (функции регрессии). Эти методы используются комплексно.
Уравнение регрессии определяется с помощью метода наименьших квадратов (системы нормальных уравнений), либо параболическим интерполированием. Для линейной зависимости, используемой в данной работе, система нормальных уравнений 3.2:
(3.2)
,
где n – число условных уравнений, равное числу фактических пар связей между (Y) и (X).
Полученные коэффициенты подставляем в уравнение регрессии, затем оно проверяется на надежность (репрезентативность) при помощи определения нескольких основных оценок надежности:
- коэффициент корреляции r (для линейной регрессии) – определяет тесноту связи между исследуемыми показателями:
; 
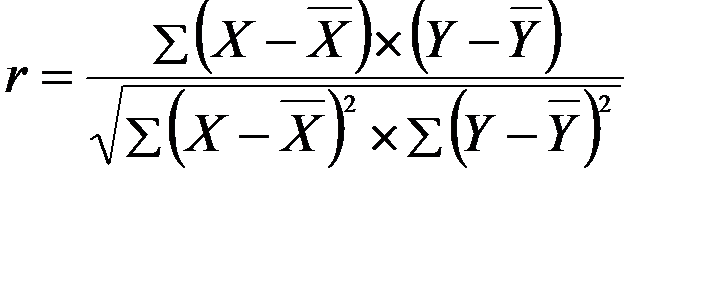, (3.3)
где X,Y – текущие значения наблюдаемых величин;
, 
- средние значения этих величин.
Практически, если (r) не превышают величины 0,25, то это свидетельствует о слабой связи между выбранными показателями. Обычно при 
говорят о малой зависимости, при 0,3<r<0,6 – о средней и при r> 0,6 – о большой (существенной) зависимости;
- коэффициент детерминации r2 – показывает в какой степени факторный показатель X находится в зависимости от результативного – Y (3.4).
- t – критерий Стьюдента - определяет надежность коэффициента корреляции (формула (3.5)).
При небольшом числе наблюдений считается надежными, значимыми, если критерий надежности (критерий Стьюдента) - 
(для двух степеней свободы при 5% погрешности).
, (3.4)
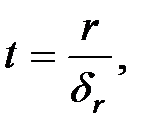(3.5)
где δr,δη – соответственно средняя квадратичная ошибка (r) или (η).
- надежность уравнения регрессии оценивается по F – критерию Фишера. Расчетные значения данных критериев должны быть >> табличных (по соответствующим таблицам статистических справочников).
Главным этапом построения регрессионной модели (уравнения регрессии) является установление в анализе исходной информации математической функции. При этом из множества функций выбирается такая, которая лучше других выражает реально существующие связи между анализируемыми признаками.
Трендовый анализ может быть проведен вручную, либо с использованием ПК (с помощью электронных таблиц Excel или прикладной программы).
Проведенный анализ исходной информации по нахождению оптимальной математической функции показал, что наиболее точно данные зависимости описывает полином 2-ой степени.
Проведение трендового анализа представлено на рисунке 3.1.
Рисунок 3.1 Построение полиномиальных трендов
Получим уравнения регрессии:
- для площадей с/х земель: Y = -20,738x2 + 847,99x + 2964,3;
- для земель запаса: Y = 18,201x2 – 825,35x + 18145.
Коэффициенты корреляции и детерминации близки к 1, следовательно, прогноз будет достоверным.
На основе полученных уравнений рассчитаем прогнозные значения на период с 2015-2018гг.
Прогнозные значения площадей представлены в таблице 3.2.
Таблица 3.2
Прогноз площадей с/х земель и земель запаса на период с 2015-18гг по полиномиальному тренду
| Годы | Прогнозируемая площадь с/х земель, тыс.Га | Прогнозируемая площадь земель запаса, тыс.Га |
| 11018,100 | 9859,975 | |
| 11223,212 | 9598,856 | |
| 11386,848 | 9374,139 | |
| 11509,008 | 9185,824 |
Таким образом, по прогнозным значениям с/х земель прослеживается постоянный прирост из года в год и в 2018 году по сравнению с 2014 годом общий прирост составит 1166,908 тыс.га или 11,28%. Прогнозные значения земель запаса показали постоянное снижение и в 2018 году по сравнению с 2014 годом общее снижение составит 1401,376 тыс.га или 13,24%.
Можно сделать вывод о том, что площадь земель запаса сократится немного больше – на 2%, чем увеличатся площади с/х земель.