Обобщающие характеристики совокупностей
Анализ статистических совокупностей включает в себя: построение рядов распределения; графическое представление распределения; определение характеристик центра распределения, показателей вариации.
Рядами распределения называют числовые ряды, характеризующие структуру совокупности по некоторому признаку. Ряд распределения может быть получен в результате структурной группировки. Ряд распределения, образованный по количественному признаку (он называется вариационным рядом), может быть дискретным, если значения признака выражены целыми числами и каждая варианта представлена в вариационном ряде отдельной группой, или интервальным (непрерывным), если значения признака выражены вещественными числами или число вариант признака достаточно велико.
Элементами ряда распределения являются:
xi – варианта – отдельное, возможное значение признака
i = 1, 2,..., K, где K – число значений признака;
fi – частота – численность отдельных групп соответствующих значений признаков;
N – объём совокупности – общее число элементов совокупности;
qi – частость – доля отдельных групп во всей совокупности.
При этом
 .
.
Вариационный ряд оформляется в виде таблицы, где в первой графе указываются варианты (интервалы) значений признака, а в следующих графах частота, накопленная частота.
Макет таблицы может выглядеть следующим образом:
Таблица № – Переход к дискретному ряду распределения
| Границы интервалов признака-фактора (единица измерения) | Середины интервалов хi | Частота fi | Накопленная частота fнак | |
| ... | ... | ... | ||
| ... | ... | ... | ||
| ... | ... | ... | ||
| Итого | Общее число элементов совокупности | - |
Ряд распределения в целом характеризует структуру совокупности по данному признаку. Однако для описания распределения совокупность могут использоваться и кумулятивные ряды, т. е. ряды накопленных частот (или частостей.
Накопленная частота (частость ) данного значения признака - это число (доля) элементов совокупности, индивидуальные значения признака которых не превышают данного.
Первым этапом изучения вариационного ряда является его графическое изображение. Способы построения графиков для разных видов рядов распределения различны.
Изображением дискретного вариационного ряда распределения является полигон. При его построении в системе координат по оси абсцисс откладываются варианты (xi), по оси ординат - частоты (частости) fi, затем отмечают точки с координатами (xi;fi), которые последовательно соединяются отрезками прямой.
Интервальный ряд распределения изображается графически в виде гистограммы. При её построении на оси абсцисс откладывают интервалы ряда. Над осью абсцисс строятся прямоугольники, основанием которых является интервал, а высота - соответствующая этому интервалу частота, частость.
Изображением ряда накопленных частот служит кумулята. Накопленные частоты наносятся в системе координат в виде ординат для границ интервалов; соединяя нанесенные точки отрезками прямых, получаем кумуляту.
Вторым этапом изучения вариационного ряда является определение характеристик центра распределения. Характеристика центра распределения представляет собой такую величину, которая в некотором отношении характерна для данного распределения и является его центральной величиной.
К характеристикам центра распределения относятся:
1. Средняя арифметическая
2. Медиана
3. Мода.
Макет расчетной таблицы для вычисления характеристик ряда может выглядеть следующим образом:
Таблица № – Расчетная таблица для вычисления характеристики ряда
| Границы интервалов признака-фактора (единица измерения) | Середины интервалов хi | Частота fi | хi fi | хi2 fi | |
| ... | ... | ... | |||
| ... | ... | ... | |||
| ... | ... | ... | |||
| Итого | S | n=50 |
1. Для не сгруппированных данных рассчитывают среднюю арифметическую простую
 .
.
Для сгруппированных данных, представленных в вариационном ряду средняя арифметическая (` x) определяется как
 ,
,
где хi – варианта или середина интервала i -й группы,
fi – частота или вес i -й группы.
Если ряд дискретный, то каждое значение признака представлено. Если же ряд интервальный, то его нужно превратить в условно дискретный: в качестве группового значения xi для каждого интервала вычисляется его середина.
2. Медиана (Me[ x ]) – это такое значение признака, которое делит объём совокупности пополам в том смысле, что число элементов совокупности с индивидуальными значениями признака, меньшими медианы, равна числу элементов совокупности с индивидуальными значениями больше медианы.
Численное значение медианы можно определить по ряду накопленных частот. Накопленная частота для Me[ x ] равна половине объёма совокупности
F (Me[ x ]) = N /2;
Имея ряд накопленных частот, можно вычислить, при каком значении признака накопленная частота равна половине объёма совокупности.
Для интервального ряда в этом случае определяется только интервал в котором будет находиться Me[ x ], само значение приближённо можно определить как
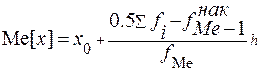 ,
,
где x 0 – нижняя граница интервала интервала, содержащего медиану;
f Ме– частота того интервала, в котором расположена медиана;
f Ме-1нак – накопленная частота предыдущего интервала;
N – объём совокупности;
h – шаг (величина интервала)
3. Мода (Mo[ x ]) – наиболее часто встречающееся значение признака в совокупности.
Для дискретного ряда — это то значение, которому соответствует наибольшая частота распределения.
Для интервального ряда вначале определяется интервал, содержащий моду, тот, которому соответствует наибольшая плотность распределения. Затем приближённо определяется численное значение моды.
Если ряд равноинтервальный, то используется формула
 ,
,
где x 0 – начало интервала, содержащего моду;
DMo – величина интервала, содержащего моду;
fM o – частота того интервала, в котором расположена мода;
f Mo-1 – частота интервала, предшествующего модальному;
f Mo+1 – частота интервала, следующего за модальным.