Местное сопротивление, при котором труба постепенно расширяется, называется диффузором.

Лекция № 12.

Теорема импульса.

Пусть имеется некоторый поток жидкости в сужающемся канале с расходом между сечениями (1-1) и (2-2) равным Q. Движение считаем установившимся. За время dt этот участок переместится в положение, определяемое сечениями (1’-1’) и (2’-2’). Канал – неподвижный и недеформируемый.

Будем считать, что:

1) жидкость несжимаема;

2) движение установившееся;

3) имеем одномерную модель потока с равномерным распределением скоростей по сечению.

Т.к. от сечения (1-1) до сечения (2-2) произошло изменение скоростей, то изменилось и количество движения (импульс сил), т.е. на поток действовали силы.

Обозначим: К – количество движения; ΣР – сумма всех внешних сил;

Тогда, dK = ΣP∙dt; где или

. Так как, , то получаем:

- теорема импульса, где ρQυ –секундное количество движения потока в данном сечении.

Приращение секундного количества движения потока в канале равно сумме действующих на него внешних сил.

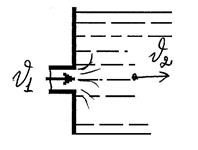
Внезапное расширение канала.

Характер протекания процесса:

1) Происходит инерционный отрыв на кромке, образованной уступом.

2) Постепенное растекание струи (поток отрывается от стенок канала, но расширяется постепенно).

3) Образование вихревой или водоворотной зоны, т.к.в сечении 1’ р₁^’ > р₁ => у стенок жидкость течёт в другую сторону.

На участке (1-1’) проявляются два вида движения – циркуляционное (частицы движутся по замкнутому контуру) и транзитное (частицы движутся прямо).

4) На участке стабилизации потока происходит размывание вихрей и выравнивание осреднённых скоростей (здесь происходит интенсивный переход энергии в тепло).

5) Выравнивание скоростей приводит к изменению давлений (т.е. р₂ > р₁) и к уменьшению количества движения потока.

6) Стабилизация потока происходит на длине – L ≈ 10∙d₂.

При расчёте потока будем использовать следующие соотношения:

I. Уравнение постоянства расхода - .

II. Уравнение сохранения энергии (уравнение Бернулли):

z₁ = z₂ = 0 (т.к. плоскость отсчёта совпадает с осью); α₁ = α₂ = 1 (турб. режим), тогда

(1)

III. Теорему импульса: .

При учёте всех внешних сил Р имеем ввиду, что есть нормальные силы (обусловлены действием внутренней поверхности канала на жидкость) и силы трения (из-за наличия касательных напряжений).

Ввиду малости – силами трения пренебрежём:

- так как участок деформации потока относительно мал;

- имеется взаимная компенсация τ₁ и τ₂.

 

В дальнейшем будем оперировать только силами давления, причём сила Р₁ равна: Р₁ =р₁∙F₂. Тогда

или .

Разделим обе части равенства на , получим:

- формула справедлива лишь для турбулентного режима.

Из уравнения (1), принимая во внимание полученную формулу, получаем:

В итоге имеем: 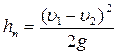- Формула Борда.

Потеря напора при внезапном расширении русла равна скоростному напору, определённому по разности скоростей до и после расширения.

С учётом ур. неразр., что скорость в широком сечении равна: 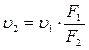, имеем:

, т.е. ,

где ζ_вр1 – коэффициент потерь напора при внезапном расширении канала.

 

Через скорость в узком сечении , получим:

, т.е. ,

где ζ_вр2 – коэффициент потерь напора при внезапном расширении канала.

Частный случай. В случае истечения жидкости из ограниченного объёма в неограниченный объём (т.е. F₂ ® ¥, υ₂ ® 0), имеем:

 

, так как .

Диффузоры.

Местное сопротивление, при котором труба постепенно расширяется, называется диффузором.

Течение жидкости в диффузоре сопровождается уменьшением скорости и увеличением давления, происходит преобразование кинетической энергии жидкости в энергию давления.

Слои жидкости, прилегающие к стенкам, обладают столь малой кинетической энергией, что подчас оказываются не в состоянии преодолевать повышенное давление, поэтому они останавливаются или даже начинают двигаться обратно (вид А на рисунке).

Основной поток наталкивается на эти противотоки, возникают вихреобразования и отрыв потока от стенки:

Вид А:

Интенсивность этих явлений возрастает с увеличением угла расширения диффузора.

Основная задача при проектировании и эксплуатации потока обеспечить безотрывное движение жидкости на длине L.

В хорошем диффузоре гидравлические потери напора на порядок меньше, чем при внезапном расширении. Потери напора в диффузоре равны сумме потерь на трение и потерь, обусловленных расширением потока:

,

где h_тр – потери напора на преодоление трения по длине диффузора;

h_расш – потери напора при расширении потока.

 

Однако, часто за основу определения потерь напора в диффузоре, принимают формулу Борда:

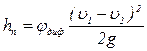, где φ_диф – безразмерный коэффициент сопротивления диффузора.

Коэффициент диффузора φ_диф определяется экспериментально и зависит главным образом от:

- угла раскрытия Ө°;

- от отношения площадей ;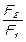

- относительной гладкости .

График зависимости коэффициента диффузора - φ_диф= f (Ө) имеет следующий вид:

На графике имеем:

- участок А – в потоке доминируют потери на трение (п ри увеличении угла раскрытия диффузора Ө° - уменьшается L и уменьшаются потери.

- участок В - нарастают потери из-за отрыва, вихреобразования и удара;

- участок С - полный отрыв, т.е. х ≈ 0.

На практике в целях сокращения длины диффузора при заданном отношении обычно принимают: Ө_опт = 6° - 8°, а φ_{диф.мин}= 0,1 – 0,2.

Диффузор устанавливают для уменьшения потерь, возникающих при переходе от меньшего диаметра трубы к большему.