ВОПРОСЫК ЭКЗАМЕНУ ПО КУРСУ «Теория вероятностей ».
1. Предмет теории вероятностей. Понятия массового случайного явления, случайного эксперимента, случайного события. Свойство статистической устойчивости исходов случайного эксперимента, пример такого эксперимента.
2. Элементарное событие. Пространство элементарных событий. Случайное событие. Достоверное и невозможное события. Представление событий в виде диаграмм Эйлера-Венна.
3. Действия над случайными событиями (произведение, сумма, разность, дополнение), их определения и геометрическая иллюстрация с помощью диаграмм Эйлера-Венна. Совместные и несовместные, противоположные события.
4. Равновозможные события. Классическое определение вероятности, её свойства.
5. Правила суммы и произведения комбинаторики. Сочетания, размещения и перестановки, подсчёт их числа.
6. Геометрическое определение вероятности. Задача о встрече.
7. Частота, относительная частота появления события. Статистическое определение вероятности.
8.  -алгебра событий. Аксиоматическое определение вероятности. Вероятностное пространство.
-алгебра событий. Аксиоматическое определение вероятности. Вероятностное пространство.
9. Основные свойства вероятности. Формулы сложения вероятностей.
10. Условная вероятность события. Зависимые и независимые события. Формулы умножения вероятностей.
11. Полная группа событий, гипотезы. Формулы полной вероятности и Байеса, их применение.
12. Повторные испытания. Схема Бернулли. Формула Бернулли. Формулы для вероятности того, что в  испытаниях по схеме Бернулли число успехов будет заключено в пределах от
испытаниях по схеме Бернулли число успехов будет заключено в пределах от  до
до  ; произойдёт хотя бы один успех.
; произойдёт хотя бы один успех.
13. Приближённые формула Пуассона и интегральная формула Муавра-Лапласа, условия их применения.
14. Наивероятнейшее число успехов в  испытаниях по схеме Бернулли, его нахождение.
испытаниях по схеме Бернулли, его нахождение.
15. Понятие случайной величины (СВ). Функция распределения случайной величины и её основные свойства.
16. Дискретная случайная величина (ДСВ). Ряд распределения, многоугольник распределения, функция распределения ДСВ, их построение.
17. Непрерывная случайная величина (НСВ). Функция плотности распределения и её основные свойства. Представление функции распределения НСВ через функцию плотности распределения.
18. Математическое ожидание дискретной и непрерывной случайной величин. Основные свойства математического ожидания.
19. Дисперсия и среднее квадратичное отклонение случайной величины. Основные свойства дисперсии. Вычисление дисперсии ДСВ и НСВ.
20. Мода. Квантиль и критическая точка, взаимосвязь между ними. Медиана.
21. Начальные и центральные моменты 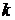 -ого порядка, взаимосвязь между ними. Вычисление моментов для ДСВ и НСВ. Асимметрия и эксцесс.
-ого порядка, взаимосвязь между ними. Вычисление моментов для ДСВ и НСВ. Асимметрия и эксцесс.
22. Биномиальный закон распределения ДСВ, его числовые характеристики (математическое ожидание и дисперсия), значение для практики.
23. Закон Пуассона распределения ДСВ, его числовые характеристики (математическое ожидание и дисперсия), значение для практики.
24. Поток событий, его свойства. Простейший (пуассоновский) поток событий.
25. Геометрический закон распределения ДСВ, его числовые характеристики (математическое ожидание и дисперсия), значение для практики.
26. Равномерный закон распределения НСВ, его числовые характеристики (математическое ожидание и дисперсия), значение для практики.
27. Показательный закон распределения НСВ, его числовые характеристики (математическое ожидание и дисперсия), значение для практики.
28. Нормальный закон распределения НСВ, его числовые характеристики (математическое ожидание, дисперсия, асимметрия, эксцесс). Особая роль нормального закона распределения.
29. Стандартный нормальный закон распределения. Интеграл Лапласа и его применение для вычисления вероятности попадания нормально распределённой случайной величины в заданный интервал. Правило «трёх сигм».
30. Понятие  -мерной случайной величины. Двумерная случайная величина. Функция распределения двумерной СВ, её основные свойства.
-мерной случайной величины. Двумерная случайная величина. Функция распределения двумерной СВ, её основные свойства.
31. Двумерная ДСВ, законы её распределения. Одномерные законы распределения составляющих, их математическое ожидание и дисперсия. Зависимость и независимость двух дискретных случайных величин.
32. Двумерная НСВ, законы её распределения. Одномерные законы распределения составляющих, их математическое ожидание и дисперсия. Зависимость и независимость двух непрерывных случайных величин.
33. Ковариация случайных величин. Коэффициент корреляции случайных величин и его основные свойства.
34. Условные законы распределения составляющих двумерной случайной величины. Условные математические ожидания. Функция и линия регрессии.
35. Двумерный нормальный закон распределения. Эллипс рассеяния.
36. Функция одного случайного аргумента. Нахождение закона распределения вероятностей функции от ДСВ и НСВ. Вычисление математического ожидания и дисперсии функции одного случайного аргумента.
37. Функция двух случайных аргументов. Закон распределения суммы независимых случайных величин. Формула свёртки.
38. Законы распределения случайных величин, представляющих функции нормальных величин: «хи-квадрат», Стьюдента, Фишера.
39. Сходимость последовательности случайных величин, её основные типы. Статистическая устойчивость среднего арифметического случайных величин.
40. Неравенства Чебышева, их значение для практики.
41. Закон больших чисел в форме Чебышева, его значение для практики.
42. Закон больших чисел в форме Бернулли, его значение для практики.
43. Центральная предельная теорема ТВ, её значение для практики. Интегральная теорема Муавра-Лапласа, как следствие центральной предельной теоремы ТВ.
Экзаменационные примеры.
1. Доказать свойство дисперсии: 
2. Доказать свойство дисперсии: Если  и
и  независимы, то
независимы, то 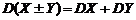 .
.
3. Распределение дискретной случайной величины  определяется формулой:
определяется формулой: 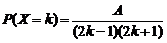 ,
,  . Найти постоянную
. Найти постоянную  и вероятность
и вероятность 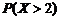 .
.
4. Доказать, что: коэффициент корреляции  не изменяется при линейных преобразованиях случайных величин
не изменяется при линейных преобразованиях случайных величин  и
и  с положительным коэффициентом растяжения, т.е.
с положительным коэффициентом растяжения, т.е. 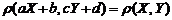 , где
, где 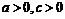 .
.
5. Известно, что совместное наступление событий  и
и  влечёт наступление события
влечёт наступление события  . Доказать, используя свойства вероятности, что
. Доказать, используя свойства вероятности, что  .
.
6. События  и
и  таковы, что
таковы, что  ,
, 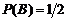 ,
,  . Найти, используя свойства вероятности, вероятности:
. Найти, используя свойства вероятности, вероятности:  и
и  .
.
7. Доказать, что центральный момент третьего порядка  случайной величины
случайной величины  связан с её начальными моментами первого, второго, третьего порядков:
связан с её начальными моментами первого, второго, третьего порядков:  равенством:
равенством:  .
.
8. Используя свойства вероятности, найти вероятности указанных событий:
а) вероятность 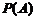 , если известны вероятности
, если известны вероятности  ,
,  =0.18.
=0.18.
б) вероятности 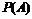 ,
,  ,
,  , если известно, что
, если известно, что  ,
,  ,
,  .
.
в) вероятность  , если известны вероятности
, если известны вероятности 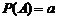 ,
,  ,
, 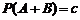 .
.
9. Дискретная случайная величина  имеет распределение Пуассона
имеет распределение Пуассона 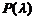 :
: 
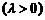 ,
,  . Доказать, что:
. Доказать, что:  .
.
10. Непрерывная случайная величина  имеет равномерное распределение
имеет равномерное распределение  :
: 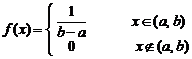 . Доказать, что
. Доказать, что 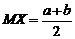 ,
, 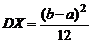 .
.
11. Непрерывная случайная величина  имеет показательное распределение
имеет показательное распределение  :
: 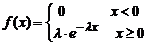
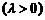 . Доказать, что
. Доказать, что 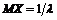 .
.
12. Пусть  и
и  - произвольные случайные величины. Доказать, что:
- произвольные случайные величины. Доказать, что:
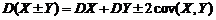 , где
, где  -ковариация величин
-ковариация величин  и
и  .
.
13.  ~
~ 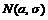 . Доказать, что линейная функция
. Доказать, что линейная функция  также имеет нормальный закон распределения, причём
также имеет нормальный закон распределения, причём 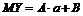 ,
,  .
.
14. Доказать, что из независимости событий  и
и  следует независимость событий
следует независимость событий 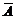 и
и 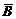 . (Указание: учесть, что
. (Указание: учесть, что  ).
).
Дополнительная литература.
1. Печинкин А.В., Тескин О.И., Цветкова Г.М. и др. Теория вероятностей. Учеб. для вузов. –М.:Изд-во МГТУ им.Н.Э.Баумана, 2004. -456с.
2. Кремер Н.Ш. Теория вероятностей и математическая статистика. Учебник для вузов. М.: ЮНИТИ-ДАНА, 2000.