Сложение ускорений при поступательном переносном движении.

Лекция 5

Краткое содержание: Скорости и ускорения точек тела при вращении. Векторные формулы для скоростей и ускорений точек тела. Сложное движение точки. Абсолютное, относительное и переносное движение точки. Сложение скоростей. Сложение ускорений при поступательном движении твердого тела.

 

Скорости и ускорения точек тела при вращении.

Перейдем к изучению движения отдельных точек твердого тела. Известно уравнение вращения твердого тела вокруг неподвижной оси .

Рассмотрим какою-нибудь точку М твердого тела, находящуюся на расстоянии h от оси вращения. При вращении твердого тела точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр О лежит на самой оси. Если за время происходит элементарный поворот тела на угол , то точка М при этом совершает вдоль своей траектории элементарное перемещение .

Тогда алгебраическая скорость будет равна

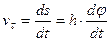или (5-1)

 

Рис. 5-1

Скорость точки равна 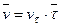. Скорость в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью.

Модуль скорости равен

. (5-2)

Величины скоростей точек тела, при его вращении вокруг неподвижной оси, пропорциональны кратчайшим расстояниям от этих точек до оси. Коэффициентом пропорциональности является угловая скорость . Скорости точек направлены по касательным к траекториям и, следовательно, перпендикулярны радиусам вращения.

Ускорение точки раскладывается на касательн ую и нормальную составляющие, т.е.

.

Касательное и нормальное ускорения вычисляются по формулам

, .

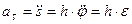Таким образом , и модуль ускорения вычисляется по формуле .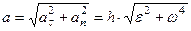

Касательные, нормальные и полные ускорения точек тела, при его вращении вокруг неподвижной оси, как и скорости, так же пропорциональны кратчайшим расстояниям от этих точек до оси. Нормальное ускорение направлено по радиусу окружности к оси вращения. Направление касательного ускорения зависит от знака углового ускорения.

Векторные скорости и ускорения точек тела

Скорость точки по модулю и направлению можно представить векторным произведением

, (5-3)

где - радиус-вектор точки М, проведенный из произвольной точки оси вращения .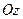

Это выражение называется векторной формулой Эйлера.

Доказательство. Вектор перпендикулярен плоскости, в которой расположены векторы 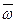и , следовательно, по направлению он совпадает со скоростью . Модуль векторного произведения Таким образом, векторное произведение по модулю и направлению определяет скорость точки.

 

Рис. 5-2

Определим ускорение точки продифференцировав формулу Эйлера.

, или

Первое слагаемое является касательным ускорением, а второе – нормальным.

.

Сопоставление двух формул для скорости точки ( и ) дает формулу для вычисления производной по времени от вектора :

.

В этой формуле вектор имеет постоянный модуль, так как соединяет все время две точки твердого тела.

 

 

Сложное движение точки

Основные понятия

Во многих задачах движение точки приходится рассматривать относительно двух (и более) систем отсчета, движущихся друг относительно друга.

В простейшем случае сложное движение точки состоит из относительного и переносного движений. Определим эти движения.

Рассмотрим две системы отсчета движущиеся друг относительно друга. Одну систему отсчета O ₁ x ₁ y ₁ z ₁ примем за основную и неподвижную. Вторая система отсчета Oxyz будет двигаться относительно первой.

Движение точки относительно подвижной системы отсчета Oxyz называется относительным. Характеристики этого движения, такие как, траектория, скорость и ускорение, называются относительными. Их обозначают индексом r.

Движение точки относительно основной неподвижной системы отсчета O ₁ x ₁ y ₁ z ₁называется абсолютным (или сложным). Траектория, скорость и ускорение этого движения называются абсолютными. Их обозначают без индекса.

Переносным движением точки называется движение, которое она совершает вместе с подвижной системой отсчета, как точка, жестко скрепленная с этой системой в рассматриваемый момент времени. Вследствие относительного движения движущаяся точка в различные моменты времени совпадает с различными точками тела S, с которым скреплена подвижная система отсчета. Переносной скоростью и переносным ускорением являются скорость и ускорение той точки тела S, с которой в данный момент совпадает движущаяся точка. Переносные скорость и ускорение обозначают индексом e.

Если траектории всех точек тела S, скрепленного с подвижной системой отсчета, изобразить на рисунке, то получим семейство линий – семейство траекторий переносного движения точки М. Вследствие относительного движения точки М в каждый момент времени она находится на одной из траекторий переносного движения.

Одно и то же абсолютное движение, выбирая различные подвижные системы отсчета, можно считать состоящим из разных переносных и соответственно относительных движений.

Пример.

Имеется круглый диск, который вращается с постоянной угловой скоростью вокруг оси перпендикулярной плоскости диска. На диске имеется канавка, направленная вдоль радиуса диска. Вдоль канавки перемещается материальная точка. Материальная точка совершает сложное движение. Движение точки относительно неподвижной системы отсчета является абсолютным. Подвижную систему отсчета жестко свяжем с вращающимся диском, одну из осей (например, x) направим вдоль канавки. Движение точки вдоль оси x будет относительным, движение точки вместе с подвижной системой отсчета (вместе с диском) будет переносным движением.

 

Сложение скоростей

Определим скорость абсолютного движения точки М, если известны скорости абсолютного и переносного движений этой точки.

За малый промежуток времени вдоль траектории точка М совершит относительное перемещение, определяемое вектором . Сама кривая , двигаясь вместе с подвижными осями, перейдет за тот же промежуток времени в новое положение Одновременно та точка кривой , с которой совпадала точка М, совершит переносное перемещение . В результате точка совершит перемещение .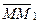

Деля обе части равенства на и переходя к пределу, получим

 

Сложение ускорений при поступательном переносном движении.

Определим ускорение абсолютного движения точки в частном случае поступательного переносного движения.

Справедлива теорема . Если подвижная система отсчета движется поступательно относительно неподвижной , то все точки тела, скрепленного с этой системой, имеют одинаковые скорости и ускорения, равные скорости и ускорению начала координат подвижной системы О. Следовательно, для скорости и ускорения переносного движения имеем

,

Выразим относительную скорость в декартовых координатах

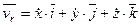
Подставляя в теорему о сложении скоростей значения переносной и относительной скоростей получаем

По определению

, , .

Следовательно,

Абсолютное ускорение точки при поступательном переносном движении равно векторной сумме ускорений переносного и относительного движений.