Приведём другое решение.

Алгебраические выражения

Критерии оце­ни­ва­ния вы­пол­не­ния задания	Баллы
Пре­об­ра­зо­ва­ния вы­пол­не­ны верно, по­лу­чен вер­ный ответ.
Ре­ше­ние до­ве­де­но до конца, но до­пу­ще­на ошиб­ка или опис­ка вы­чис­ли­тель­но­го характера, с её учётом даль­ней­шие шаги вы­пол­не­ны верно.
Дру­гие случаи, не со­от­вет­ству­ю­щие ука­зан­ным критериям.
Максимальный балл

1. Сократите дробь .

Решение.

Используем свой­ства степеней:

 

 

Ответ: 96.

Критерии проверки:

Источник: Демонстрационная вер­сия ГИА—2013 по математике.

Задание 21 № 311236

2. Разложите на множители: .

Решение.

Имеем:

 

Ответ: .

Критерии проверки:

 

*Ошибка в зна­ках при груп­пи­ров­ке сла­га­е­мых счи­та­ет­ся существенной, при ее на­ли­чии ре­ше­ние не засчитывается.

Задание 21 № 311243

3. Сократите дробь

Решение.

Корни квад­рат­но­го трехчлена

 

Имеем:

 

Замечание. Уча­щий­ся может раз­ло­жить трехчлен на мно­жи­те­ли каким-либо иным способом. Например:

 

Ответ:

Критерии проверки:

Задание 21 № 311255

4. Упростите вы­ра­же­ние

Решение.

Имеем:

 

Ответ:

Критерии проверки:

Источник: ГИА-2013. Математика. Диагностическая работа № 1. (вар. 1) 02.10.2012г.

Задание 21 № 311552

5. Один из кор­ней урав­не­ния равен 1. Най­ди­те вто­рой корень.

Решение.

Представим уравнение в виде: По теореме Виета откуда второй корень

 

Ответ: −0,6.

Критерии проверки:

Источник: ГИА-2013. Математика. Диагностическая работа № 1. (вар. 2) 02.10.12г.

Задание 21 № 311575

6. Упростите выражение: .

Решение.

Имеем:

 

Ответ: 2,4.

Критерии проверки:

Источник: ГИА-2013. Математика. Тренировочная работа № 1 (1 вар.)

Задание 21 № 311579

7. Упростите выражение: .

Решение.

Имеем:

.

 

Ответ: 4.

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Правильно вы­пол­не­ны преобразования, по­лу­чен верный ответ
Решение до­ве­де­но до конца, но до­пу­ще­на ошибка или опис­ка вычислительного характера, с её учётом даль­ней­шие шаги вы­пол­не­ны верно
Другие случаи, не со­от­вет­ству­ю­щие указанным выше критериям
Максимальный балл

Источник: ГИА-2013. Математика. Тренировочная работа № 1(2 вар)

Задание 21 № 311582

8. Упростите выражение: .

Решение.

1) .

2) .

Ответ: −3.

Критерии проверки:

Источник: ГИА-2013. Математика. Тренировочная работа № 2.(1 вар)

Задание 21 № 311584

9. Упростите выражение:

Решение.

Корни квад­рат­но­го трёхчлена
Значит,

 

 

 

Ответ:

Критерии проверки:

Источник: ГИА-2013. Математика. Тренировочная работа № 4.(1 вар.)

Задание 21 № 311588

10. Найдите зна­че­ние выражения: при

Решение.

Имеем:

 

При получаем:

Ответ:

Критерии проверки:

Источник: ГИА-2012. Математика. Диагностическая работа № 1(2 вар)

Задание 21 № 311592

11. Сократите дробь:

Решение.

Имеем:

 

Ответ: 2.

Критерии проверки:

Источник: ГИА-2012. Математика. Диагностическая работа № 2(1вар)

Задание 21 № 311599

12. Какое из чисел больше: или ?

Решение.

Найдем квад­ра­ты чисел:

;

 

 

.

 

Так как , то .
Учитывая, что и — положительные числа, получаем, что

.

 

Ответ: .

Критерии проверки:

Источник: ГИА-2013. Математика. Тренировочная работа № 4.(1 вар.)

Задание 21 № 311654

13. Сократите дробь , если .

Решение.

Имеем:

 

 

Ответ: 1.

Критерии проверки:

Источник: ГИА-2012. Математика. Диагностическая работа № 1 (3вар)

Задание 21 № 311921

14. Упростите вы­ра­же­ние

Решение.

 

Ответ:

Критерии проверки:

Источник: МИОО: Тре­ни­ро­воч­ная работа по ма­те­ма­ти­ке 19.11.2013 ва­ри­ант МА90201.

Задание 21 № 311965

15. Сократите дробь

Решение.

 

 

Ответ: 126.

Критерии проверки:

Источник: МИОО: Тре­ни­ро­воч­ная работа по ма­те­ма­ти­ке 19.11.2013 ва­ри­ант МА90202.

Задание 21 № 314310

16. Со­кра­ти­те дробь

Решение.

Последовательно раз­де­лим мно­го­член на од­но­чле­ны в столбик:

 

 

Ответ:

 

Приведём другое решение.

Разложим числитель на множители, используя метод группировки:

 

 

Критерии проверки:

Источник: Банк заданий ФИПИ

Задание 21 № 314410

17. Со­кра­ти­те дробь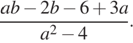

 

Решение.

Имеем:

 

Ответ:

Критерии проверки:

Источник: Банк заданий ФИПИ

Задание 21 № 318547

18. Найдите зна­че­ние вы­ра­же­ния при В от­ве­те за­пи­ши­те най­ден­ное зна­че­ние.

Решение.

Приведём дроби к об­ще­му знаменателю:

 

 

Таким образом, вы­ра­же­ние не за­ви­сит от зна­че­ний переменных, по­это­му оно равно -7.

 

Ответ: −7.

Критерии проверки:

Ответ: -7

-7

Задание 21 № 338112

19. Найдите зна­че­ние выражения если

Решение.

Преобразуем ра­вен­ство так, чтобы оно со­дер­жа­ло выражение

 

 

Ответ: 1.

Критерии проверки:

Источник: Банк заданий ФИПИ

Задание 21 № 338134

20. Найдите зна­че­ние вы­ра­же­ния если

Решение.

Найдём зна­че­ние выражения:

 

 

Ответ: −1.

Критерии проверки:

Ответ: -1

-1

Задание 21 № 338222

21. Найдите зна­че­ние вы­ра­же­ния если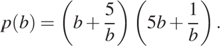

Решение.

Найдём зна­че­ние вы­ра­же­ния

 

Поэтому

Ответ: 1.

Критерии проверки:

Ответ: 1

Задание 21 № 340876

22. Найдите зна­че­ние вы­ра­же­ния 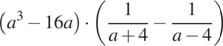при

Решение.

При a ≠ 4 и a ≠ −4 ис­ход­ное вы­ра­же­ние при­ни­ма­ет вид:

 

 

При a = −45 зна­че­ние этого вы­ра­же­ния равно 360.

 

Ответ: 360.

Критерии проверки:

Источник: СтатГрад: Тре­ни­ро­воч­ная ра­бо­та по ма­те­ма­ти­ке 26.11.2014 ва­ри­ант МА90202.

Задание 21 № 340931

23. Сократите дробь

Решение.

Преобразуем выражение:

 

 

Ответ: 80.

Критерии проверки:

Источник: СтатГрад: Тре­ни­ро­воч­ная ра­бо­та по ма­те­ма­ти­ке 26.11.2014 ва­ри­ант МА90204.

Задание 21 № 352715

24. Сократите дробь

Решение.

Упростим выражение:

 

 

Ответ: 0,8

Ответ: 0,8

0,8

Задание 21 № 353431

25. Найдите зна­че­ние вы­ра­же­ния если