Система оценивания результатов

1. Количество балов за каждую задачу теоретического тура лежит в пределах от 0 до 10.

2. Количество баллов за каждую задачу экспериментального тура может лежать в пределах от 0 до 10 баллов в 9 классах и от 0 до 15 баллов в 10 и 11 классах.

3. Если задача решена частично, то оценке подлежат этапы решения задачи. Не рекомендуется вводить дробные баллы. В крайнем случае, следует их округлять «в пользу ученика» до целых баллов.

4. Не допускается снятие баллов за «плохой почерк» или за решение задачи способом, не совпадающим со способом, предложенным методической комиссией.

Примечание. Вообще не следует слишком догматично следовать авторской системе оценивания (это лишь рекомендации!). Решения и подходы школьников могут отличаться от авторских, быть не рациональными.

Пример соответствия выставляемых баллов и решения, приведенного участником олимпиады.

Баллы	Правильность (ошибочность) решения
	Полное верное решение
	Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.
5-6	Решение в целом верное, однако содержит существенные ошибки (не физические, а математические).
	Найдено решение одного из двух возможных случаев.
2-3	Есть понимание физики явления, но не найдено одно из необходимых для решения уравнений, в результате полученная система уравнений не полна и невозможно найти решение.
0-1	Есть отдельные уравнения, относящиеся к сути задачи при отсутствии решения (или при ошибочном решении).
	Решение неверное, или отсутствует.

 

 

9 класс

 

Условия задач

 

 

Задача 1

Вес куска стекла в воде 1,5 Н. Определить его массу. Плотность стекла 2 500 кг/м³.

Задача 2

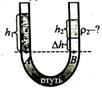
В U-образный сосуд налили ртуть, поверх нее в одно из колен налили столб масла высотой 48 см, а в другой - неизвестный раствор высотой 20 см. Разность уровней ртути в коленах сосуда 2 см. Определить плотность неизвестного раствора, если плотность ртути 13 600 кг/м³, а масла 900 кг/м³.

 

Задача 3

Два автомобиля имеют одинаковую мощность. Максимальная скорость первого 120 км/ч, а второго 130 км/ч. Какую максимальную скорость могут развить автомобили, если один возьмет на буксир другого, у которого двигатель отключен?

 

Задача 4

Определить плотность раствора медного купороса. Приборы и материалы:

1) два одинаковых стеклянных стаканчика;

2) раствор медного купороса;

3) вода;

4) измерительная линейка;

5) карандаш.

Решения задач

 

Задача 1.

 

F_apx =P₁- P₂, где Р₁ - вес в воздухе; Р₂ - вес стекла в воде.

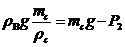
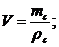F_apx =ρ_BgV;

 

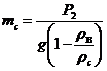Отсюда определяем т_c

Ответ: 250 г.

 

 

Задача 2.

Жидкости в сосуде находятся в равновесии, поэтому давление в точках А и В одинаково:

P_A=P_B; P_A=ρ₁gh₁; P_B=ρ₂ gh₂ + ρ_P·g r h

Приравнивая и преобразуя, окончательно получим:

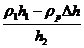
Ответ: 800 кг/м3.

 

Задача 3.

Пусть мощность каждого автомобиля Р. Тогда P = F_conp1 n₁

Р = F_conp2. × n₂ Когда один берет на буксир другой, то тогда

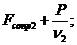
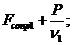P= (F_сопр1 + F_сопр2 )· n;

 

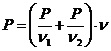
После преобразования окончательно получаем:

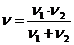
Ответ: 62,4 км/ч.

Задача 4.

 

1. Линейку положить на карандаш в положении равновесия
(равноплечный рычаг).

2. Стаканчики поставить на края линейки и, наливая в один во­ду, в другой - медного купороса, добиться равновесия.

3. Измерить линейкой высоту столбов воды (h ₁,) и медного ку­пороса (h ₂).

4. Применяя правило моментов сил, определяют плотность медного купороса:

M₁=M₂; F₁l₁=F₂l₂.

Так как 1₁=1₂ - плечи сил рычага, то m₁g=m₂g; m₁ = ρ₁V₁ =ρ_lSh_l; m₂ = ρ₂V₂ =ρ₂Sh₂; ρ_lSh_lg= ρ₂Sh₂g; ρ_lh₁= ρ₂h₂

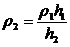
Отсюда

 

10 класс

 

Условия задач

Задача 1.

Пароход плывет по озеру со скоростью 36 км/ч. На палубе парохода спортсмен, играя в мяч, подбрасывает его вертикально вверх со скоростью 20 м/с, и мяч достигает высшей точки подъема. Каково перемещение мяча за это время относительно берега. Ускорение свободного падения 10 м/с².

Задача 2.

Два шара одинакового объема, но разной массы: 5 кг и 2 кг соединены нитью. Определить натяжение нити, соединяющей шары, если они плавают в вертикальном положении, полностью погрузившись в воду.

 

Задача 3.

К щепке, вмороженной в кусок льда объемом 0,001 м^З, привязана веревочка. Другой конец ее закреплен на дне сосуда с водой так, что весь лед погружен в воду. Определить, насколько изменится натяжение веревочки после того, как весь лед растает, а щепочка останется в воде. Плотность воды 1 000 кг/м^З, а плотность льда 900 кг/м³.

 

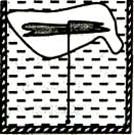
Задача 4.

С какой скоростью капля воды должна на лететь на такую же неподвижную каплю, чтобы в результате удара они испарились? Начальная температура капли 20°С, удельная теплоемкость воды 4 200 Дж/кг°С. Удельная теплота парообразования 2,3·10⁶Дж/кг.

Задача 5.

Определить удельную теплоту растворения поваренной соли.

Приборы и материалы:

1. весы;

2. разновес;

3. термометр;

4. калориметр;

5. стакан с водой;

6. поваренная соль.

 

 

Решение

 

Задача 1.

Высота подъема мяча относительно палубы , время движения мяча вверх .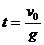

За это время пароход переместился относительно берега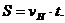

Тогда перемещение мяча относительно берега найдем по теоремеПифагора: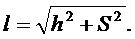

Ответ: 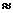28 м.

 

Задача 2.

Силы, действующие на нижний шарик: сила натяжения. Архимедова сила, сила тяжести:

F_и + F_арх =m₁g

Силы, действующие на верхний шарик: сила архимедова, сила тяжести, сила натяжения:

Fарх = F_и +m₂g

Решая систему двух уравнений, получаем:

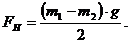
Ответ: 15 Н.

 

Задача 3.

1. Сила натяжения веревочки до таяния льда равна:

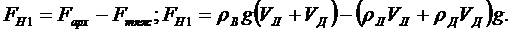
Когда лед растает: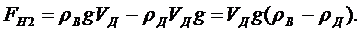
Окончательно получаем: F_H1 –F_H2 = gV_Л{p_в-p_Д)
Omвem: 1 Н.

Задача 4.

Из закона сохранения импульса: mv₀=2mv

Отсюда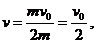

где v₀ - скорость падающей капли; v - скорость капель сразу после удара.

Из закона сохранения энергии:

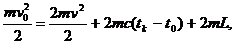(2)

где L - удельная теплота парообразования: t_K = 100°С.

При подстановке в (1) 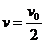и преобразований окончательно получаем:

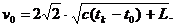
Ответ: 4,5 км/с.

 

Задача 5.

1. Определить массу соли с помощью весов (m).

2. По разности масс калориметра с водой и пустого калориметра определяем массу воды (т₀).

3. Термометром определяем начальную температуру воды в калориметре (t₀).

4. При опускании соли в воду и ее растворении температура во­ды понижается до (t).

5. Из уравнения теплового баланса находим удельную теплоту растворения соли:

где с — удельная теплоемкость воды.

 

11 класс

 

Условия задач

Задача 1.

Пловец прыгает с вышки с высоты h и погружается в воду на глубину 3,5 м за 0,5 с. Определите высоту вышки.

Дано: s = 3,5 м, t = 0,5 с.

Найти: h =?

 

Задача 2.

Сосуд разделен на три одинаковых отсека с теплоизолирую­щими перегородками, в которых сделаны небольшие отвер­стия. Температура газа вначале во всех отсеках была одинакова. Затем, поддерживая в первом отсеке прежнюю темпера­туру, во втором увеличиваем ее в 2 раза, а в третьем - в 3 раза. Определить, во сколько раз по сравнению с первоначальным увеличилось давление в сосуде.

 

Задача 3.

Определите, за какую часть периода отклоненный маят­ник проходит половину амплитуды.

Задача 4

Плоская горизонтальная фигура площадью S = 0,1 м², ограниченная проводящим контуром, находится в од­нородном магнитном поле. Пока проекция магнитной индукции на вертикаль Z равномерно меняется от

B_lz = 2 Тл до B_2z = -2 Тл, по контуру протекает заряд = 0,08 Кл. Найдите сопротивление контура.

 

 

Задача 5.

Определить показатель преломления стекла.

Приборы и материалы:

1) лист белой бумаги;

2) линейка;

3) стеклянная призма;

4) транспортир;

5) таблица синусов.

 

 

Решение

Задача 1.

Задача распадается на две части: движение в воде и движение в воздухе. Объединяет эти движения то, что конечная скорость движения в воздухе одновременно является начальной скоростью движения в воде.

Движение в воде. Определим, с какой скоростью пловец входит в воду (третий вариант формул равноускоренного движения):

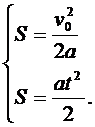
Перемножим равенства почленно:

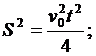
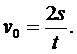
Движение в воздухе. Учитывая, что v = v₀, применяем формулу из пятого варианта:

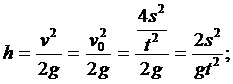
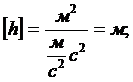
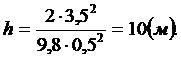
Ответ. h = 10 м.

Задача 2.

По закону Менделеева-Клапейрона вначале в сосуде было давление Р_о:

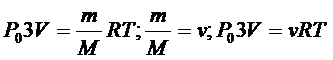
- в первом состоянии;

в конце:

PV=v_lRT - в I отсеке; PV=v₂R2T - во II отсеке;

PV = v₃R3T – в III отсеке.

Число молей газа:

Окончательно получаем:

Ответ: 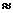1,6 раз.

Задача 3.

При гармонических колебаниях смещение определяется по формуле

х = х₀ cos ω t,

где х₀ - амплитуда, ω - циклическая частота, 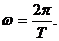По условию

Напомним, что координата х отсчитывается от положения равновесия, а не от крайнего положения. Поэтому, чтобы найти координату, нужно от амплитуды отнять пройденную часть. Подставляем смещение в формулу гармонических колебаний:

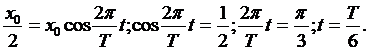
Ответ. За шестую часть периода.

 

 

Задача 4.

По закону электромагнитной индукции в случае однородного поля: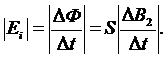

2) С другой стороны, так что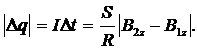

3) Отсюда 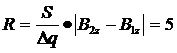Ом.

 

Задача 5.

1. На белом листе бумаги начертить с помощью линейки две параллельные прямые на расстоянии не более 1 см друг от друга.

2. На эти линии положить стеклянную призму.

3. Расположить глаз на уровне листа бумаги и поворачивать призму до смещения двух линий в одну, наблюдаемую сквозь
боковые грани стекла.

4. Осторожно очертить контур призмы и пометить точками (А)
входящую в призму линию и выходящую (В) из нее. Это бу­дет падающий и вышедший из призмы луч.

5. 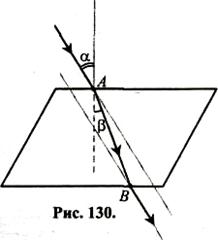Снять призму с бумаги и соединить конец падающего луча (А) с началом вышедшего из призмы луча (В). Получим преломленный
луч (АВ).

6. Восстановить перпендикуляр к грани призмы в точке падения луча А. Отметить угол падения αи угол преломления β.

7. Измерить транспортиром угол
падения (α) и угол преломления (β)луча.

8. 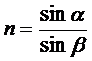Вычислить показатель преломления стекла п формуле закона
преломления света: