Ø Макроскопические параметры
Поведение макроскопических тел, в частности газов, можно охарактеризовать немногим числом физических величин, относящихся не к отдельным молекулам, слагающим тела, а ко всем молекулам в целом. К числу таких величин относятся объем V, давление р, температура 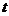 и др.
и др.
Так, газ данной массы всегда занимает некоторый объем, имеет определенные давление и температуру. Объем и давление представляют собой механические величины, описывающие состояние газа. Температура в механике не рассматривается, так как она характеризует внутреннее состояние тела.
Величины, характеризующие состояние макроскопических тел без учета молекулярного строения тел (V, р, t) называют макроскопическими параметрами.
Ø Температура и её существенные признаки
1) В обыденной жизни под температурой понимают степень нагретости тел.
2) Эта такая величина, которая обязательно одинакова для тел, находящихся в тепловом равновесии (это такое состояние, при котором все макроскопические параметры остаются неизменными сколь угодно времени при отсутствии внешних воздействий)
3) Температура – величина неаддитивная (температура системы 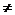 сумме температур её частей)
сумме температур её частей)
4) Температура есть величина, указывающая направление теплообмена (теплообмен происходит при разных температурах тел, находящихся в контакте. Теплота передается от более нагретому к менее нагретому)
Примечание. Если состояние какого – либо тела принять за нулевое, то температура есть величина, являющаяся мерой отклонения исследуемого тела, от состояния тела, принятого за нулевое.
Ø Средняя кинетическая энергия молекул газа при тепловом равновесии.
В состоянии теплового равновесия все газы имеют одинаковую температуру, не зависящую от рода газа. Для определения температуры выясним, какая физическая величина в молекулярно-кинетической теории обладает таким же свойством.
Из курса физики VII класса известно, что, чем быстрее движутся молекулы, тем выше температура тела. При нагревании газа в замкнутом сосуде давление газа возрастает. Согласно же основному уравнению молекулярно-кинетической теории (1.15) давление р прямо пропорционально средней кинетической энергии поступательного движения молекул. При тепловом равновесии, если давление газа данной массы и его объем фиксированы, средняя кинетическая энергия молекул газа должна иметь строго определенное значение, как и температура.
Так как концентрация молекул газа 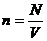 , то из уравнения
, то из уравнения 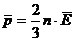 вытекает
вытекает
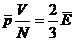
Давление и объем измеряются непосредственно. Число молекул можно определить, зная массу газа т, постоянную Авогадро 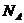 и молярную массу М.
и молярную массу М.
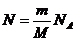
Если кинетическая энергия 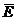 действительно одна и та же величина для всех газов в состоянии теплового равновесия, то и величина
действительно одна и та же величина для всех газов в состоянии теплового равновесия, то и величина 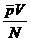 должна быть тоже одинаковой для всех газов.
должна быть тоже одинаковой для всех газов.
Ø Газы в состоянии теплового равновесия.
Опыт можно осуществить так. Возьмем несколько сосудов, заполненных различными газами, например водородом, гелием и кислородом. Сосуды имеют определенные объемы и снабжены манометрами. Это позволяет измерить давление в каждом сосуде. Массы газов известны, тем самым известно число молекул в каждом сосуде.
Приведем газы в состояние теплового равновесия. Для этого поместим их в тающий лед и подождем, пока не установится тепловое равновесие, и давление газов перестанет меняться (рис. 19). После того можно утверждать, что все газы имеют одинаковую температуру 0°С. Давления газов р, их объемы V и число молекул N различны. Измеряя все эти параметры получим:
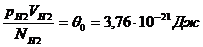
Такое же значение отношения произведения давления газа на его объем к числу молекул получается и для всех других газов при температуре тающего льда.
Если же сосуды с газами поместить в кипящую воду при нормальном атмосферном давлении,
то отношение 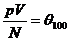 по-прежнему будет одним и тем же для всех газов, но больше, чем предыдущее. Как показывает опыт,
по-прежнему будет одним и тем же для всех газов, но больше, чем предыдущее. Как показывает опыт,
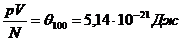
Ø Определение температуры.
Можно, следовательно, утверждать, что, величина 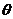 растет с повышением температуры. Более того,
растет с повышением температуры. Более того, 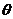 ни от чего, кроме температуры, не зависит. В принципе можно было бы считать температурой и саму величину
ни от чего, кроме температуры, не зависит. В принципе можно было бы считать температурой и саму величину 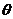 и измерять температуру в энергетических единицах — джоулях. Однако, во-первых, это неудобно для практического использования (100°С соответствовала бы очень малая величина — порядка
и измерять температуру в энергетических единицах — джоулях. Однако, во-первых, это неудобно для практического использования (100°С соответствовала бы очень малая величина — порядка 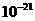 Дж), а во-вторых, и это главное, уже давно принято выражать температуру в градусах.
Дж), а во-вторых, и это главное, уже давно принято выражать температуру в градусах.
Будем считать величину 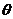 прямо пропорциональной температуре Т, измеряемой в градусах:
прямо пропорциональной температуре Т, измеряемой в градусах:
(2.5)
где k — коэффициент пропорциональности. Определенная равенством (2.5) температура называется абсолютной. Такое название, как мы сейчас увидим, имеет достаточные основания.
Учитывая определение (2.5), получим:
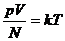 (2.6)
(2.6)
На основании этой формулы вводится температурная шкала (в градусах), не зависящая от вещества, используемого для измерения температуры.
Ø Абсолютный нуль температуры
Температура, определяемая формулой (2.6), очевидно, не может быть отрицательной, так как все величины, стоящие в левой части этой формулы заведомо положительны. Следовательно, возможным наименьшим значением температуры Т является Т = 0, если давление р или объем V равны нулю.
Предельную температуру, при которой давление идеального газа обращается в нуль при фиксированном объеме или объем идеального газа стремится к нулю при неизменном давлении, называют абсолютным нулем температуры.
Ø Абсолютная шкала температур.
Английский ученый У. Кельвин (1824—1907) ввел абсолютную шкалу температур. Нулевая температура по абсолютной шкале (ее называют также шкалой Кельвина) соответствует абсолютному нулю, а каждая единица температуры по этой шкале равна градусу по шкале Цельсия.
Единица абсолютной температуры в СИ называется Кельвином (обозначается буквой К).
Ø Постоянная Больцмана.
Определим коэффициент k в формуле (2.6) так, чтобы один кельвин (1 К) равнялся градусу по шкале Цельсия (1°С).
Мы знаем значения 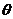 при О °С и 100 °С.
при О °С и 100 °С.
Обозначим абсолютную температуру при 0° С через 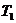 , а при 100 °С через
, а при 100 °С через 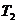 Тогда согласно (2.5)
Тогда согласно (2.5)
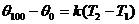
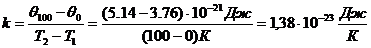
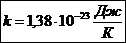
называется постоянной Больцмана в честь Л. Больцмана, одного из описателей молекулярно-кинетической теории газов. Постоянная Больцмана связывает температуру в энергетических единицах с температурой Т в кельвинах.
Ø Связь абсолютной шкалы и Шкалы Цельсия.
Зная постоянную Больцмана, можно найти значение абсолютного нуля по шкале Цельсия. Для этого найдем сначала значение абсолютной температуры, соответствующее 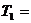 0°С.
0°С.
Так как при 0°С 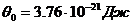 , а
, а 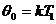 , то
, то
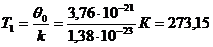 К
К
Поэтому любое значение абсолютной температуры Т будет на 273 градуса выше соответствующей температуры 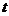 по Цельсию:
по Цельсию:
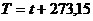
Но изменение абсолютной температуры 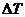 равно изменению температуры по шкале Цельсия
равно изменению температуры по шкале Цельсия 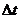 :
: 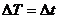 .
.
Ø Температура — мера средней кинетической энергии молекул.
Согласно основному уравнению МКТ:
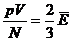
С другой стороны:
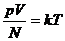
тогда
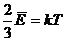
или
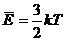
Средняя кинетическая энергия хаотического поступательного движения молекул газа пропорциональна абсолютной температуре.
Ø Третий вид основного уравнения МКТ
подставляя 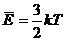 в
в 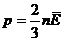 получим:
получим:
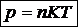
Ø Средняя скорость теплового движения молекул
Из механики известно, что
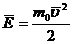
С другой стороны
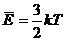
Тогда
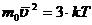
или
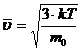
где 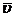 - средняя квадратичная скорость.
- средняя квадратичная скорость.
Ø Измерение температуры. Термометры.
Для измерения температуры можно воспользоваться изменением любой макроскопической величины в зависимости от температуры: объема, давления, электрического сопротивления и т. д.
Чаще всего на практике используют зависимость объема жидкости (ртути или спирта) от температуры. При градуировке термометра обычно за начало отсчета (0) принимают температуру тающего льда; второй постоянной точкой (100) считают температуру кипения воды при нормальном атмосферном давлении (шкала Цельсия). Шкалу между точками 0 и 100 делят на 100 равных частей, называемых градусами (рис, 140). Перемещение столбика жидкости на одно деление соответствует изменению температуры на 1 °С.
Так как различные жидкости расширяются при нагревании неодинаково, то установленная таким образом шкала будет до некоторой степени зависеть от свойств данной жидкости. Конечно, 0 и 100 °С будут совпадать у всех термометров, но, скажем, 50 °С совпадать не будут.
Какое же вещество выбрать для того, чтобы избавиться от этой зависимости? Было замечено, что в отличие от жидкостей все разреженные газы — водород, гелий, кислород — расширяются при нагревании одинаково и одинаково меняют свое давление при изменении температуры. По этой причине в физике для установления рациональной температурной шкалы используют изменение давления определенного количества разреженного газа при постоянном объеме или изменение объема газа при постоянном давлении. Такую шкалу иногда называют идеальной газовой шкалой температур. При ее установлении удается избавиться еще от одного существенного недостатка шкалы Цельсия — произвольности выбора начала отсчета, т. е. нулевой температуры. Ведь за начало отсчета вместо температуры таяния льда с тем же успехом можно было бы взять температуру кипения воды.