Лабораторная работа №4
Модулированные колебания
1. Цель работы: исследование радиосигналов с амплитудной и частотной модуляцией. Установление связей между временными и спектральными характеристиками радиосигналов.
Теоретические основы
Высокочастотные колебания легко генерируются, излучаются, хорошо распространяются в окружающей среде и принимаются приемными антеннами. Чтобы высокочастотный сигнал мог переносить информацию, производят модуляцию сигнала информационным сообщением. Для этого управляют либо амплитудой, либо фазой, либо частотой передаваемого сигнала в соответствии с передаваемой информацией. Широко распространенными являются радиосигналы с амплитудной, фазовой или частотной модуляцией. Модуляцию сигнала по частоте или фазе обобщенно называют угловой модуляцией.
Амплитудная модуляция
С качественной стороны амплитудная модуляция (AM) может быть определена как изменение амплитуды несущей пропорционально амплитуде модулирующего сигнала (рис. 2.1).
Рис. 2.1 Амплитудно-модулированный сигнал
Аналитически амплитудно-модулированное (АМ) колебание можно записать
,
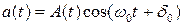где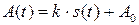 
, s(t) – модулирующий (управляющий) сигнал, 
- несущая, k – коэффициент пропорциональности.
Уравнение (1) представляет собой сигнал, состоящий из двух колебаний с частотами 
и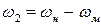 
и амплитудами АнАм/2. ω1 и ω 2 называются боковыми полосами, представляют собой две полосы частот — выше и ниже несущей (рис. 2.2), т. е. верхнюю и нижнюю боковую полосу соответственно. Вся информация, которую необходимо передать, содержится в этих боковых полосах частот.
(1)
Амплитуда модулированной несущей будет изменяться от нуля (
) до АнАм (
). Член [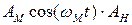 
] является амплитудой модулированных колебаний и прямо зависит от мгновенного значения модулирующей синусоиды.
Отношение m= Ам/Ан определяет коэффициент модуляции. Амплитуда модулированной волны изменяется от нуля до удвоенного значения амплитуды несущей. Для предотвращения искажений передаваемой информации — модулированного сигнала — значение m должно быть в пределах от нуля до единицы. На рис. 2.1 коэффициент модуляции m выражен через максимальное и минимальное значения ее амплитуды (пикового и узлового значений).
Глубина амплитудной модуляции - максимальное относительное отклонение амплитуды от среднего:
Рис. 2.2 дает представление о спектре модулированных колебаний, который может быть выражен преобразованием уравнения (1):
Рис. 2.2 Спектр амплитудно-модулированного сигнала
Спектральная плотность модулированного сигнала (рис 2.3) представляет два спектра модулирующей функции, построенных относительно частот 
и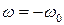 
(сдвинутых на частоты несущей).
Рис 2.3 Спектральная плотность модулированного сигнала
- свертка.
- спектральная плотность функции А(t).
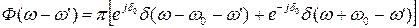- спектр несущей.
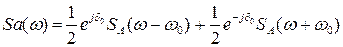
Частотная модуляция 
В методе частотной модуляции (ЧМ) амплитуда модулирующего сигнала управляет мгновенной частотой несущей. Идеальная ЧМ не вносит изменений в амплитуду несущей (рис. 2.4).
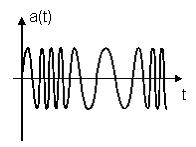
Рис. 2.4 Частотно-модулированный сигнал
ЧМ - колебание: 
; 
.
Фазовая модуляция: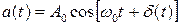 
; 
.
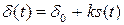Между частотой и фазовой модуляцией существует связь: 
, поэтому их часто объединяют в угловую модуляцию 
.
Девиация частоты - максимальное отклонение частоты как при частотной, так и при фазовой модуляции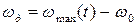 
.
При частотной модуляции: 
;
При фазовой модуляции: 
.
Индекс угловой модуляции - максимальное изменение фазы:
При частотной модуляции 
.
При фазовой модуляции: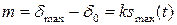 
.
Для неискаженной передачи сообщения необходимо, чтобы ширина спектра сообщения была мала по сравнению с несущей ω0, а для этого необходимо, чтобы относительное изменение модулирующей функции A(t), ω (t), δ(t) были малы за один период несущего колебания.
; 
; 
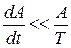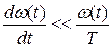Спектр радиосигнала при угловой модуляции
При фазовой модуляции: 
; при частотной 
.
Преобразуем косинус суммы: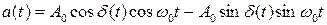 
и 
- медленно изменяющиеся амплитуды.
Итак, модулированное по углу колебание можно рассматривать как сумму двух амплитудно-модулированных колебаний (квадрупольных). Для определения спектра каждого из них достаточно сдвинуть на ω0 спектр огибающих амплитуд, т. к. cosδ(t) и sinδ(t) являются нелинейными функциями своего аргумента δ(t), то спектры этих функций могут существенно отличаться от спектра модулирующей функции s(t) и при однотональной модуляции возможно возникновение кратных и комбинированных частот.
Однако при малых индексах модуляции 
, 
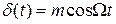можно положить 
; 
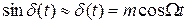, тогда
т. е. спектр, как и в случае амплитудной модуляции, состоит из несущей и двух боковых частей (но сдвинутых по фазе).
Рис. 2.5 Спектр частотно-модулированного сигнала, ω н - несущая частота; ω м - частота модуляции
При больших индексах модуляции за счет появления новых гармоник спектр расширяется и ширина спектра равна 2m ω, вместо 2ω при m << 1.
При m >1 cos(mcos ωt) и sin (mcos ωt) разлагают в ряд по Бесселевым функциям (рис. 2.6).
Рис. 2.6 Спектр частотно-модулированного сигнала при m > 1
Импульсно-модулированные сигналы (манипулированные сигналы)
В импульсной модуляции в качестве носителя управляющих сигналов используется последовательность прямоугольных импульсов. При радиосигналах эта последовательность наносится на высокочастотное колебание (двойная модуляция).
1) Амплитудно-импульсная модуляция (АИМ), когда по закону управляющего сигнала изменяется приращение амплитуды импульсов.
Рис. 2.7 Амплитудно-импульсная модуляция
, 
, 
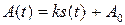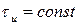2) Модуляция по длительности импульсов (ДИМ), когда по закону управляющего сигнала меняется длительность импульса. Иногда этот вид модуляции называется широтно-импульсной модуляцией(ШИМ).
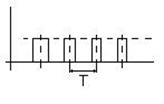
Рис. 2.8 Модуляция по длительности импульсов
, 
,
3) Временная импульсная модуляция (ВИМ), когда по закону управляющего сигнала происходит смещение импульсов по временной оси (может быть фазовой (ФИМ) или частотной (ЧИМ)).
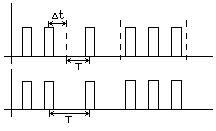
Рис. 2.9 Временная импульсная модуляция
ФИМ: 
, , ,
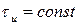ЧИМ: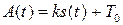 
, , .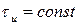