ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
На тему «Изучение свободных механических колебаний на примере математического и пружинного маятников»
Выполнил:
студент гр. Э-104
Зиборов Степан Сергеевич
Подпись _____________
Проверил:
преподаватель
Колосова Юлия Валентиновна,
Подпись ______________
Консультант (если есть):
Преподаватель
Богданова Светлана Борисовна,
Подпись ______________
Орел, 2021
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ. 3
РАЗДЕЛ I.Теория работы математического и пружинного маятника. 5
1.1 Основы колебаний в физике. 5
1.2 Теория математического маятника. 6
1.3 Теория пружинного маятника. 7
РАЗДЕЛ II. Изучение колебаний маятника. 9
2.1 Описание теоретической части. 9
2.2 Процесс изготовления маятника. 10
2.3 Изучение колебаний. 12
ЗАКЛЮЧЕНИЕ. 14
СПИСОК ИСТОЧНИКОВ.. 15
ВВЕДЕНИЕ
Тема проекта и её актуальность:
Я выбрал тему «Изучение свободных механических колебаний на примере математического и пружинного маятников» из-за того что я посмотрел документальный фильм «Рукотворные чудеса – Тайпей 101»(2006). В этом фильме при строительстве здания применили свойства маятника, что бы избежать разрушения здания во время землетрясений. Так же свойства маятника можно применить в строительстве мостов, для их баланса во время ветров.
Цель проекта:
Донести до зрителя доступным способом как происходят колебания маятника. Каким законам подчиняется данный физический процесс.
Задачи:
Изучить теорию
Понять как работает маятник
Донести информацию до зрителя простым и понятным языком
Создать действующую модель
На живом примере убедиться как происходят колебания
Этапы работы над проектом:
Определил направление работы
Выбрал тему проекта и разработал актуальность проекта
Проанализировал источники информации
Провёл исследования
Подготовил презентацию
Гипотеза -
Объект исследования – Маятник и его колебания
Предмет исследования – Физика
Метод (методика) и приёмы проведения исследования – Получение информации о предмете проекта из научной литературы и их практическое применение. Эксперимент
РАЗДЕЛ I. Теория работы математического и пружинного маятника.
Основы колебаний в физике
Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.
Существует три вида колебаний:
Свободные (или собственные) колебания – это колебания которые происходят под действием внутренних сил в колебательной системе.
Вынужденные колебания – это колебания, происходящие под воздействием внешних периодических сил.
Автоколебания – это колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний.
Основным признаком колебательного движения является его периодичность. Колеблющееся тело за одно колебание дважды проходит положение равновесия. Колебания характеризуются такими величинами как период, частота, амплитуда и фаза колебаний.
Разберём подробнее эти величины:
Период – это время одного полного колебания. Чтобы найти период колебаний нужно разделить время колебаний на число колебаний.
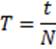
2. Частота колебаний – это число колебаний за единицу времени.
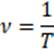
Амплитуда – это наибольшее смещение колеблющейся величины от положения равновесия.
Фаза колебаний – это физическая величина, которая показывает отклонение точки от положения равновесия.
φ =2πνt
Теория математического маятника
Математический маятник – это система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной L, на которой материальная точка подвешена, и которая находится в однородном поле сил тяготения.
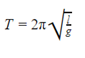
Один из видов движений математического маятника, называется движение по сепаратисе. Сепаратрисой называют траекторию динамической системы, у которой двумерное фазовое пространство. Если амплитуда колебаний маятника приближается к числу π, это говорит о том, что движение на фазовой плоскости приближается к сепаратрисе. Только тогда, когда математический маятник осуществляет малые колебания, он является гармоническим осциллятором. Иными словами, он становится механической системой, способной выполнять гармонические колебания. Такое приближение практически справедливо для углов в 15–20°. Колебания маятника с большими амплитудами не является гармоническим
Рассмотрим закон Ньютона для малых колебаний математического маятника. Если данная механическая система выполняет малые колебания, 2-й закон Ньютона будет выглядеть таким образом:
mg τ = Fτ = –m* g/L* x
Исходя из этого, можно заключить, что тангенциальное ускорение математического маятника пропорционально его смещению со знаком «минус». Это и является условием, благодаря которому система становится гармоническим осциллятором.
Так же существуют связанные маятники. Связанные маятники – это система где два математических маятника связанные пружиной.
Систему из двух связанных маятников можно рассматривать как две взаимодействующие между собой отдельные колебательные системы с одной степенью свободы.
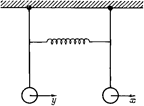
Связанные колебания маятников характеризуются константой связи, которая в этом случае записывается так:
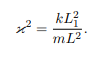
Этот коэффициент также имеет размерность квадрата частоты и зависит от параметров колебательной системы.