Вопрос №1
Идеальный газ. Законы идеальных газов
Идеальным называется газ, у которого объемы молекул бесконечно малы и отсутствуют силы межмолекулярного взаимодействия. Молекулы идеального газа представляют собой материальные точки, взаимодействие между которыми ограничено молекулярными соударениями.
Любой реальный газ тем ближе к идеальному, чем ниже его давление и выше температура. Например, окружающий нас воздух можно считать идеальным газом. Понятие идеального газа и законы идеальных газов полезны в качестве предела законов реального газа.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Закон Авогадро
Согласно этому закону, все газы при одинаковых температурах и одинаковом давлении содержат в одном и том же объеме одинаковое число молекул. Большую техническую значимость имеет следствие из закона Авогадро: объемы киломолей различных газов равны, если они находятся при одинаковых температурах и давлениях. При нормальных физических условиях (Т= 273,15 К, р = 760 мм рт. ст.) объем киломоля любого вещества равен Vµ=µν=22,4 м3/кмоль. Напомним, что киломолем называется количество вещества в килограммах, численно равное его молекулярной массе.
Закон Бойля — Мариотта
Этот закон был открыт независимо друг от друга английским физиком Р. Бойлем и французским ученым Э. Мариоттом. Ими было доказано, что при постоянной температуре газа произведение давления газа на его объем есть величина постоянная, т.е. при
Т = const
рV = const и рv = const.
Закон Гей-Люссака
Этот закон устанавливает, что если в процессе нагрева или охлаждения газа давление подцерживается постоянным, то объем изменяется пропорционально абсолютной температуре, т.е. если
Р = const, то и v/ Т = const.
Если же мы рассмотрим процесс нагрева или охлаждения газа в сосуде постоянного объема (v= const), то р/Т = const.
Уравнение состояния идеального газа
Для 1 кг газа Клапейроном установлено уравнение состояния рv = RT, в котором газовая постоянная Rимеет для каждого газа свое постоянное значение. Измеряется Rв Дж/кг-К и имеет вполне определенный физический смысл — это работа, совершаемая 1 кг газа при его нагреве на один кельвин при постоянном давлении. Для газа с произвольной массой M/(кг) уравнение состояния имеет вид
рV=МRТ.
Для одного киломоля вещества уравнение состояния (получено Д.И. Менделеевым) имеет вид рVµ =µRT, где µR— универсальная газовая постоянная, которая одинакова для всех газов и равна 8314 Дж/кмольК.
Во всех этих уравнениях давление подставляется в Па, температура — в К, объем — в м3 и удельный объем — в м3/кг.
Пример.
В резервуаре объемом 10 м3 находится азот при избыточном давлении 100 кПа и при температуре 27 °С. Атмосферное давление равно 750 мм рт. ст. Требуется найти массу и плотность азота.
Выразим атмосферное давление в паскалях: рб = 105 Па.
Абсолютное давление газа равно:p =ри +рб = 100 • 103 + 105 = = 2 • 105 Па.
Газовая постоянная азота равна (µ = 28 кг/кмоль)
R = 8314/28 = 297 Дж/кгЧК. Масса газа равна
М =рV/RT= 2*105* 10/297 • (273,15 + 27) = 22,43 кг.
Плотность азота
р = M /V= 22,43/10 = 2,243 кг/м3.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Свойства реальных газов
Свойства реальных газов значительно отличаются от свойств идеальных газов, причем отличия тем значительнее, чем выше давление и ниже температура газа. Это объясняется тем, что молекулы реальных газов имеют конечный объем и между ними существуют силы межмолекулярного взаимодействия. Уравнение состояния 1 кг реального газа имеет вид
рv = zRT,
где z= φ (р, T) — коэффициент сжимаемости, который может быть как больше, так и меньше единицы.
При проведении термодинамических расчетов с реальными газами нужно учитывать зависимость внутренней энергии, энтальпии и теплоемкости не только от температуры, но и от давления газа. При одном и том же давлении какое-либо вещество в зависимости от температуры может находиться в разных состояниях.
Из физики известно, что любое вещество может находиться в твердом, жидком или газообразном состоянии. Эти состояния будем называть фазами, а процесс перехода из одного состояния в другое — фазовым переходом.
При определенных условиях могут существовать одновременно две фазы вещества, например, лед и жидкость, пар и жидкость. Если пар и жидкость находятся в состоянии равновесия, то пар называется насыщенным.
У всех веществ фазовые переходы происходят при определенных физических параметрах, поэтому рассмотрение свойств реальных газов можно начать на примере вещества, которое является основным рабочим телом в циклах тепловых электростанций, в том числе и атомных. Этим рабочим телом является вода, и не только потому, что она относительно дешева и нетоксична, а потому, что она обладает благоприятными для работы термодинамическими свойствами.
Рассмотрим диаграмму «v—p » воды и водяного пара, на которой изобразим границы между фазами (рис. 1.1). В области а находится в равновесии смесь льда и некипящей воды, в области Ь находится некипящая вода, в области с находится смесь кипящей воды и водяного пара, в области d— перегретый водяной пар. Прямой 1-2 показан изобарный процесс подвода теплоты.
Показанные на рис. 1.1 кривые называются пограничными; кривые, ограничивающие с двух сторон область с, называются левой и правой пограничными кривыми. Им соответствуют кипящая вода (левой) и сухой насыщенный пар (правой). Область между этими кривыми называется областью влажного насыщенного пара — в этой области находятся в равновесии сухой насыщенный пар и кипящая вода. Смесь сухого насыщенного пара и кипящей воды называют влажным насыщенным паром. Масса влажного насыщенного пара равна
М = M'+ M ",
где М' — масса кипящей воды и М" — масса сухого насыщенного пара.
В дальнейшем все параметры, относящиеся к кипящей жидкости, будут иметь индекс «штрих» (р', h'и т.д.), а все параметры, относящиеся к сухому насыщенному пару,— индекс «два штриха» (р', h" и т.д.).
Температуру и давление насыщенного пара принято обозначать Тн и рн. В то же время в ряде литературных источников их обозначают Тs и рs (буква s является первой буквой английского слова s аturation — насыщение). Отношение массы сухого насыщенного пара к общей массе влажного насыщенного пара называется степенью сухости и обозначается х. Ясно, что на левой пограничной кривой х = 0, а на правой — х = 1. Разность {1-х) называется степенью влажности.
Чем выше давление пара, тем меньше расстояние по горизонтали между левой и правой пограничными кривыми, а при определенном давлении пара эти кривые смыкаются. Точка, в которой исчезают различия в свойствах кипящей жидкости и сухого насыщенного пара, называется критической (точка к на рис. 1.1).
Термические параметры различных веществ в критической точке различны. Эти параметры для ряда химических веществ приведены в табл. 1
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Таблица 1 Критические параметры веществ
| Вещество | Tкр, К | pкр,МПа | ρкр, кг/м3 |
| Азот N2 | 3,40 | ||
| Водород Н2 | 33,2 | 1,29 | |
| Водяной пар H2O | 647,12 | 22,115 | |
| Кислород О2 | 5,05 | ||
| Ртуть Нg | — | ||
| Диоксид углерода СО2 | 7,38 |
При сверхкритическом давлении не может быть влажного насыщенного пара. Если давление пара больше критического и постоянно по величине (р > ркр), то при подводе (или отводе) теплоты физические параметры (удельный объем, энтальпия и др.) меняются плавно, в то же время наблюдается резкое изменение тепло-емкостей сp исvв тех процессах, где сверхперегретая вода переходит в сверхперегретый водяной пар.
Уравнения состояния реальных газов
Известно значительное число уравнений состояния реальных газов, и одна из самых удачных попыток была сделана Ван-дер-Ваальсом, который получил уравнение в виде
(p + a/v2)(v-b)=RT (1)
Слагаемое a/v2 учитывает внутреннее давление, обусловленное силами взаимодействия молекул газа, а величина b— уменьшение объема, в котором движутся молекулы реального газа. Если по этому уравнению находить величины удельных объемов реальных газов, то уравнение (1) имеет три действительных корня при Т< Ткр и один действительный и два комплексных корня при Т > Ткр. Точность вычислений по этому уравнению невелика.
В самой общей форме уравнение состояния реальных газов имеет вид
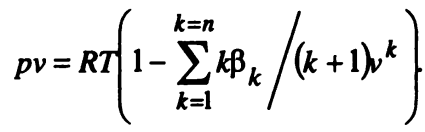 (2)
(2)
где 𝛽k — вириальные коэффициенты, зависящие от температуры газа.
Число членов ряда в уравнении (2) может быть достаточно велико, поэтому расчеты по этому уравнению вызывают значительные трудности.
Вопрос №14
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
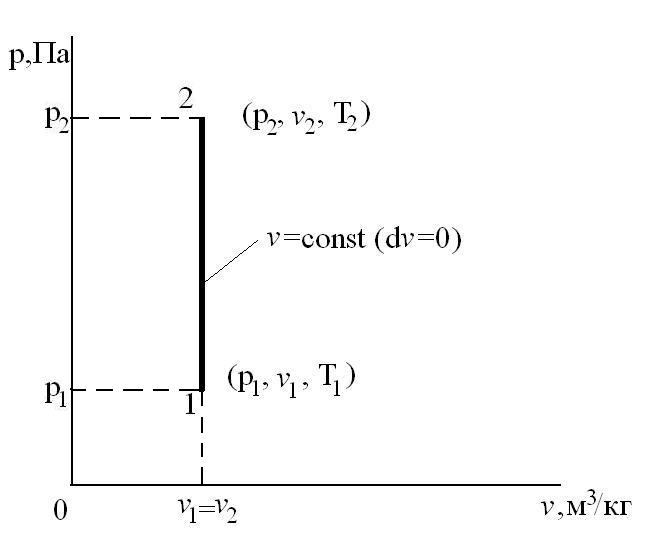
Этот процесс используется как подготовительный процесс в циклах.
Соотношение между параметрами для конечного участка процесса 1-2 определяется законом Шарля: 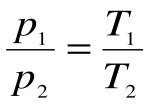 , который следует из уравнений состояния для точек 1 и 2:
, который следует из уравнений состояния для точек 1 и 2:
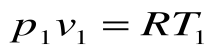 и
и 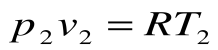 при
при 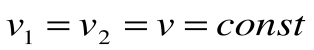 .
.
Поскольку работа расширения в этом процессе равна нулю: 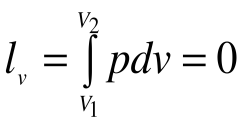 , т.к.
, т.к. 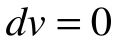 , то из уравнения 1-го закона термодинамики следует, что:
, то из уравнения 1-го закона термодинамики следует, что:
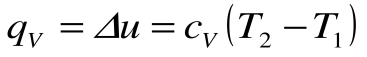 .
.
Таким образом, подведенная к газу в изохорном процессе теплота целиком идет на увеличение его внутренней энергии. Для ТП 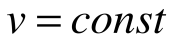 коэффициент распределения теплоты
коэффициент распределения теплоты 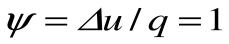 , теплоемкость
, теплоемкость  и показатель политропы:
и показатель политропы:
 .
.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
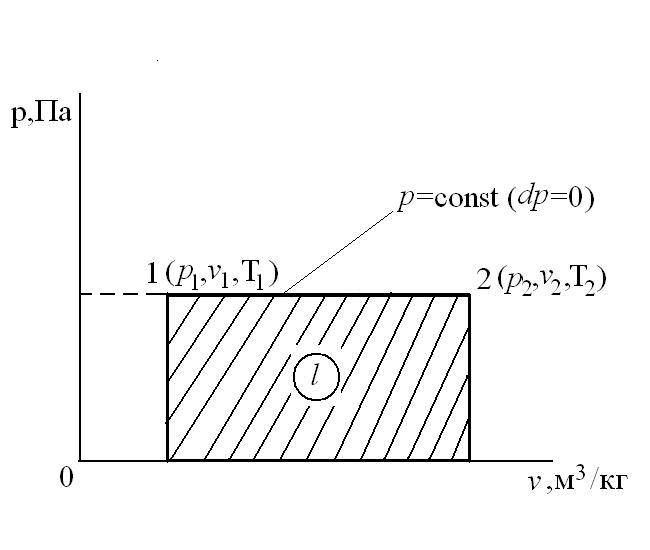
Соотношение между параметрами в процессе р=const: 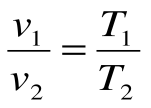 - закон Гей-Люссака, т.к.:
- закон Гей-Люссака, т.к.:  ,
,  и
и 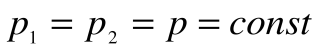 .
.
Работа расширения 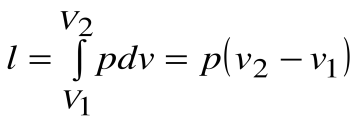 . Т.к.
. Т.к. 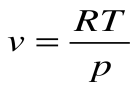 , то
, то 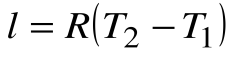 .
.
Следовательно, удельная газовая постоянная R - это работа, совершаемая 1кг газа в процессе p=const при его нагревании на один градус. Размерность R: Дж/кгК. Уравнение 1-го закона термодинамики в этом случае имеем вид:
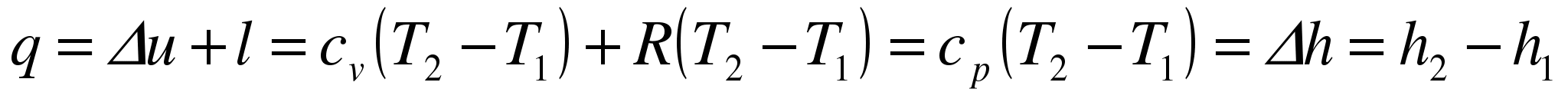 .
.
Таким образом, вся теплота, подведенная к газу в изобарном процессе, расходуется на увеличение его энтальпии.
Коэффициент распределения теплоты в процессе р=const равен:
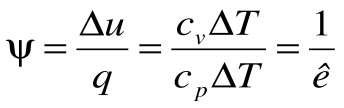 ,
, 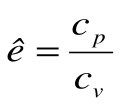 .
.
В T-s координатах взаимное положение изобары и изохоры имеет вид:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
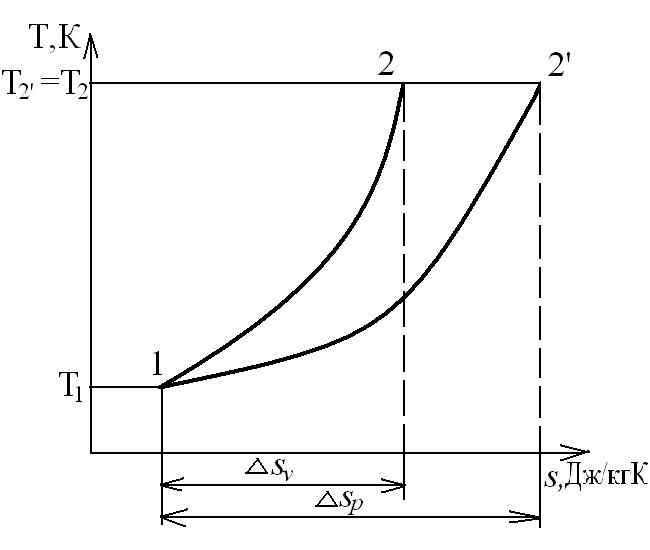
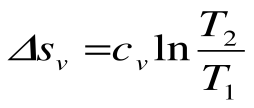 ,
, 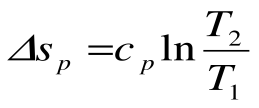 , т.е. изобара более пологая логарифмическая кривая в T-s координатах, чем изохора.
, т.е. изобара более пологая логарифмическая кривая в T-s координатах, чем изохора.
Изотермический процесс – это процесс сообщения или отнятия теплоты от газа при постоянной температуре
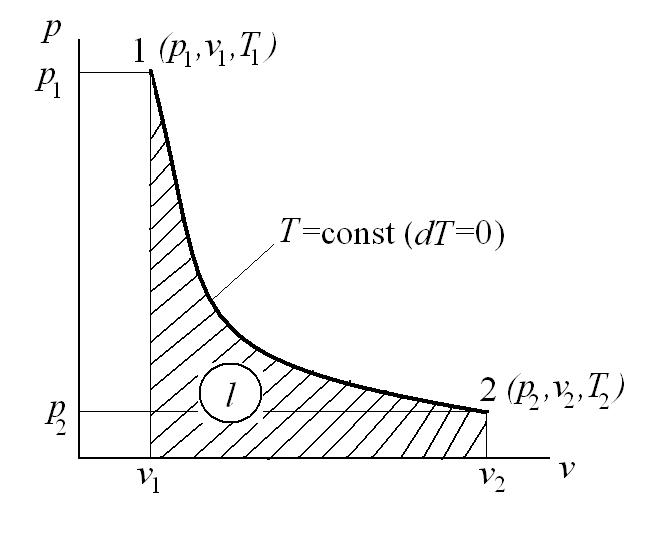
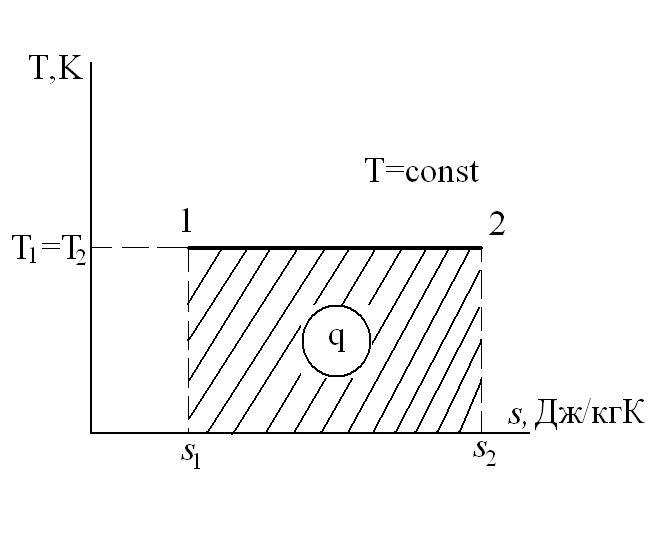
При Т=const из уравнения состояния  имеем:
имеем: 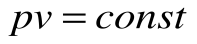 - это уравнение изотермического процесса является уравнением равнобокой гиперболы.
- это уравнение изотермического процесса является уравнением равнобокой гиперболы.
Тогда 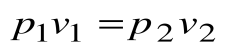 , и
, и 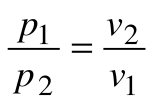 - закон Бойля-Мариотта.
- закон Бойля-Мариотта.
Из уравнения 1-го закона термодинамики 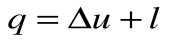 при
при 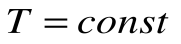 имеем:
имеем:
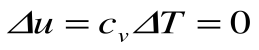 и q=l, т.е. вся теплота, сообщаемая газу в изотермическом процессе, целиком идет на работу расширения газа.
и q=l, т.е. вся теплота, сообщаемая газу в изотермическом процессе, целиком идет на работу расширения газа.
Изменение энтальпии в процессе T=const равно:
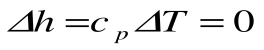 .
.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Работа расширения 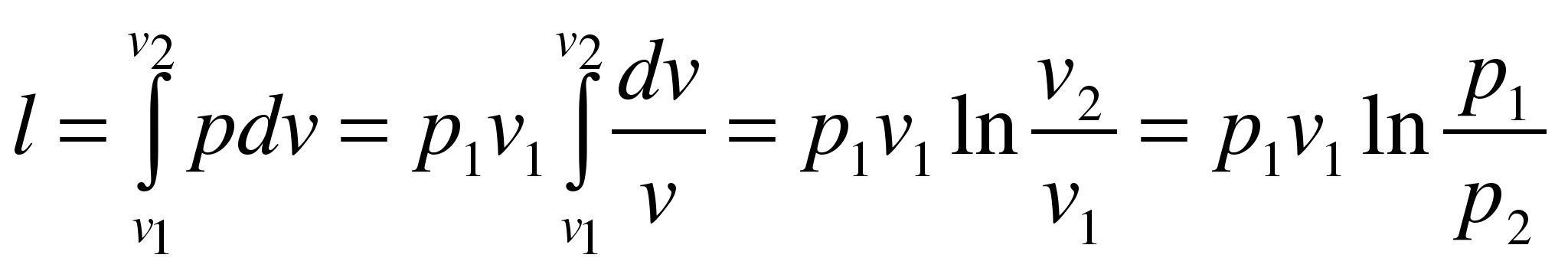 .
.
Коэффициент распределения теплоты
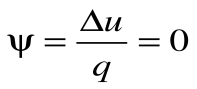 .
.
Тогда теплоемкость 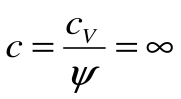 и показатель политропы для процесса T=const будет равен
и показатель политропы для процесса T=const будет равен 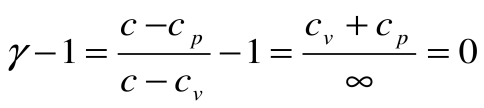 , т.е.
, т.е. 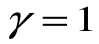 .
.
Адиабатный процесс – это процесс, протекающий без внешнего теплообмена, т.е. q =0 и 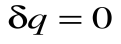 (на конечном и бесконечно малом участке процесса).
(на конечном и бесконечно малом участке процесса).
Если записать для этого случая уравнения 1-го закона термодинамики в виде:
1. 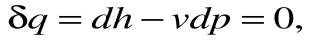 или
или 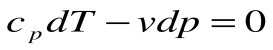 ,
,
2.  или
или 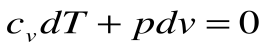 , то после деления (1) на (2) получим:
, то после деления (1) на (2) получим:
 - показатель адиабаты.
- показатель адиабаты.
Тогда после интегрирования выражения 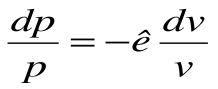 для конечного процесса 1-2 будем иметь
для конечного процесса 1-2 будем иметь  , или
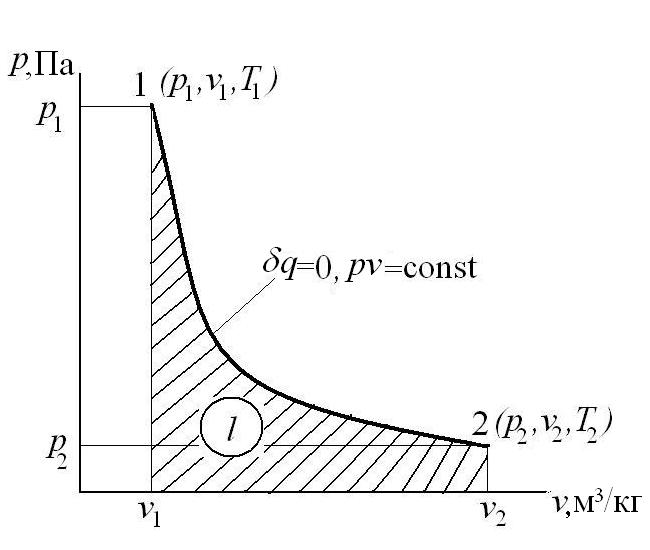
, или 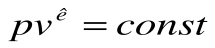 - это есть уравнение адиабатного процесса в p-v -координатах, которое является уравнением неравнобокой гиперболы.
- это есть уравнение адиабатного процесса в p-v -координатах, которое является уравнением неравнобокой гиперболы.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
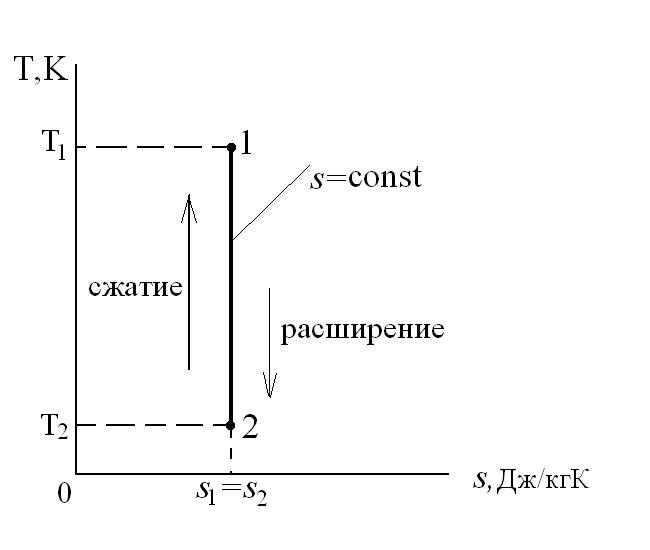
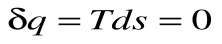 , т.к. Т
, т.к. Т 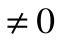 , то ds =0 и s=const. Таким образом, адиабатный процесс с идеальным газом есть изоэнтропийный процесс.
, то ds =0 и s=const. Таким образом, адиабатный процесс с идеальным газом есть изоэнтропийный процесс.
Для теплового двигателя цикл Карно – прямой цикл, состоящий из двух адиабат и двух изотерм, а для тепловых трансформаторов используется обратный цикл Карно. Тепловые машины, работающие по циклу Карно, имеют наибольшие значения термических кпд по сравнению с любым другим циклом при одинаковых предельных температурах цикла Т 1 и Т 2.
Рассмотрим прямой цикл Карно.
Графически в p-v и T-s координатах этот цикл можно представить в виде:
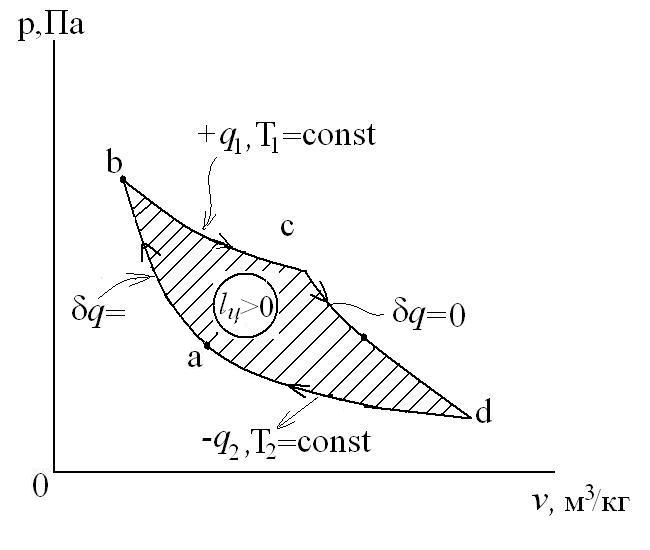
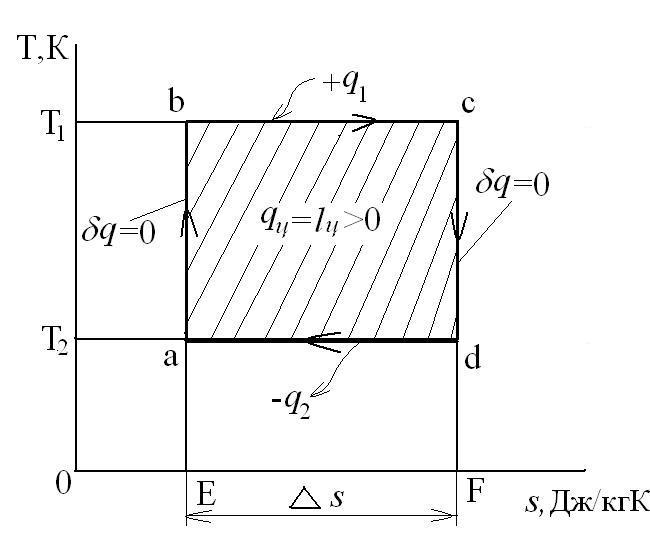
где ab – адиабатное сжатие ТРТ;
bc – подвод теплоты q 1 в изотермическом процессе при Т 1=const;
cd – адиабатное расширение ТРТ;
da – отвод теплоты 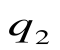 в холодильник при Т 2=const;
в холодильник при Т 2=const;
q 1 = площадь bсFEb – теплота, затраченная на совершение цикла 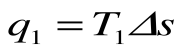 .
.
q 2 = площадь adFЕa – теплота, отведенная в холодильник 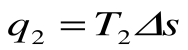 .
.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Тогда термический кпд прямого цикла Карно будет равен:
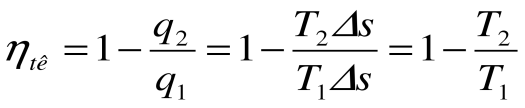 .
.
Таким образом, термический кпд цикла Карно зависит только от предельных температур источника и холодильника и не зависит от рода рабочего тела. (Первая теорема Карно). Температура Т 1 и Т 2 являются основными параметрами цикла Карно, которые полностью определяют этот цикл.
При Т 1= Т 2 термический кпд цикла Карно 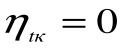 , т.е. превращение теплоты в работу невозможно.
, т.е. превращение теплоты в работу невозможно.
При Т 2=0 или Т 1= 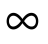
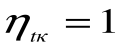 , что невыполнимо. Следовательно, в цикле Карно термический кпд цикла всегда меньше единицы:
, что невыполнимо. Следовательно, в цикле Карно термический кпд цикла всегда меньше единицы: 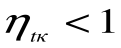 . Таким образом, для прямого цикла Карно
. Таким образом, для прямого цикла Карно 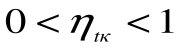 .
.
Любое заключение, вытекающее из анализа прямого цикла Карно, можно рассматривать как формулировку второго закона термодинамики.
Задача №1
В двух разобщенных между собой теплоизолированных сосудах А и В содержатся газы, в сосуде А – аргон, в сосуде В – водород, объем сосуда А – 150 л, сосуда В – 250 л. Давление и температура аргона – р 1, t 1, водорода – р 2, t 2. Определить давление и температуру, которые установятся после соединения сосудов и смешения газов. Теплообменом с окружающей средой пренебречь
Дано:
А-аргон (Ar)
В-водород (H2)
P1=2.6*106 Па
P2=0.4*106 Па
T1=593 K
T2=293 K
Найти: Тсм-?; Рсм-?
Решение.
Vсм=V1+V2;
Mсм=M1+M2;
Uсм=U1+U2;
U1=Cv1·M1·T1
Cv1= 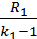 ; M1=
; M1= 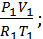
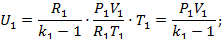
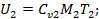


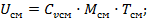
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
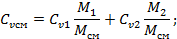
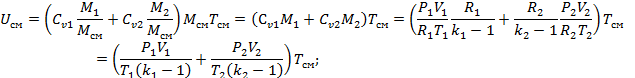
Подставим в первое уравнение:
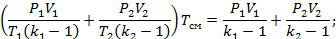
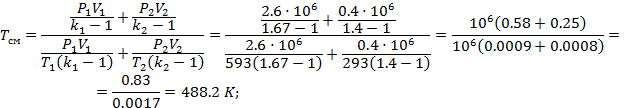
Воспользуемся уравнением состояния:
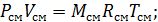
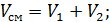
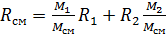 , где R1 и R2-газовые постоянные смешивающихся газов
, где R1 и R2-газовые постоянные смешивающихся газов
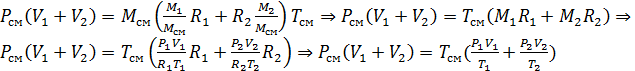 ,
,
тогда
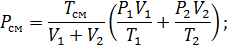
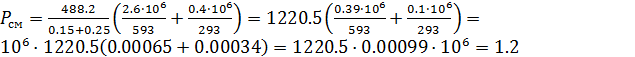 МПа
МПа
Pсм=1.2 МПа
Tсм=488,2 К
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Задача №20
Двухступенчатый поршневой компрессор всасывает 15 м3/мин газа при давлении р 1 и температуре t 1 и сжимает его до конечного давления р 2. Между ступенями установлен промежуточный холодильник, в котором газ охлаждается при постоянном давлении до начальной температуры. Определить теоретическую мощность, затрачиваемую на привод компрессора, количество теплоты, которое должно быть отведено от газа в каждой ступени и в промежуточном холодильнике, если известно, что степень повышения давления одинакова для обеих ступеней и сжатие в них происходит политропно (n = 1,3). Изобразить процесс сжатия в координатах u - p.
Дано:
P1=0.12*106 Па
T1=278 К
P2=0.6*106 Па
n=1.3
газ-H2
V=15.3 м3/мин
Найти: Qст-?; Qхол-?
РЕШЕНИЕ:
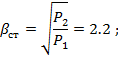
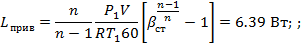
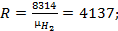 где R- газовая постоянная газа
где R- газовая постоянная газа
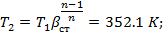
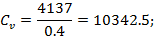
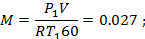
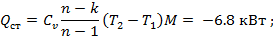
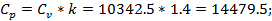

График зависимости:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Раздел 2. «Теплопередача».
Вопрос №7
Потребности в сокращении затрат энергии и материалов, равно как и экономические причины, требуют создания более эффективного теплообменного оборудования. Цель этих требований состоит
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Более эффективная теплопередача может понадобиться также для предотвращения перегрева или разрушений систем при заданной интенсивности тепловыделения.
Термическое сопротивление стенки можно уменьшить путем уменьшения толщины стенки и увеличения коэф. теплопроводности материала; теплоотдача может быть интенсифицирована путем
перемешивания жидкости и увеличения скорости движения; при тепловом излучении - путем повышения степени черноты и t-ры излучающей пов-ти.
Вопрос о путях интенсификации процесса теплопередачи более сложный; правильное его решение может быть получено лишь на основе тщательного анализа частных условий теплопередачи.
Выявив частные термические сопротивления, легко найти и решение задачи об интенсификации теплопередачи. Если частные термические сопротивления различны, то, чтобы увеличить
теплопередачу, достаточно уменьшить наибольшее из них. Если же все частные термические сопротивления одного порядка, то увеличение коэф. теплопередачи возможно за счет уменьшения
любого из сопротивлений.
Способы интенсификации теплопередачи путем увеличения коэф. теплоотдачи:
Приемы интенсификации теплоотдачи можно подразделить на пассивные (не требующие непосредственных затрат энергии извне) и активные (кот. требуют прямых затрат энергии от внешнего
источника). Пассивные методы вкл. специальную физико-химическую обработку пов-тей, использование шероховатых и развитых пов-тей, устройств, обеспечивающих перемешивание и закручивание
потока, добавление примесей в теплоноситель. Активные методы вкл. механические воздействия, вибрацию пов-тей теплообмена, пульсации потока жидкости или более из этих методов могут быть использованы одновременно (комбинированная интенсификация). Все эти способы направлены на разрушение пограничного ламинарного слоя, опр. интенсивность теплоотдачи.
Тепловая изоляция - всякое покрытие, кот. способствует снижению потери теплоты в окр. среду. Назначение изоляции различно - экономия топлива, создание возможности осуществления технологических процессов или создание санитарных условий труда.
Теплоизоляционными наз. материалы, коэф. теплопроводности кот. при t-ре 50 - 100°С меньше 0,2 Вт/(м,0С). Изоляционные материалы бывают естественные (асбест, слюда, дерево, пробка, опилки) и искусственные (шлаковая вата, изол, асбозурит, асбослюда).
Условия рационального выбора материала для тепловой изоляции трубопроводов. При наложении тепловой изоляции на трубопровод тепловые потери уменьшаются не пропорционально увеличению толщины изоляции, более того, при неправильном выборе материала изоляции тепловые потери возрастут. Это связано с тем, что у изолированного трубопровода увеличивается диаметр и пов-ть теплообмена с окр. средой, что приводит к увеличению теплоотдачи. Рассмотрим общее термическое сопротивление теплопередачи трубопровода, на кот. наложен слой изоляции:
Rобщ = R1 + R2 + Rз + R4
Термическое сопротивление теплоотдачи и теплопроводности стенки трубы R2 = с увеличением dиз останутся неизменными, при этом термическое сопротивление теплопроводности изоляционного слоя Rз = будет возрастать, а термическое сопротивление теплоотдачи R4 = - уменьшаться.
Для того чтобы выяснить, как будет изменяться Rобщ при изм. диаметра изоляции, исследуем Rобщ как функцию dиз, Возьмем частную производную от Rобщ по dиз и приравняем к нулю: Отсюда:
dиз = dиз.КР = 2(λиз/a2) Значение dиз.КР наз. критическим диаметром тепловой изоляции. Критический диаметр изоляции не зависит от диаметра трубы, он тем меньше, чем меньше λиз больше a2. Если dиз увеличивается, но остается меньше dиз.КР, то тепловые потери увеличиваются. При dиз = dиз.КР тепловые потери максимальны. Дальнейшее увеличение dиз ведет к снижению потерь. Чтобы изоляция работала эффективно необходимо dиз > dКр = 2(λиз/a2), т.е. dиз.КР < d2, или λиз < a2d2/2 - условие рационального подбора материала для тепловой изоляции трубопроводов, где d2 - наружный диаметр трубопровода, а a2 - коэф. теплоотдачи от внешней пов-ти изоляции к окр. среде. Если условие не выполнено, то при нанесении тепловой изоляции на трубопровод тепловые потери будут не снижаться, а расти.
При теплоотдаче в условиях свободной конвекции и t-ре окр. среды = 20 °С толщину изоляции трубопроводов с точностью до 3-5% опр. по формуле: δиз = 2.75, где δиз - толщина изоляции, мм; d1 - диаметр трубопровода, мм; tс1 - его t-ра; λ из - коэф. теплопроводности изоляции; ql- линейная плотность теплового потока. Если t-ра окр. среды выше 20 °С, то тепловые потери уменьшаются: на каждые 5°С повышения t-ры тепловые потери снижаются ~ на 1.5%.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Закон Планка
Этот закон является одним из основных законов излучения и устанавливает зависимость интенсивности излучения J0 абсолютно черного тела от его температуры и длины волны:
J0 =dE0/dλ = С1λ-5[ехр(С2/λT,)-1]-1, (1)
где С1 и С2 — постоянные величины; λ-длина волны; Т - абсолютная температура тела; индекс «0» показывает, что рассматривается излучение абсолютно черного тела.
Графическая интерпретация закона Планка представлена на рис.1 Для любой температуры тела интенсивность его излучения возрастает от нуля (при λ = 0) до своего максимального значения при определенной длине волн, а затем убывает до нуля (при λ = 8).
При повышении температуры тела интенсивность его излучения значительно увеличивает-
Рис.1
ся. Свойствами теплового излучения лучистая энергия обладает в диапазоне длин волн от 0,8 до 40 мкм.
Так как закон Планка получен для абсолютно черного тела, то для реальных тел он выражает максимально возможную интенсивность излучения.
Закон Вина
Этот закон представляет один из предельных случаев закона Планка, соответствующий малой величине произведения λT. В этом случае в уравнении (1) можно пренебречь единицей, поэтому
J0 =dE0/dλ = С1λ-5[ехр(С2/λT,)-1]-1 (2)
Для определения максимумов в интенсивности теплового излучения находим производную функции по длине волны и приравниваем ее нулю. В результате получаем
λ maxT= 2,898*10-3, мК. (3)
В этом уравнении λmax — длина волны, соответствующая максимальной интенсивности теплового излучения. Зависимость (3) выражает закон смещения Вина, согласно которому максимальная величина спектральной интенсивности теплового излучения при повышении температуры тела смещается в сторону более коротких волн (пунктирная линия на рис. 1).
Закон Стефана—Больцмяна
Используя закон Планка, можно найти плотность интегрального излучения абсолютно черного тела:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
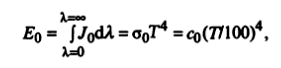 (4)
(4)
где σ0 = 5,67 * 10-8 Вт/м2К4) — константа излучения абсолютно черного тепа; C0 = 5,67 Вт/(м2,К4) — коэффициент излучения абсолютно черно-
Индекс «0» в формуле (4) указывает на то, что рассматривается излучение абсолютно черного тела.
Уравнение (4) было экспериментально получено Стефаном, а затем теоретически обосновано Больцманом,
Реальные тела не являются абсолютно черными, в действительности многие из них можно считать серыми телами. У серых тел собственное тепловое излучение также пропорционально абсолютной температуре в четвертой степени, но энергия излучения меньше, чем у абсолютно черного тела при той же температуре. Закон Стефана—Болцмана для серых тел приобретает вид
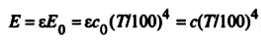
где ε = Е/Е0 = с/с0 < 1,0 — интегральная или средняя степень черноты серого тела; с — коэффициент излучения серого тела.
Степень черноты зависит не только от физических свойств тела, но и от состояния его поверхности (шероховатость) и температуры.
Для многих используемых в технике поверхностей зависимость е от температуры достаточно слабая, В литературных источниках e иногда называют интегральным коэффициентом излучения тела. Для некоторых веществ численные значения ε приведены в табл.
Закон Кирхгофа.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Из закона Кирхгофа следует, что ε = А, т.е. коэффициент поглощения численно равен степени черноты данного тела.
Закон Ламберта
Распределение плотности теплового излучения, испускаемого абсолютно черным телом, по отдельным направлениям неодинаково и определяется законом косинусов Ламберта в виде
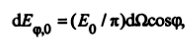
где Eφ,0— плотность излучения, соответствующая углу φ;dΩ — элементарный телесный угол, под которым из данной точки излучающего тела видна элементарная площадка на поверхности полусферы, имеющей центр в этой точке; φ — угол между нормалью к излучающей поверхности и направлением излучения.
Задача №8
На реальной теплотехнической установке происходит процесс теплоотдачи при вынужденном движении потока воздуха в трубе круглого сечения диаметром D, средняя температура воздуха t в, расход воздуха М в =12 кг/с. Для экспериментального изучения теплоотдачи была создана модель, в которой движется жидкость, имеющая коэффициент температуропроводности a м = 0,8·10 -6 м2/с. Какова должна быть скорость жидкости w м и кинематический коэффициент вязкости νм для обеспечения подобия процессов теплообмена, если геомет