Законы распределения случайных величин
В этом параграфе мы изучим некоторые конкретные случайные величины, часто используемые в теории вероятностей, математической статистике и их приложениях.
Биномиальное распределение
Случайная величина с биноминальным законом распределения возникает в схеме Бернулли. Пусть проводится серия  независимых испытаний, причем каждое испытание имеет два исхода: «событие
независимых испытаний, причем каждое испытание имеет два исхода: «событие  появилось» или «событие
появилось» или «событие  не появилось». Вероятность появления события
не появилось». Вероятность появления события  в каждом отдельном испытании равна
в каждом отдельном испытании равна  .
.
Определение. Дискретная случайная величина  , возможными значениями которой являются частоты появления события
, возможными значениями которой являются частоты появления события  в
в  независимых испытаниях
независимых испытаниях  , а вероятность соответствующих значений определяются по формуле Бернулли
, а вероятность соответствующих значений определяются по формуле Бернулли

называется биномиальной случайной величиной с параметрами  и
и  .
.
Таким образом, закон распределения биномиальной случайной величины можно записать в виде таблицы 1.
Таблица 1.

| … | 
| ||

| 
| 
| … | 
|
Свойства биномиального закона распределения
Свойство 1. Сумма вероятностей всех возможных значений биномиальной случайной величины равна единице, т.е.
 .
.
Доказательство. Так как по определению биномиального закона распределения
 ,
,
то, согласно разложению степени бинома по формуле Ньютона, имеем
 . ●
. ●
Из этого свойства вытекает название биномиального распределения вероятностей.
Свойство 2. Если частота  возрастает то нуля до некоторого значения частоты
возрастает то нуля до некоторого значения частоты  , то вероятность соответствующих значений также возрастают до величины
, то вероятность соответствующих значений также возрастают до величины  , а при дальнейшем возрастании частоты
, а при дальнейшем возрастании частоты  вероятности соответствующих значений убывают.
вероятности соответствующих значений убывают.
Доказательство. Выведем условия, при которых вероятности  с ростом
с ростом  возрастают, т.е. удовлетворяют неравенству
возрастают, т.е. удовлетворяют неравенству
 или
или  . (1)
. (1)
Так как
 ;
;  ,
,
то из равенства (1) получаем
 ,
,
откуда находим

 (2)
(2)
Следовательно, при возрастании  от нуля до
от нуля до  вероятности соответствующих значений монотонно возрастают.
вероятности соответствующих значений монотонно возрастают.
Аналогично выводим условие, при котором вероятности соответствующих значений  с ростом
с ростом  убывают.
убывают.
Если
 ,
,
то
 . (3)
. (3)
Так как
 ,
,
то
 ,
,
откуда находим

 . (4)
. (4)
Следовательно, при возрастании  от
от  до
до  вероятности соответствующих значений монотонно убывают.
вероятности соответствующих значений монотонно убывают.
Таким образом, существует частота, которой соответствует наибольшая вероятность.
Определение. Частота, которой соответствует наибольшая вероятность при заданных параметрах  и
и  называется наивероятнейшей частотой.
называется наивероятнейшей частотой.
Наивероятнейшую частоту обычно обозначают  .
.
Свойство 3. Наивероятнейшая частота определяется из двойного неравенства
 .
.
Доказательство. Из определения наивероятнейшей частоты получаем
 и
и  .
.
Согласно свойству 2, имеем
 ; (5)
; (5)
 . (6)
. (6)
Объединив неравенства (5) и (6) получаем двойное неравенство для определения наивероятнейшей частоты 
 .
.
Если  целое число, то наивероятнейшая частота принимает два значения:
целое число, то наивероятнейшая частота принимает два значения:
 или
или  .
.
Если  дробное число, то наивероятнейшая частота имеет единственное значение, которое равно целой части числа
дробное число, то наивероятнейшая частота имеет единственное значение, которое равно целой части числа  , т.е.
, т.е.
 .
.
Из рассмотренных свойств биномиального закона распределения следует, что полигон распределения вероятностей биномиальной случайной величины имеет вид
|
 целое число целое число
|
Свойство 4. Числовые характеристики биноминальной случайной величины вычисляются по формулам
 ,
,  ,
,  .
.
Доказательство. Математическое  можно найти, пользуясь определением математического ожидания случайной величины, что приводит к громоздким вычислениям.
можно найти, пользуясь определением математического ожидания случайной величины, что приводит к громоздким вычислениям.
Более простой путь состоит в следующем. Свяжем с  ым испытанием случайную величину
ым испытанием случайную величину  , которая сможет принимать только два значения:
, которая сможет принимать только два значения:
 , если в
, если в  ом испытании событие
ом испытании событие  произошло, вероятность этого значения
произошло, вероятность этого значения 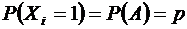 ;
;
 , если в
, если в  ом испытание событие
ом испытание событие  не произошло,
не произошло,  .
.
Так как испытания в схеме Бернулли независимы, то независимы случайные величины  , причем закон распределения каждой из них имеет вид
, причем закон распределения каждой из них имеет вид

| 
| ||

| 
| 
|
Найдем математическое ожидание случайной величины 


Найдем теперь дисперсию
 .
.
Очевидно, частота  наступления события
наступления события  в
в  независимых испытаниях равна сумме рассматриваемых случайных величин
независимых испытаниях равна сумме рассматриваемых случайных величин  .
.
 .
.
Пользуясь свойством 4 математических ожиданий, получаем

Пользуясь свойством 4 дисперсии, находим
 .
.
По определению среднего квадратического отклонения
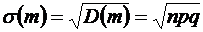 .
.
Итак, доказано, что числовые характеристики частоты вычисляются по формулам:
 , (7)
, (7)
 , (8)
, (8)
 . (9)
. (9)
Следствие. Числовые характеристики относительной частоты  вычисляются по формулам:
вычисляются по формулам:
 ,
,  ,
,  .
.
Доказательство. Воспользовавшись формулой 7 и свойством 2 математического ожидания, получаем
 .
.
Из формулы 8 и второго свойства дисперсии, следует
 .
.
Согласно определению среднего квадратического отклонения случайной величины, получаем
 . ●
. ●

