Свойство 1. Областью определения дифференциальной функции нормального закона распределения является все множество действительных чисел
Доказательство. Следует из вида дифференциальной функции распределения нормального закона.
Свойство 2. Областью изменения дифференциальной функции нормального закона распределения является промежуток
 .
.
Доказательство. Так как, с одной стороны, 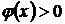 при
при  , а, с другой стороны, функция
, а, с другой стороны, функция  имеет максимум, причем
имеет максимум, причем  (см. свойство 5), то областью изменения функции
(см. свойство 5), то областью изменения функции  является промежуток
является промежуток 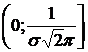 .
.
Свойство 3. Нормальная кривая симметрична относительно прямой 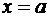 .
.
Доказательство. Введем замену переменной  . Тогда дифференциальная функция распределения запишется в виде
. Тогда дифференциальная функция распределения запишется в виде
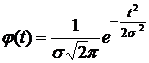 .
.
Функция 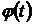 является четной. Известно, что график четной функции симметричен относительно прямой
является четной. Известно, что график четной функции симметричен относительно прямой 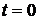 . Следовательно, график функции
. Следовательно, график функции  симметричен относительно прямой
симметричен относительно прямой 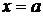 .
.
Свойство 4. Нормальная кривая является непрерывной на всей числовой прямой.
Доказательство. Функция  является непрерывной по теореме о непрерывности элементарной функции.
является непрерывной по теореме о непрерывности элементарной функции.
Свойство 5. Нормальная кривая имеет максимум в точке 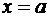 , причем
, причем  .
.
Доказательство. Найдем производную функции 
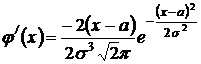 .
.
Из уравнения
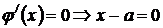
находим стационарную точку  . Стационарная точка разбивает область определения функции
. Стационарная точка разбивает область определения функции  на промежутки монотонности.
на промежутки монотонности.

| Т.к. на промежутке 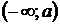 производная производная  , то на этом промежутке функция , то на этом промежутке функция  возрастает.
На промежутке возрастает.
На промежутке 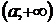 производная производная  , поэтому на этом промежутке функция убывает. , поэтому на этом промежутке функция убывает.
|
Следовательно в точке  функция имеет максимум
функция имеет максимум
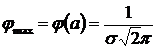 .
.
Свойство 6. Нормальная кривая имеет две точки перегиба с абсциссами  , ордината точек перегиба
, ордината точек перегиба
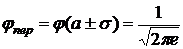 .
.
Доказательство. Найдем вторую производную функции 
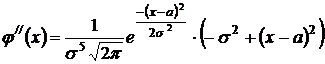
Из уравнения
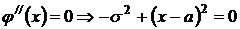 ,
,
получаем две критические точки второго порядка

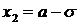 .
.
Критические точки второго порядка разбивают область определения функции  на промежутки выпуклости и вогнутости.
на промежутки выпуклости и вогнутости.
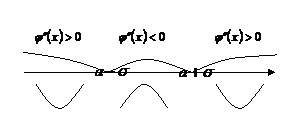
| Определяя знак 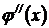 на каждом из промежутков делаем вывод: на промежутках на каждом из промежутков делаем вывод: на промежутках 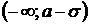 и и 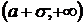 вторая производная вторая производная  , поэтому функция , поэтому функция  на этих промежутках вогнута; на этих промежутках вогнута;
|
на промежутке 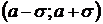 вторая производная
вторая производная 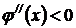 , поэтому функция на этом промежутке выпуклая. Точки
, поэтому функция на этом промежутке выпуклая. Точки 
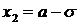 являются точками перегиба. Находим ординаты точек перегиба
являются точками перегиба. Находим ординаты точек перегиба
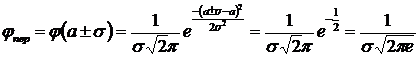 .
.
Свойство 7. Нормальная кривая имеет одну горизонтальную асимптоту, которой является ось  .
.
Доказательство. Так как  , то прямая
, то прямая 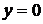 , т.е. ось
, т.е. ось  является двусторонней горизонтальной асимптотой графика функции
является двусторонней горизонтальной асимптотой графика функции  .
.
На основании проведенного исследования строим график дифференциальной функции распределения нормального закона.

| Кривую нормального закона распределения называют нормальной или гауссовой кривой. Она имеет симметричный холмообразный вид. Точка  называется центром рассевания. По мере удаления от точки называется центром рассевания. По мере удаления от точки  плотность плотность  уменьшается и при уменьшается и при  кривая распределения асимптотически приближа-ется к оси абсцисс. кривая распределения асимптотически приближа-ется к оси абсцисс.
|
Зависимость нормальной кривой от значений параметров закона  и
и 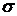 .
.
Рассмотрим изменения, которые происходят в расположении и виде нормальной кривой при изменении параметров  и
и 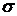 .
.
Параметр  характеризует положение нормальной кривой.
характеризует положение нормальной кривой.
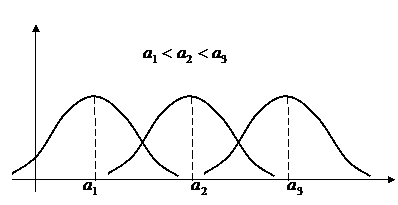
| При изменении параметра 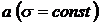 изменяется центр симметрии распределе-ния, поэтому нормальная кривая, не меняя своей формы, смещается влево при уменьшении параметра изменяется центр симметрии распределе-ния, поэтому нормальная кривая, не меняя своей формы, смещается влево при уменьшении параметра  и смещается вправо при увеличении параметра и смещается вправо при увеличении параметра  . .
|
Параметр 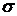 определяет форму нормальной кривой.
определяет форму нормальной кривой.

| При изменении параметра 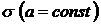 меняется форма нормальной кривой. При увеличении меняется форма нормальной кривой. При увеличении 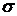 ордината максимума ордината максимума  уменьшается, точки перегиба уменьшается, точки перегиба 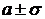 удаляются от центра рассеивания, а так как площадь под кривой должна оставаться удаляются от центра рассеивания, а так как площадь под кривой должна оставаться
|
равной единице, то нормальная кривая растягивается вдоль оси  , принимает более пологий вид. При уменьшении
, принимает более пологий вид. При уменьшении 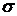 ординат максимума увеличивается, точки перегиба приближаются к центру рассеивания. Нормальная кривая, вытягиваясь вдоль оси
ординат максимума увеличивается, точки перегиба приближаются к центру рассеивания. Нормальная кривая, вытягиваясь вдоль оси 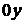 , приобретает более сжатую форму.
, приобретает более сжатую форму.
Вывод. Параметр 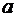 характеризует положение нормальной кривой на координатной плоскости, а параметр
характеризует положение нормальной кривой на координатной плоскости, а параметр 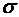 определяет форму нормальной кривой.
определяет форму нормальной кривой.
Определение. Нормальный закон распределения случайной величины с параметрами 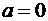 и
и 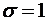 называется стандартным или нормированным и обозначается
называется стандартным или нормированным и обозначается 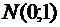 , соответствующаяему нормальная кривая называется стандартной или нормированной нормальной кривой.
, соответствующаяему нормальная кривая называется стандартной или нормированной нормальной кривой.