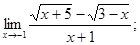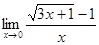Вычисление пределов любых функций начинают с подстановки в функцию, стоящую под знаком предела, того значения, к которому стремится х, и вычисления значения получившегося числового выражения.
1) Непосредственное вычисление значения функции под знаком предела в данной точке (вычисление предела непрерывной функции).
ПРИМЕРЫ:
;
.
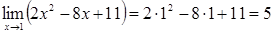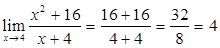ЗАМЕЧАНИЕ: Однако в некоторых случаях в результате вычислений получают выражение вида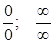 
; 
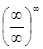и другие - такие выражения называют неопределенностями, которые «раскрывают» каждый раз специальным образом, после чего становиться возможным вычисление предела данной функции. Рассмотрим примеры таких пределов и способы их преобразований.
2) В случае неопределенности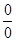 
необходимо числитель и знаменатель разложить на множители и сократить дробь.
ПРИМЕР:
;
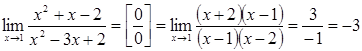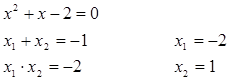
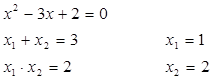
Замечание: Способы разложения на множители.
1. Формулы сокращенного умножения.
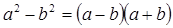- разложение на множители разности квадратов;
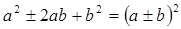- разложение на множители квадрата суммы-разности;
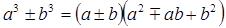- разложение на множители суммы- разности кубов.
2. Способ группировки (возможен при наличии четного числа слагаемых):
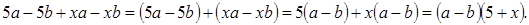
3. Разложение квадратного трехчлена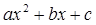 
на множители.
Сначала необходимо решить соответствующее квадратное уравнение
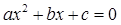. Для этого используем формулу:
Если: 
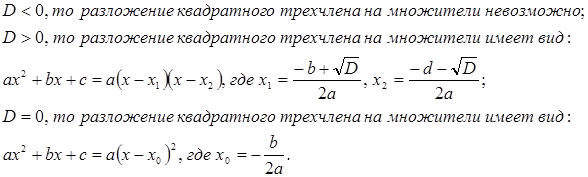Вычислять корни полного приведенного квадратного уравнения можно, пользуясь также обратной теоремой Виета:
Если: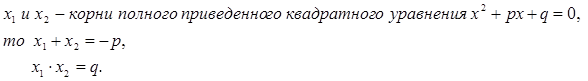 
3) В случае неопределенности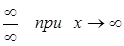 
необходимо и числитель и знаменатель дроби разделить на старшую степень, при этом, если старшие степени многочленов в числителе и знаменателе одинаковы, то предел равен отношению коэффициентов при старших степенях; иначе, он равен нулю или бесконечности 
.
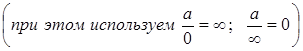ПРИМЕРЫ:
.
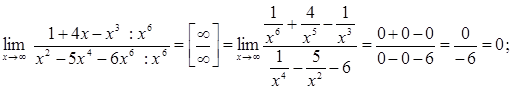
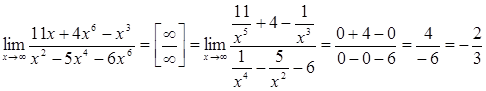В случае второго предела, используя данные рекомендации, будем действовать короче:
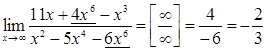
4) Если имеем неопределенность вида 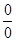в случае иррациональности необходимо и числитель, и знаменатель умножить на выражение, сопряженное иррациональности, упростить и сократить дробь, учитывая, что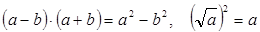 
сопряженные
ПРИМЕР:
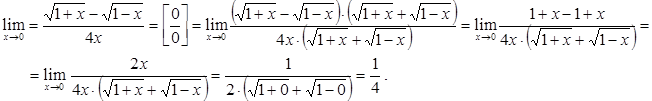
ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ:
№ 1 Т.к. функции в указанных точках непрерывны, для нахождения предела достаточно найти значение функции в точке.
Найти предел функции:
1) 
;
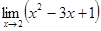2) 
;
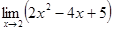3) 
.
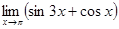№ 2 Имеем неопределенность вида 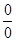. Чтобы избавиться от неопределенности, нужно числитель и знаменатель разложит на множители и сократить дробь.
Найти предел функции:
1) 
;
2) 
;
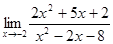3) 
;
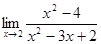4) 
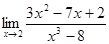
№ 3 Для вычисления предела в случае неопределенности вида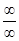 
при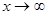 
числитель и знаменатель дроби необходимо поделить на старшую степень переменной. При этом, если многочлены в числителе и в знаменателе одной степени, то предел равен отношению коэффициентов при старших степенях; если разных степеней; то предел равен 0 или 
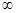(учитываем, что 
).
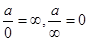Найти предел функции:
1) 
;
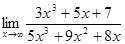2) 
;
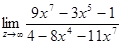3) 
;
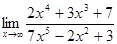4) 
.
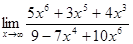№ 4 Чтобы избавиться от неопределенности вида 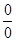в случае иррациональности (выражение содержит радикал) в числителе или знаменателе, надо и числитель, и знаменатель умножить на выражение, сопряженное иррациональности, упростить и сократить дробь (a-b и a+b – сопряженные выражения; (a-b)(a+b)=a2-b2; 
).
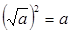Найти предел функции:
1) 
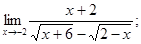
2) 
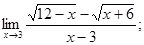
3) 
4) 
