Практическое занятие №1-2.
12.1 В лоторее 2000 билетов. На один билет падает выигрыш 1000 руб., на четыре билета – 500 руб., на десять билетов – 200 руб., на двадцать билетов – 100 руб., на 100 билетов – 50 руб., на 200 билетов – 10 руб., остальные билеты невыигрышные. Какова вероятность выиграть по одному билету не менее 100 руб.
12.2 Задумано двузначное число. Найти вероятности того, что задуманным числом окажется: а) случайно названное двузначное число;
б) случайно названное двузначное число, цифры которого различны.
12.3 Участники жеребьёвки тянут из ящика жетоны с номерами от 1 до 35. Найти вероятности того, что номер первого наудачу извлечённого жетона: а) не содержит цифру 2;
б) содержит цифру 3; в) является чётным числом; г) является числом, кратным 3 (делится на 3 без остатка).
12.4 Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу, извлеченный кубик имеет окрашенных граней: а) одну; б) две; в) три; г) ни одной.
12.5 Монета подброшена 2 раза. Найти вероятности того, что герб выпадет: а) два раза; б) один раз; в) ни одного раза; г) хотя бы один раз.
12.6 Бросают три монеты. Найти вероятности того, что герб появится: а) только на одной монете; б) на всех монетах; в) хотя бы на одной монете; г) не менее чем на двух монетах.
12.7 Бросают две игральные кости. Найти вероятности следующих событий: а) сумма выпавших очков равна семи; б) произведение выпавших очков равно шести; в) сумма выпавших очков больше их произведения; г) сумма выпавших очков равна восьми, если известно, что их разность равна четырем.
12.8 В первом ящике находятся шары с номерами от 1 до 5, а во втором – с номерами от 6 до 10. Из каждого ящика вынимают по одному шару. Найти вероятности того, что: а) сумма номеров вынутых шаров равна девяти; б) произведение номеров вынутых шаров больше 20; в) сумма номеров вынутых шаров больше их произведения; г) абсолютная величина разности номеров вынутых шаров равна четырём.
12.9 Имеется 5 лоторейных билетов стоимостью по 100 руб., 3 билета по 300 руб. и 2 билета по 500 руб. Наудачу выбирают 3 билета. Найти вероятности того, что: а) все три выбранных билета в сумме стоят 700 руб.; б) все три выбранных билета имеют одинаковую стоимость.
12.10 Наудачу берут три монеты из пяти таких: две монеты по 5 коп., две – по 10 коп., одна – по 50 коп. Найти вероятность того, что общее достоинство всех вынутых монет превысит 60 коп.
12.11 В урне 6 белых и 5 чёрных шаров. Наудачу вынимают четыре шара. Найти вероятность того, что среди выбранных окажется три чёрных шара.
12.12 В цехе работают шесть мужчин и четыре женщины. По табельным номерам наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины.
12.13 Студент пришел на экзамен, зная лишь 20 вопросов из 25. Какова вероятность того, что студент знает ответ на оба вопроса, заданные ему экзаменатором.
12.14 Из колоды в 36 карт вынимают наудачу 3 карты. Найти вероятность того, что среди них окажется хотя бы один туз.
12.15 Партия из 100 деталей подвергается выборочному контролю. Условием непригодности всей партии является наличие хотя бы одной бракованной детали среди 5 проверяемых. Найти вероятность того, что данная партия будет принята, если она содержит 5% бракованных деталей.
12.16 Двенадцать студентов получили путёвки в 4 санатория: 3 – в первый, 3 – во второй, 2 – в третий и 4 – в четвёртый. Какова вероятность того, что данные три студента поедут отдыхать в один санаторий.
12.17 Для производственной практики на 30 студентов предоставлено 15 мест в Наб.Челнах, 8 – в Елабуге и 7 – в Нижнекамске. Какова вероятность того, что два определённых студента попадут на практику в один город.
12.18 У туристов было 2 банки с мясом, 3 банки с овощами, 4 банки с кашей. Во время дождя надписи на банках были смыты. Туристам нужно открыть три банки. Какова вероятность того, что все три открытые банки будут отличаться содержимым.
12.19 На ТЭЦ 15 сменных инженеров, из них 3 женщины. В смену занято 3 человека. Найти вероятности того, что в случайно выбранную смену: а) мужчин окажется не менее двух; б) окажется хотя бы одна женщина.
12.20 В урне 2 чёрных, 3 синих и 5 белых шаров. Наудачу (без возвращения) вынимают 3 шара. Найти вероятность того, что: а) все вынутые шары одного цвета; б) все вынутые шары разного цвета.
12.21 Среди кандидатов в студсовет факультета 3 первокурсника, 5 второкурсников и 7 третьекурсников. Из этого состава наудачу выбирают 5 человек на предстоящую отчётно-выборную конференцию. Найти вероятности того, что: а) все первокурсники попадут на конференцию; б) будет выбран один первокурсник, два второкурсника и два третьекурсника.
12.22 В группе из 30 студентов на контрольной работе по «Теории вероятностей» 6 студентов получили оценку «отлично», 10 – «хорошо», 9 - «удовлетворительно», остальные – «неудовлетворительно». Найти вероятности того, что: а) все три студента вызванные к доске, имеют по контрольной работе оценку «неудовлетворительно»; б) хотя бы один студент из трёх вызванных к доске имеет оценку «отлично» или «хорошо».
12.23 В коробке смешаны электролампы одинакового размера и формы: по 100Вт – 7 штук; по 75Вт – 13 штук. Вынуты наудачу три лампы. Какова вероятность того, что:
а) они одинаковой мощности; б) хотя бы две из них по 100Вт.
12.24 Среди 25 студентов, из которых 15 девушек, разыгрываются 4 билета в театр, причём каждый может выиграть только один билет. Найти вероятности того, что обладателями билетов станут: а) три юноши и одна девушка; б) хотя бы один юноша.
12.25 В “секретном” замке на общей оси четыре диска, каждый из которых разделен на 5 секторов, на которых написаны различные цифры. Замок открывается только в том случае, если диски установлены так, что цифры на них составляют определенное четырехзначное число. Найти вероятность того, что при произвольной установке дисков замок будет открыт.
12.26 Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
12.27 Из 10 карточек азбуки было составлено слово «МАТЕМАТИКА». Карточки перемешали и по схеме случайного выбора без возвращения отобрали четыре. Найти вероятность того, что из отобранных карточек можно составить слово «ТЕМА».
ОТВЕТЫ.
12.1 0.0175 12.2а)  б)
б) 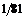 12.3а)
12.3а)  ; б)
; б) 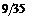 ; в)
; в)  ; г)
; г) 
12.4 а) 0.384 б) 0.096 в) 0.008; г)  . 12.5 а)
. 12.5 а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  12.6а)
12.6а)  ; б)
; б)  ; в)
; в) 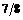 ; г)
; г) 
12.7а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  12.8а)
12.8а) 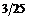 ;б)
;б)  ; в)
; в)  ; г)
; г)  12.9 а)
12.9 а)  ; б)
; б)  12.10
12.10  12.11
12.11  12.12 0.5 12.13
12.12 0.5 12.13  12.14 0.3053 12.15
12.14 0.3053 12.15  12.16 0.0273 12.17 0.354 12.18
12.16 0.0273 12.17 0.354 12.18 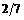 12.19а)
12.19а)  б)
б) 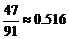 12.20 а)
12.20 а) 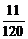 б)
б) 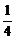 12.21а)
12.21а)  б)
б)  12.22а)
12.22а) 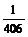 б)
б)  12.23а)
12.23а)  б)
б)  12.24а)
12.24а)  б)
б)  12.25
12.25  12.26
12.26  12.27
12.27