Раздел 5. Дифференциальное исчисление функции одной переменной
Справочный материал по теме
Производная функции
Пусть дана функция 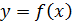 с областью определения D (f).
с областью определения D (f).
Если 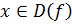 и Δ x ≠ 0 – приращение аргумента, такое, что х + Δ x
и Δ x ≠ 0 – приращение аргумента, такое, что х + Δ x 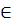
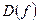
Опр. 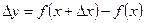 – приращение функции, в точке х, соответствующее приращению аргумента Δ x.
– приращение функции, в точке х, соответствующее приращению аргумента Δ x.
Опр. Производной функции 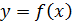 называется предел разностного отношения при Δ x →0, если этот предел существует и конечен.
называется предел разностного отношения при Δ x →0, если этот предел существует и конечен.
 =
= 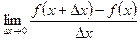 < +∞ – производная функции в точке х => говорят, что
< +∞ – производная функции в точке х => говорят, что 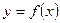 дифференцируема в точке х.
дифференцируема в точке х.
Если  = +∞, то говорят, что существует бесконечная производная функции в точке х.
= +∞, то говорят, что существует бесконечная производная функции в точке х.
Правила дифференцирования
1) 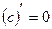 , где с – const
, где с – const
2) 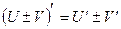
3) 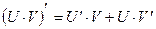
4) 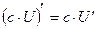 , где с – const
, где с – const
5) 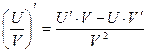 , V ≠ 0
, V ≠ 0
Таблица производных
1.  – степенная функция; 2.
– степенная функция; 2. 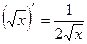
3.  – показательная функция; 4.
– показательная функция; 4. 
5.  ; 6.
; 6. 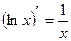
7. 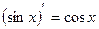 ; 8.
; 8. 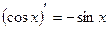
9. 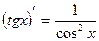 ; 10.
; 10. 
11. 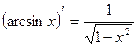 ; 12.
; 12. 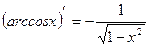
13. 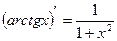 ; 14
; 14 
Производная сложной функции
Правило: Если у = f (z) дифференцируема в точке z, а z = φ (х) дифференцируема в точке х, то у = f (φ (х)) дифференцируема в точке х и 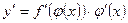 или
или 
Производные высших порядков
Опр. Производная второго порядка (вторая производная) от функции 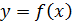 есть производная от её производной:
есть производная от её производной: 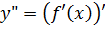 .
.
Опр. Производная третьего порядка (третья производная) от функции 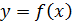 есть производная от её второй производной:
есть производная от её второй производной: 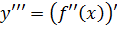 .
.
Опр. Производная n-го порядка (n - я производная) от функции 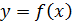 есть производная от её (n – 1)-й производной:
есть производная от её (n – 1)-й производной: 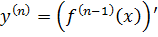 .
.
Производная неявной функции
Если функция 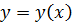 задана уравнением, не разрешенным относительно у, то для нахождения производной у
задана уравнением, не разрешенным относительно у, то для нахождения производной у  надо продифференцировать по х обе части этого уравнения, учитывая, что у есть функция от х, и затем разрешить полученное уравнение относительно у
надо продифференцировать по х обе части этого уравнения, учитывая, что у есть функция от х, и затем разрешить полученное уравнение относительно у  . Чтобы найти у
. Чтобы найти у 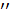 , надо уравнение продифференцировать дважды по х и т. д.
, надо уравнение продифференцировать дважды по х и т. д.
Производная функции, заданной параметрически
Если зависимость функции у от независимой переменной х задана с помощью вспомогательной переменной (параметра) t:

то  ,
,  .
.
Дифференциал функции
Опр. Дифференциалом dy функции 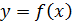 называется главная часть её приращения, пропорциональная приращению Δ x независимой переменной х.
называется главная часть её приращения, пропорциональная приращению Δ x независимой переменной х.
Дифференциал dх независимой переменной х равен её приращению Δ x:
dх = Δ x.
Дифференциал любой дифференцируемой функции 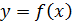 равен произведению её производной на дифференциал независимой переменной:
равен произведению её производной на дифференциал независимой переменной:
dy = 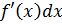 .
.
Если Δ x достаточно мало по абсолютной величине, то с точностью до бесконечно малых более высокого порядка, чем Δ x, имеет место приближенное равенство: Δ у ≈ dy, или 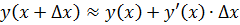 .
.
Раскрытие неопределенностей. Правило Лопиталя
Неопределенности вида 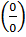 и
и 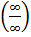 раскрываются по правилу Лопиталя.. Пусть функции
раскрываются по правилу Лопиталя.. Пусть функции 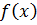 и
и 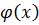 дифференцируемы в некоторой окрестности точки а (за исключением, быть может, её самой), причем
дифференцируемы в некоторой окрестности точки а (за исключением, быть может, её самой), причем 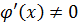 . Тогда если
. Тогда если 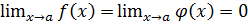 или
или 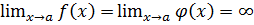 , то
, то 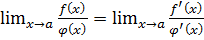 при условии, что предел правой части равенства существует (правило Лопиталя). Это правило применимо и в том случае, когда
при условии, что предел правой части равенства существует (правило Лопиталя). Это правило применимо и в том случае, когда  .
.
Монотонность функции
Опр. Функция называется возрастающей в некотором промежутке, если в этом промежутке каждому большему значению аргумента соответствует большее значение функции.
Опр. Функция называется убывающей в некотором промежутке, если в этом промежутке каждому большему значению аргумента соответствует меньшее значение функции.
Опр. Возрастающие и убывающие функции называются монотонными.
Опр. Функция называется кусочно-монотонной, если её область определения может быть представлена в виде объединения промежутков, на каждом из которых функция монотонна или постоянна.
Монотонность функции 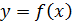 характеризуется знаком её производной, а именно:
характеризуется знаком её производной, а именно:
1)  > 0 на (а; b)
> 0 на (а; b) 
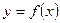 возрастает на (а; b)
возрастает на (а; b)
2)  < 0 на (а; b)
< 0 на (а; b) 
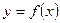 убывает на (а; b)
убывает на (а; b)
Следовательно, отыскание промежутком монотонности функции 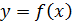 сводится к нахождению промежутков знакопостоянства её первоё производной
сводится к нахождению промежутков знакопостоянства её первоё производной  .
.
Опр. Точка х0 называется точкой максимума функции 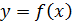 , если существует окрестность точки х0 такая, что для всех х (х ≠ х0) этой окрестности выполняется неравенство:
, если существует окрестность точки х0 такая, что для всех х (х ≠ х0) этой окрестности выполняется неравенство:  .
.
Опр. Точка х0 называется точкой минимума функции 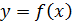 , если существует окрестность точки х0 такая, что для всех х (х ≠ х0) этой окрестности выполняется неравенство:
, если существует окрестность точки х0 такая, что для всех х (х ≠ х0) этой окрестности выполняется неравенство: 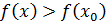 .
.
Опр. Точки максимума и минимума функции называются точками её экстремума, а значение функции в точке максимума (минимума) – максимумом (минимумом) или экстремумом функции.
Точками экстремума могут служить только критические точки 1-го рода, т.е. точки, принадлежащие области определения функции, в которых первая производная  обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.
Точками экстремума являются лишь те из критических точек, при переходе через которые первая производная меняет знак, а именно, если при переходе через критическую точку х = х0 слева направо знак  меняется с плюса на минус (с минуса на плюс), то точка х = х0 есть точка максимума (минимума).
меняется с плюса на минус (с минуса на плюс), то точка х = х0 есть точка максимума (минимума).
В итоге получаем правило отыскания промежутков монотонности и экстремумов функции 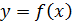 .
.
1. Найти область определения функции 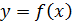 .
.
2. Найти нули и точки разрыва  .
.
3. На числовой прямой отметить найденные точки с учетом области определения функции.
4. Определить знак  в образовавшихся промежутках.
в образовавшихся промежутках.
5. Сделать соответствующие выводы.
Следует отметить, что точки, в которых производная обращается в нуль, иногда проще исследовать на экстремум, выяснив знак второй производной в этих точках 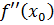 : точка х = х0, в которой
: точка х = х0, в которой  , а
, а 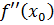 существует и отлична от нуля, является экстремальной, а именно, точкой максимума, если
существует и отлична от нуля, является экстремальной, а именно, точкой максимума, если 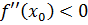 , и точкой минимума, если
, и точкой минимума, если 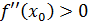 .
.
Направление выпуклости кривой. Точки перегиба.
Опр. Кривая называется выпуклой вверх (вниз) в некотором промежутке, если она расположена ниже (выше) касательной, проведенной к кривой в любой точке этого промежутка.
Направление выпуклости кривой, являющейся графиком функции 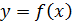 , характеризуется знаком второй производной
, характеризуется знаком второй производной 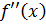 , а именно, если в некотором промежутке
, а именно, если в некотором промежутке  (
(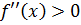 ), то кривая направлена выпуклостью вверх (вниз) в этом промежутке.
), то кривая направлена выпуклостью вверх (вниз) в этом промежутке.
Таким образом, отыскание промежутков направления выпуклости графика функции 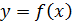 сводится к нахождению промежутков знакопостоянства её второй производной
сводится к нахождению промежутков знакопостоянства её второй производной 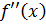 .
.
Опр. Точкой перегиба кривой называется такая её точка, в которой происходит смена направления выпуклости.
Точками перегиба графика функции 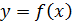 могут служить только точки, абсциссы которых являются критическими точками 2-го рода, т.е. точки, находящиеся внутри области определения функции
могут служить только точки, абсциссы которых являются критическими точками 2-го рода, т.е. точки, находящиеся внутри области определения функции 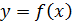 , в которых вторая производная
, в которых вторая производная 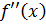 обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.
Точками перегиба графика функции 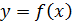 являются лишь те из указанных точек, при переходе через которые вторая производная
являются лишь те из указанных точек, при переходе через которые вторая производная 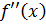 меняет знак.
меняет знак.
Таким образом, получаем правило отыскания промежутков направления выпуклости и точек перегиба функции.
1. Найти область определения функции 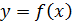 .
.
2. Найти нули и точки разрыва 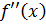 .
.
3. На числовой прямой отметить найденные точки с учетом области определения функции.
4. Определить знак 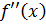 в образовавшихся промежутках.
в образовавшихся промежутках.
5. Сделать соответствующие выводы.