МИНОБРНАУКИ РОССИИ. РЕЗОНАНС НАПРЯЖЕНИЙ

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Юго-Западный государственный университет»

(ЮЗГУ)

Кафедра электроснабжения

 

УТВЕРЖДАЮ

Проректор по учебной работе

__________________________

«_» _________________2014 г.

 

Лабораторный практикум по дисциплине теоретические основы электротехники.

Методические указания по выполнению лабораторной работы для студентов специальностей 140400.62

 

УДК 621. (3.01)

Составители: Л.В.Плесконос

 

 

Рецензент

Кандидат технических наук, доцент А.Л.Овчинников

 

 

Исследование резонанса напряжений в цепи с последовательным соединением индуктивного и емкостного участков: методические указания по выполнению лабораторной работы / Юго.-Зап. гос. ун-т; сост.: Л.В.Плесконос, Курск,2014,__с.: ил. 5,табл. 1, прилож. 2. Библиогр.: с.15.

Содержат сведения по вопросам исследования резонанса напряжений в цепи с последовательным соединением индуктивного и емкостного участков. Указывается порядок выполнения лабораторной работы, подходы к решению различных задач и правила оформления лабораторной работы.

Методические указания соответствуют требованиям программы, утвержденной учебно-методическим объединением по направлению электроэнергетика и электротехника.

Предназначены для студентов специальностей 140400.62

 

Текст печатается в авторской редакции

Подписано в печать. Формат 60х84 1/16

Усл.печ.л. Уч.-изд.л. Тираж 100 эск. Заказ. Бесплатно.

Юго-Западный государственный университет.

305040 г.Курск ул. 50 лет Октября 94.

РЕЗОНАНС НАПРЯЖЕНИЙ

Целью работы является изучение резонанса в цепи с последовательным соединением индуктивного и емкостного участков.

 

СОДЕРЖАНИЕ РАБОТЫ

В работе проводится измерение резонансного и ряда других режимов цепи, состоящей из последовательных катушки индуктивности и батареи конденсаторов с переменной емкостью. По данным измерений выполняются расчет и построение резонансных кривых и векторных диаграмм.

 

1. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

 

Резонансом называют явление резкого увеличение тока или напряжения в электрической цепи, содержащей участки индуктивного и ёмкостного характера, при котором разность фаз напряжения и тока на входе цепи равна нулю

ϕ = 0. (1)

Для режима резонанса в цепи, представляющей последовательное соединение индуктивной катушки и конденсатора (рис. 1.1) характерна возможность возникновения напряжений на индуктивности и емкости, равных по модулю и превышающих приложенное напряжение (отсюда и название – резонанс напряжений). Кроме общего условия (1) для резонанса напряжений справедливо

Im { Z вх} = 0, (2)

т. е. X = X_L – X_C = 0.

 

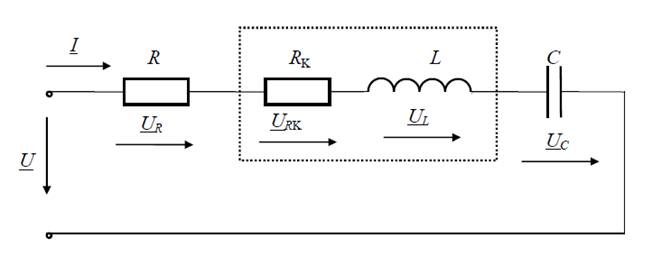Для реальной электрической цепи (рис. 1.1)

 

Рис. 1.1 Электрическая схема резонансной цепи.

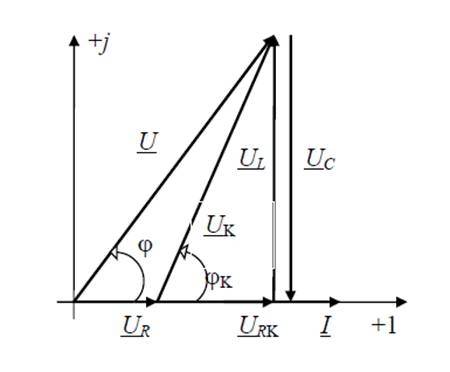векторная диаграмма в режиме резонанса напряжений имеет вид, изображенный на (рис.1.2).

 

 

Рис. 1.2 Векторная диаграмма напряжений в точке резонанса

Из условия резонанса напряжений (2) следует, что в режиме резонанса индуктивное сопротивление цепи равно емкостному |X_L| = |X_C|

Ѡ₀ L = 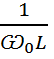. (3)

На (рис. 1.3) показаны резонансные кривые последовательного контура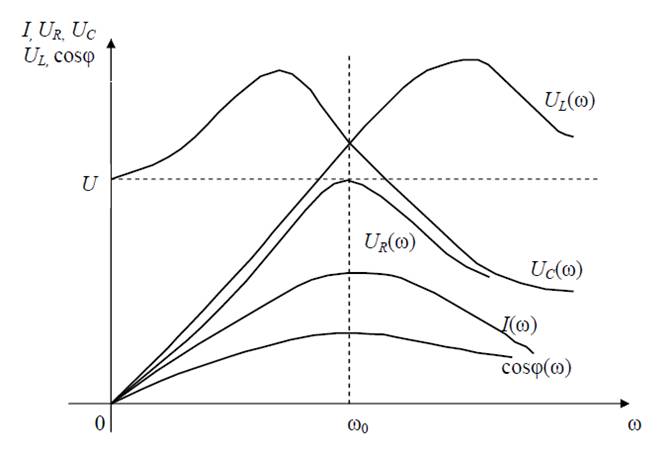

 

 

Рис. 1.3 Зависимость напряжения, тока, cosϕ от частоты Ѡ последовательной R, L, C цепи.

Следовательно, режим резонанса напряжений можно установить подбором любого из параметров цепи L, C или Ѡ из условия (3)

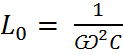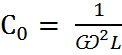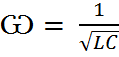; ; . (4)

Полная мощность цепи

S = UI =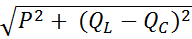

при резонансе имеет активный характер, а реактивные емкостная и индуктивная мощности равны между собой

Q_L = I²X_L; Q_C = I²X_C;

|Q_L| = |Q_C|.

Частота, при которой наступает резонанс напряжений, определяется из условия резонанса (x=0):

Ѡ₀ = .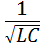

Резонансные значения индуктивного сопротивления Ѡ₀L или емкостного сопротивления (1/ Ѡ₀С), как видно также из условия резонанса, равны 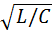. Величину ρ = 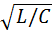называют характеристическим (или волновым) сопротивлением контура.

 

Резонансное напряжение индуктивности U _Lрез (для катушки – реактивная составляющая напряжения U_K) и резонансное напряжение конденсатора U _Cрез выражается в виде

U _Lрез = Ѡ₀LI _рез = ρ = QU,

U _Cрез = (1/Ѡ₀C) I _рез = ρ = QU,

где Q – добротность контура, - величина, характеризующая резонансные цепи.

Из этих формул

Q = = ,

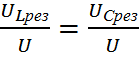т. е. добротность показывает, во сколько раз напряжение катушки или конденсатора может быть больше, чем напряжение на зажимах цепи.

Величина d, обратная добротности, называется затуханием контура:

d = .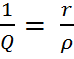

Понятия добротности и затухания применяются для характеристики резонансных цепей (колебательных контуров), широко используемых в радиотехнике.

В электроэнергетике могут возникать непредусмотренные условия, когда система попадает в режим, близкий к резонансу. Например, при обрыве линии передачи, питающей ненагруженный трансформатор (рис. 1.4), может случиться резонанс между емкостью

,

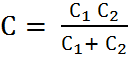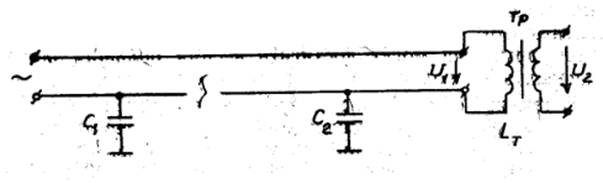где С₁ и С₂ – емкости на землю двух участков линии, индуктивностью L первичной обмотки трансформатора.

 

Рис. 1.4 Пример возникновения условий резонанса.

Активные сопротивления в таких системах малы, и поэтому резонансный ток, а следовательно, и напряжения на обмотках трансформатора могут достигать весьма больших значений, опасных для изоляции электрической установки.

В технике слабых токов, наоборот, часто желательным является наибольшее повышение напряжений реактивных элементов. С этой целью добротность колебательных контуров, применяемых, например, в радиотехнике, повышают до трехсот и более.

Поведение цепи при постоянном приложенном напряжении и изменении любой из величин, от которых зависит наступление резонанса, характеризуют резонансные кривые. Это зависимости от L, C или Ѡ параметров цепи z, ϕ, r, x, y, g и b; а также «режимных» величин I, U_L, U_С и др. На практике наибольший интерес представляют частотные характеристики, – зависимости от частоты (рис. 1.5).

 

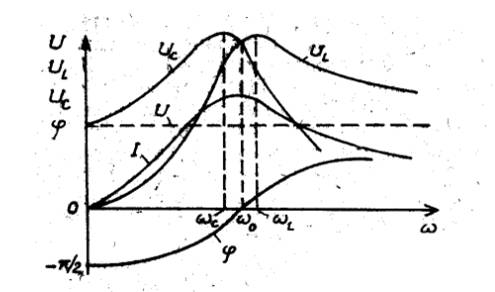
Рис. 1.5 Резонансные кривые.

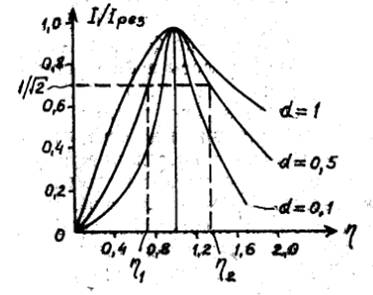Для удобства сравнения различных резонансных контуров переходят к резонансным кривым в относительных единицах. К примеру, на рис. 1.6 приведено семейство кривых (I / I _рез) = F (η), где η = Ѡ/Ѡ₀.

 

Рис. 1.6 Голоса пропускания контура.

Оказывается, форма таких кривых, («острота резонансных кривых») зависит только от добротности Q (или затухания d).

Удобной характеристикой кривых (а заодно и колебательного контура) является ширина резонансной кривой или полоса пропускания контура, определяемая как ∆η = η₂ – η₁, где η₁ = Ѡ₁/ Ѡ₀ и η₂ = Ѡ₂/ Ѡ₀ – значения относительных частот, при которых ток в цепи в 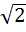раз меньше, чем I _рез. Можно показать, что при этом ∆η = d = 1/Q. Следовательно, при известных добротности контура Q и резонансной частоте Ѡ₀ определяются и границы полосы пропускания Ѡ₁ = Ѡ₀ η₁ и Ѡ₂ = Ѡ₀ η₂.

При энергетическом рассмотрении оказывается, что в режиме резонанса суммарная энергия, запасенная в электрическом и магнитном полях цепи, - величина постоянная. Это означает, что если в магнитном поле катушки энергия уменьшается, то на столько же она возрастает в электрическом поле конденсатора. Происходят колебания энергии между индуктивностью и емкостью, и такой обмен является причиной повышенных напряжений реактивных элементов. Энергия, поступающая из сети, поскольку ϕ = 0, целиком поглощается активным сопротивлением r.

 

2. ЗАДАНИЕ

Предварительные замечания

 

Схема рабочей цепи приведена на рис. 2.1.

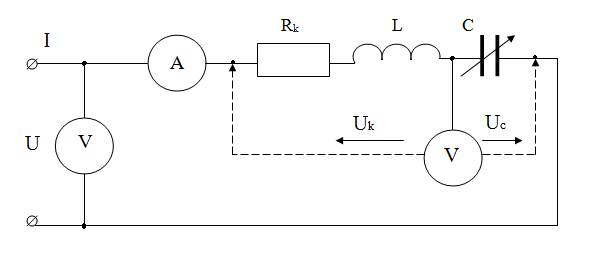
Рис. 2.1 Схема рабочей цепи.

Источником питания является ЛАТР, подключаемый к сети 50 Гц. Характеристики используемых элементов стенда и приборов и рекомендуемый диапазон напряжений питания указаны в приложении. Установленное в начале работы напряжение поддерживается постоянным до окончания всех опытов.

Выполнить следующее:

1. Собрать рабочую цепь.

2. Снять резонансные кривые при изменении емкости. Опыты провести при неизменном напряжении на зажимах цепи, изменяя емкость от нуля до предельного значения, причем вблизи резонанса – через малые ступени (см. Приложение). Данные опытов внести в таблицу 1.

 

 

f = 50 Гц, U = Таблица 1

№ п. п.	1 2 3....	Примечание
Из опытов	С, мкФ I, A UК, В UC, В
Из расчетов	Z, Ом ZK, Ом R, Ом XL, Ом XС, Ом X, Ом ϕ, град Uа, В UL, В Q		U/I UK/I U/Iрез 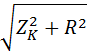UC/I XL – XC arctg(X/R) RI XLI ULрез/Uвх

 

3. ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТОВ

3. По результатам измерений найти значения всех расчетных величин таблицы 1.

4. Начертить на одном общем графике линию 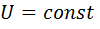и резонансные кривые 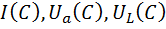и 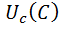, на другом – кривые 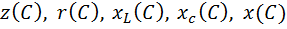и .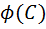

5. Построить (с указанием масштабов) векторные диаграммы для случаев .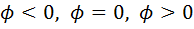

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Чем отличается цепь (или часть цепи), в которой возможен резонанс напряжений? Каковы условие и признаки этого режима?

2. Какими способами достигается режим резонанса? Как установить по приборам, что в цепи имеет место резонанс?

3. Изменится ли условие резонанса, если параллельно катушке или конденсатору подключить резистор?

4. Каким образом в условиях рабочей цепи (рис. 6) можно измерить индуктивность катушки?

5. Начертите резонансные кривые r(Ѡ), x_L(Ѡ), x_C (Ѡ), x(Ѡ), z (Ѡ), ϕ (Ѡ), I (Ѡ), U_L(Ѡ) и U_C(Ѡ). Дайте им объяснение на основе соответствующих алгебраических выражений.

6. Поясните смысл понятий добротности, затухания и полосы пропускания резонансных контуров.

 

ЛИТЕРАТУРА

1. Бессонов Л. А. Теоретические основы электротехники (электрические цепи). М., «Высшая школа», 1978, с.88 – 90.

2. Зевеке Г. В., Ионкин П. А., Нетушил А. В., Страхов С. В. Основы теории цепей. «Энергия», 1965, §§7-4 – 7-6, 9-1 – 9-3.

Приложение к работе

Значения r и L в схеме рабочей цепи (рис. 6) представляют параметры катушки индуктивности L₁ стенда. Изменение емкости С осуществляется подключением или отключением параллельного конденсатора батареи. Рекомендуемый ряд значений общей емкости батареи для различных пар присоединяемых выводов катушки, а также соответствующие пределы выбора напряжения питания цепи даны в таблице.

Выводы	1 – 3	1 – 4	2 – 3	2 – 4
Напряжение питания, В	50 – 70	50 – 70	50 – 60	55 – 70
№ опыта	С, мкф	С, мкф	С, мкф	С, мкф
	14,5	5,25		7,5
		5,5
	15,5			8,5
		6,5
	16,5			9,5

 

Измерительные приборы:

— амперметр электромагнитный класса 0,5 на I А (типа Э514) — 1 шт;

— вольтметры электромагнитные класса 0,5 на 150 и 300 В (типа Э515) — 3 шт.