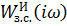Параметры объекта заданы в виде передаточной функции
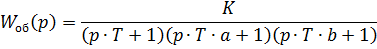
Исходные данные (табл.1).
Таблица 1
| № в журнале, Т, с | К | a | b | № в журнале, Т, с | К | а | b |
| 1,8 | 1,5 | 1,3 | 1,7 | ||||
| 1,2 | 0,9 | 1,4 | 1,6 | ||||
| 1,5 | 1,2 | 1,5 | 1,3 | ||||
| 0,3 | 0,5 | 1,6 | 1,2 | ||||
| 1,1 | 0,7 | 1,7 | 1,1 | ||||
| 1,4 | 0,8 | 1,8 | 0,9 | ||||
| 1,6 | 0,9 | 1,3 | 0,8 | ||||
| 3,5 | 0,4 | 0,6 | 1,2 | 0,7 | |||
| 3,5 | 0,5 | 0,7 | 1,1 | 0,6 | |||
| 3,5 | 0,2 | 0,8 | 0,9 | 0,7 | |||
| 3,5 | 0,3 | 0,6 | 3,5 | 0,8 | 0,6 | ||
| 3,5 | 1,3 | 0,2 | 3,5 | 0,7 | 0,5 | ||
| 3,5 | 1,2 | 0,4 | 3,5 | 0,6 | 0,4 | ||
| 1,1 | 0,6 | 3,5 | 0,5 | 0,3 | |||
| 0,9 | 0,7 | 3,5 | 0,4 | 0,8 | |||
| 0,8 | 0,9 | 3,5 | 0,3 | 0,9 | |||
| 0,7 | 0,5 | 3,5 | 0,5 | 1,1 | |||
| 1,7 | 0,3 | 3,5 | 0,2 | 1,2 | |||
| 0,7 | 1,1 | 3,5 | 0,8 | 0,7 | |||
| 0,6 | 0,9 | 3,5 | 0,2 | 0,4 | |||
Далее приведен один из возможных вариантов расчета с исходными данными:
| Т, с | К | a | b |
| 0,8 | 1,1 |
Последовательность проводимых вычислений:
1. Расчет и построение графиков 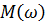 ,
, 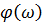 ,
, 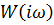 для объекта с заданной передаточной функцией Wоб(p).
для объекта с заданной передаточной функцией Wоб(p).
Данную передаточную функцию можно рассмотреть как последовательное соединение трех инерционных звеньев с передаточными функциями:
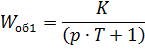
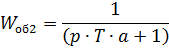
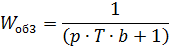
Рассмотрим первое инерционное звено: 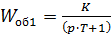 .
.
Для определения зависимости от частоты фазы и амплитуды произведем замену 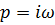 ,получим:
,получим:
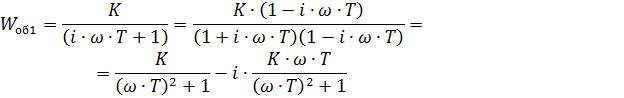
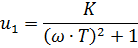
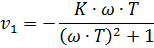
Амплитуда (коэффициент передачи звена):
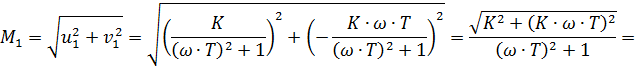
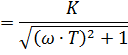
Фазовый сдвиг выходного сигнала:
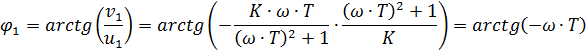
Рассмотрим второе инерционное звено: 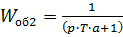 .
.
Для определения фазы и амплитуды произведем замену 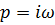 ,получим:
,получим:
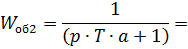
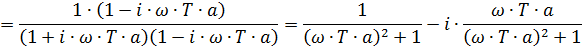
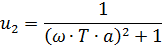
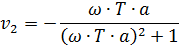
Амплитуда:
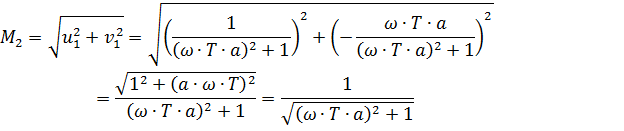
Фаза:
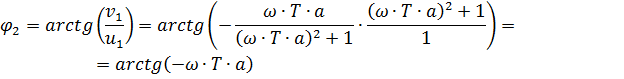
Рассмотрим третье инерционное звено: 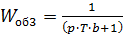 .
.
Для определения фазы и амплитуды произведем замену 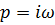 ,получим:
,получим:
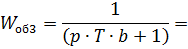
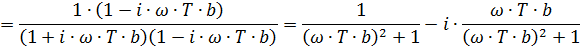
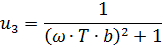
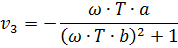
Амплитуда:
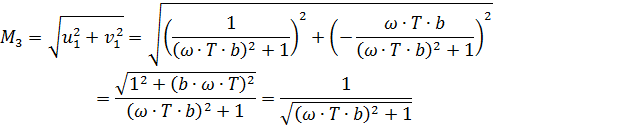
Фаза:
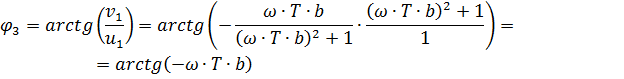
При последовательном соединении:
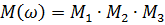
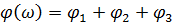
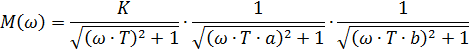
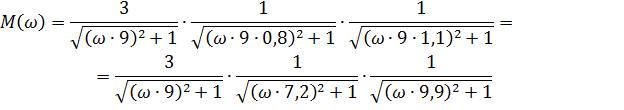
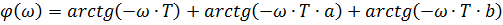
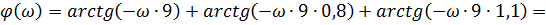
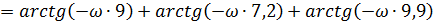
Общая функция для построения комплексной частотной характеристики:
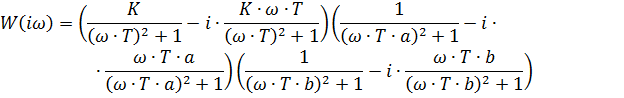
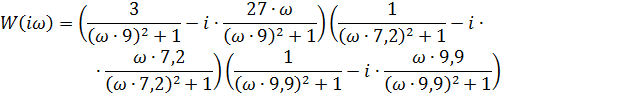
Строим три полученные функции в программе Maple. Сведем значения 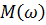 ,
, 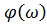 ,
, 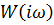 (табл.2).
(табл.2).
Таблица 2

| 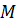
| 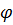
| 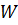
|
| 0,0 | 3,0 | 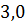
| |
| 0,01 | 2,96571 | -0,26031 | 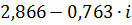
|
| 0,02 | 2,86675 | -0,51658 | 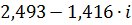
|
| 0,03 | 2,71384 | -0,76515 | 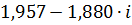
|
| 0,04 | 2,52188 | -1,00302 | 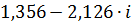
|
| 0,05 | 2,30689 | -1,22805 | 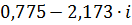
|
| 0,06 | 2,08343 | -1,43891 | 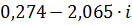
|
| 0,07 | 1,86303 | -1,63504 | 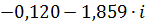
|
| 0,08 | 1,65380 | -1,81645 | 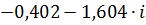
|
| 0,09 | 1,46067 | -1,98350 | 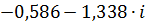
|
| 0,1 | 1,28601 | -2,13721 | 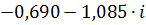
|
| 0,11 | 1,13030 | -2,27819 | 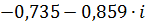
|
| 0,12 | 0,99320 | -2,40752 | 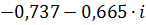
|
| 0,13 | 0,87312 | -2,52617 | 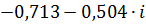
|
| 0,14 | 0,76852 | -2,63511 | 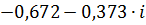
|
| 0,15 | 0,67765 | -2,73523 | 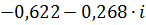
|
| 0,16 | 0,59882 | -2,82739 | 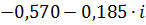
|
| 0,17 | 0,53044 | -2,91235 | 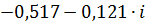
|
| 0,18 | 0,47110 | -2,99079 | 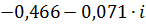
|
| 0,19 | 0,41953 | -3,06337 | 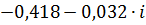
|
| 0,2 | 0,37464 | -3,13062 | 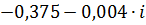
|
| 0,21 | 0,33548 | -3,19307 | 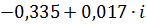
|
| 0,3 | 0,13968 | -3,59932 | 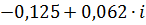
|
| 0,4 | 0,06448 | -3,85989 | 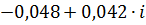
|
| 0,5 | 0,03449 | -4,02344 | 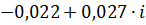
|
| 0,6 | 0,20452 | -4,13502 | 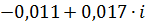
|
| 0,7 | 0,01307 | -4,21579 | 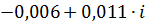
|
| 0,8 | 0,00884 | -4,27688 | 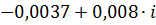
|
| 0,9 | 0,00625 | -4,32467 | 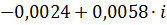
|
| 1,0 | 0,00458 | -4,36306 | 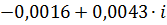
|
| 2,0 | 0,00058 | -4,53709 | 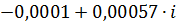
|
Амплитудно-частотная характеристика 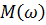 , (рис.1)
, (рис.1)
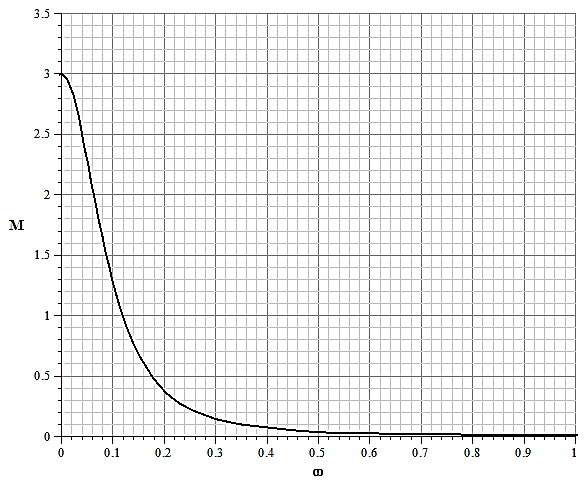
Рис. 1
Фазо-частотная характеристика 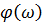 ,(рис.2)
,(рис.2)
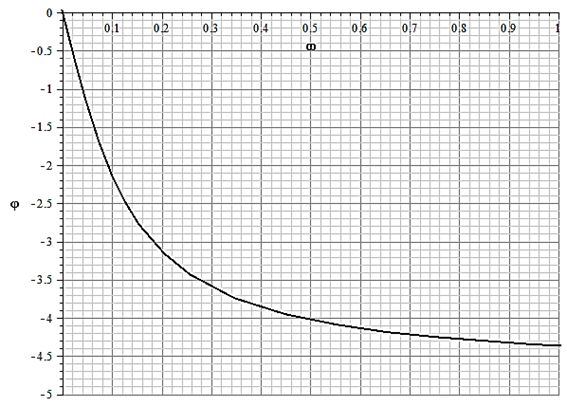
Рис.2
Комплексная частотная характеристика (амплитудно-фазовая характеристика или годограф) 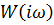 ,(рис.3)
,(рис.3)
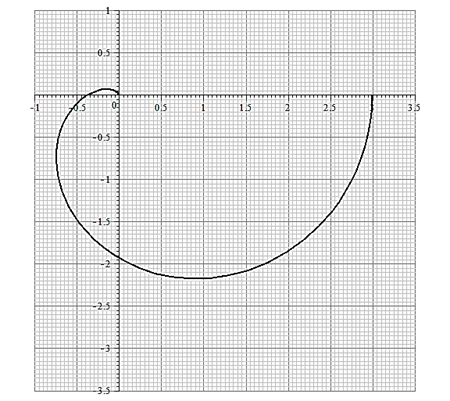
Рис. 3
2. Определение критических значений частот 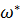 для П-регулятора и И-регулятора из условия, что
для П-регулятора и И-регулятора из условия, что 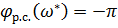 (т.е. суммарный фазовый сдвиг объекта и последовательно включенного регулятора равен -180°).
(т.е. суммарный фазовый сдвиг объекта и последовательно включенного регулятора равен -180°).
Выполнить аналитическим способом с применением интерполяции и по графику 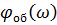 .
.
Критическая частота – частота, при которой в системе возникают незатухающие колебания. Это происходит в случае, если суммарный сдвиг фаз в системе объект-регулятор составляет 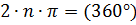 .
.
Т.к. П - регулятор дает сдвиг фаз в 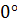 ,
, 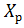 дает сдвиг в
дает сдвиг в 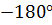 (т.к. обратная связь в АСР отрицательная), следовательно,
(т.к. обратная связь в АСР отрицательная), следовательно, 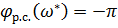 . (чтобы в сумме было
. (чтобы в сумме было 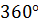 ).
).
Из таблицы значений:
| ω | φ |
| 0,20 | -3,13062 |
| 0,21 | -3,19307 |
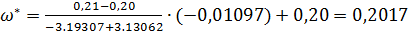 рад/с.
рад/с.
Тогда 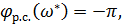 при частоте
при частоте 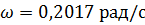 .
.
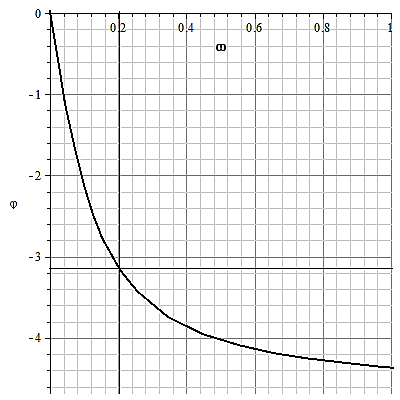
Рис.4. Критическая частота для П-регулятора.
Т.к. И - регулятор дает сдвиг фаз в 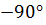 ,
, 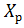 дает сдвиг в
дает сдвиг в 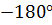 , следовательно
, следовательно 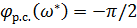 . (чтобы в сумме было
. (чтобы в сумме было 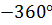 ).
).
Из таблицы значений:
| ω | φ |
| 0,06 | -1,43891 |
| 0,07 | -1,63504 |
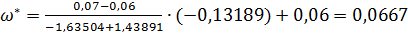 рад/с.
рад/с.
Тогда 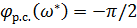 при частоте
при частоте 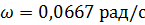 .
.
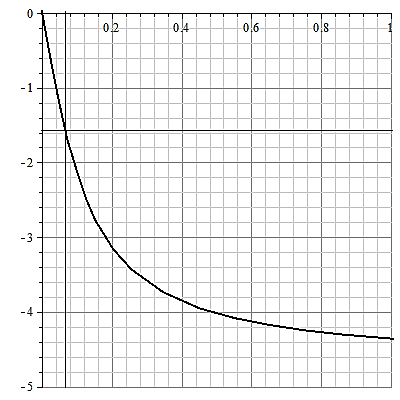
Рис.5. Критическая частота для И-регулятора.
Сравнивая два метода нахождения критической частоты 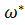 для П и И-регуляторов, а именно, метод интерполяции и графический метод, видим, что полученные результаты практически совпадают, т. е. методы имеют почти одинаковую точность.
для П и И-регуляторов, а именно, метод интерполяции и графический метод, видим, что полученные результаты практически совпадают, т. е. методы имеют почти одинаковую точность.
3. Определение критических значений параметров 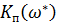 и
и 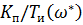 для системы с П-регулятором и системы с И-регулятором, при которых система выходит на границу устойчивости. Это условие (баланс амплитуд)
для системы с П-регулятором и системы с И-регулятором, при которых система выходит на границу устойчивости. Это условие (баланс амплитуд)
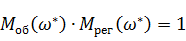
· П – регулятор

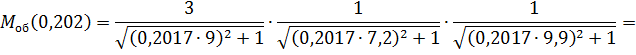
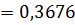
Тогда 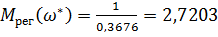
Для П-регулятора 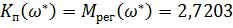
· И-регулятор
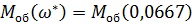
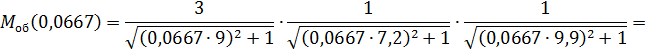
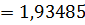
Тогда 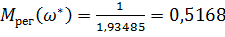
Для И-регулятора:
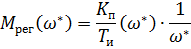
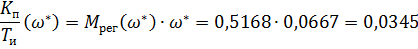
| П – регулятор | 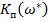
| 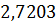
|
| И–регулятор | 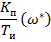
| 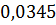
|
4. Вычисление оптимальных (рабочих) параметров для П-регулятора и И-регулятора 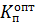 и
и 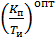 из условия:
из условия:
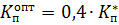
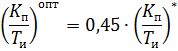
· П – регулятор
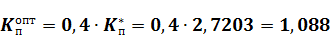
· И–регулятор
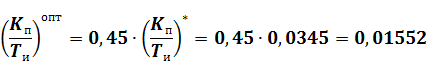
5. Расчет и построение 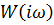 для разомкнутой и замкнутой системы по каналу управления
для разомкнутой и замкнутой системы по каналу управления 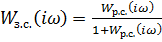 . На графиках отметить 5-7 частот и выделить резонансную частоту
. На графиках отметить 5-7 частот и выделить резонансную частоту 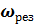 . ( В приводимом примере это не сделано!)
. ( В приводимом примере это не сделано!)
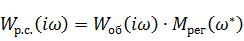
· П-регулятор
Т.к. 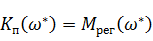 , то
, то 
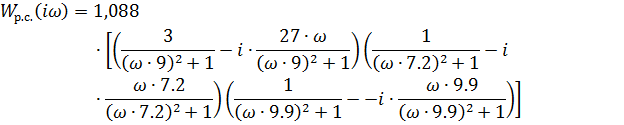
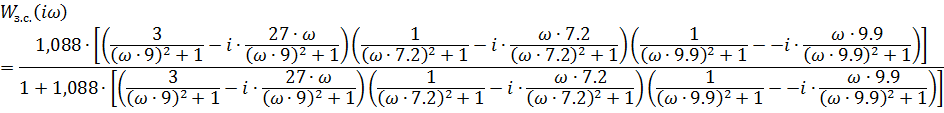
Составим таблицы для 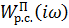 и
и 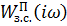 (табл.3)
(табл.3)
Таблица 3

| 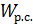
| 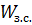
|
| 0,0 | 3,264 | 0,7655 |
| 0,01 | 3,118 – 0,8305∙i | 0,7666 – 0,0471∙i |
| 0,02 | 2,712 – 1,5405∙i | 0,7702 – 0,0954∙i |
| 0,03 | 2,1297 – 2,0451∙i | 0,7761 – 0,1463∙i |
| 0,04 | 1,4755 – 2,3133∙i | 0,7844 – 0,2015∙i |
| 0,05 | 0,8435 – 2,3639∙i | 0,7949 – 0,263∙i |
| 0,06 | 0,2981 – 2,2471∙i | 0,8072 – 0,3337∙i |
| 0,07 | −0,1301 – 2,0228∙i | 0,8206 – 0,4172∙i |
| 0,08 | −0,4376 – 1,7453∙i | 0,8327 – 0,5191∙i |
| 0,09 | –0,6376 – 1,4557∙i | 0,8389 – 0,6468∙i |
| 0,1 | –0,7508 – 1,1807∙i | 0,8289 – 0,8108∙i |
| 0,11 | –0,7992 – 0,9348∙i | 0,7804 – 1,0226∙i |
| 0,12 | –0,8023 – 0,7239∙i | 0,6489 – 1,2855∙i |
| 0,13 | –0,7757 – 0,5484∙i | 0,3610 – 1,5621∙i |
| 0,14 | –0,7312 – 0,4056∙i | –0,1353 – 1,7130∙i |
| 0,15 | –0,6772 – 0,2914∙i | –0,7068 – 1,5411∙i |
| 0,16 | –0,6196 – 0,2014∙i | –1,0535 – 1,0870∙i |
| 0,17 | –0,5620 – 0,1311∙i | –1,0953 – 0,6274∙i |
| 0,18 | –0,5067 – 0,0770∙i | –0,9791 – 0,3089∙i |
| 0,19 | –0,4551 – 0,0357∙i | –0,8272 – 0,1196∙i |
| 0,2 | –0,4076 – 0,0045∙i | –0,6879 – 0,0127∙i |
| 0,4 | –0,0528+0,0462∙i | –0,0533 – 0,0513∙i |
| 0,6 | –0,0121+ 0,0186∙i | –0,0119+ 0,0191∙i |
| 0,8 | –0,0041+ 0,0087∙i | –0,0040+ 0,0088∙i |
| 1,0 | –0,0017+ 0,0047∙i | –0,0017+ 0,0047∙i |
Комплексная частотная характеристика 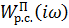 разомкнутой системы с П-регулятором представлена на рисунке 6.
разомкнутой системы с П-регулятором представлена на рисунке 6.
Определим резонансную частоту из графика:
 при
при 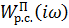 =
=
Пример определения резонансной частоты по КЧХ разомкнутой системы приведен на рис. 4.12 вышеупомянутой книги.
Рис. 6. 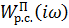
Комплексная частотная характеристика 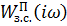 замкнутой системы с П-регулятором представлена на рисунке 7.
замкнутой системы с П-регулятором представлена на рисунке 7.
Определим резонансную частоту из графика:
 при
при 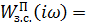
Из нижней формулы на стр. 112 и рис. 4.12б следует, что резонансная частота на КЧХ замкнутой системы соответствует максимальной длине вектора КЧХ.
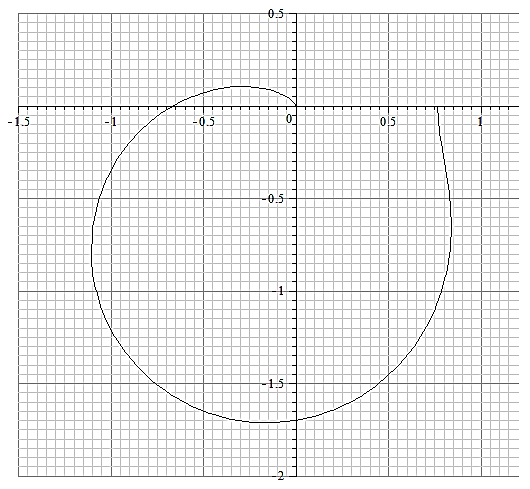
Рис. 7. 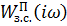
· И-регулятор
Т.к. 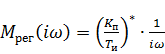 , то получаем
, то получаем
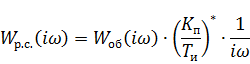
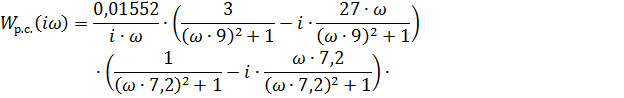
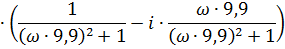
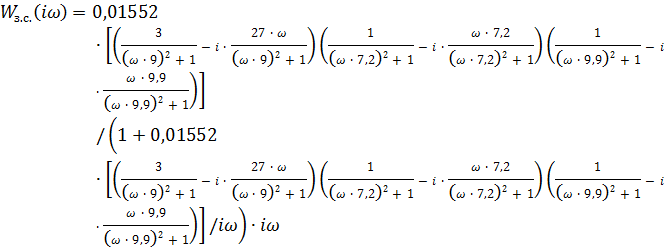
Составим таблицы для 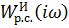 и
и 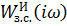 (табл.4)
(табл.4)
Таблица 4

| 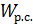
| 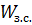
|
| 0,01 | 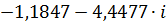
| 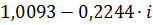
|
| 0,02 | 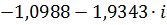
| 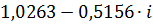
|
| 0,03 | 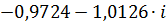
| 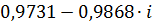
|
| 0,04 | 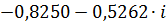
| 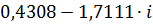
|
| 0,05 | 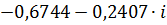
| 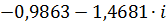
|
| 0,06 | 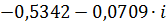
| 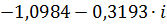
|
| 0,07 | 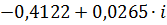
| 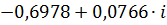
|
| 0,08 | 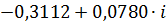
| 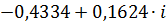
|
| 0,09 | 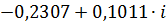
| 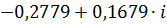
|
| 0,1 | 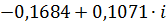
| 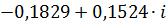
|
| 0,11 | 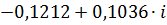
| 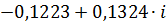
|
| 0,12 | 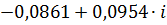
| 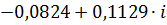
|
| 0,13 | 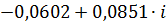
| 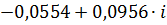
|
| 0,14 | 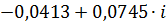
| 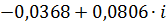
|
| 0,15 | 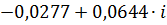
| 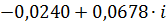
|
| 0,16 | 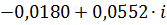
| 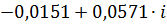
|
| 0,17 | 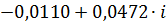
| 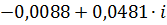
|
| 0,18 | 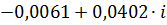
| 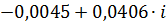
|
| 0,19 | 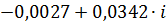
| 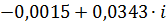
|
| 0,2 | 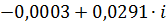
| 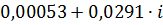
|
| 0,4 | 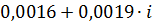
| 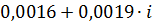
|
| 0,6 | 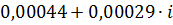
| 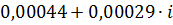
|
| 0,8 | 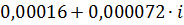
| 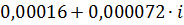
|
| 1,0 | 
| 
|
Комплексная частотная характеристика 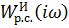 разомкнутой системы с И-регулятором представлена на рисунке 8.
разомкнутой системы с И-регулятором представлена на рисунке 8.
Определим резонансную частоту из графика:
 при
при 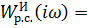
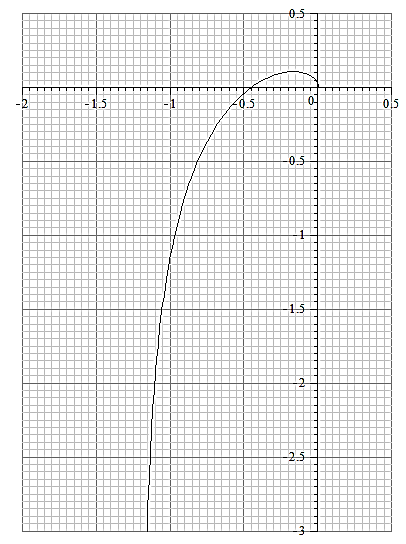
Рис. 8. 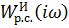
Комплексная частотная характеристика 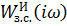 замкнутой системы с И-регулятором представлена на рисунке 9.
замкнутой системы с И-регулятором представлена на рисунке 9.
Определим резонансную частоту из графика:
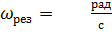 при
при 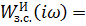
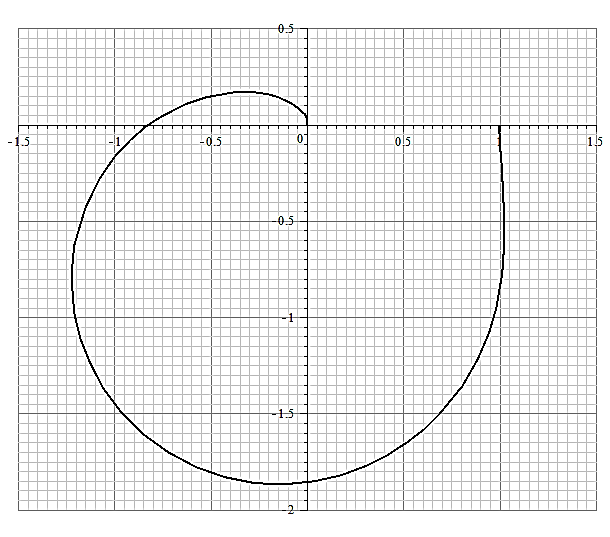
Рис. 9.