Чтобы построить границы области изменения переменных, преобразуем все неравенства в равенства, пронумеруем их и выразим 𝑥2 как функцию 𝑥1
1) 2𝑥1+3𝑥2=60;
x2 = 20-(2/3)*x1;
2) 𝑥1≤18;
x2≤18;
Целевая функция при различных значениях переменных равна некоторой константе С
4) 5*𝑥1+7*𝑥2 =C,
𝑥2=C1−(5/7)∗𝑥1,
где обозначено С1=С/7.
Направление максимального роста целевой функции f задает её вектор градиент. Градиент – это вектор, компоненты которого являются частными производными функции f по 𝑥1 и 𝑥2:
𝛁𝐟= 𝒈𝒓𝒂𝒅⃗(f) = 𝒊 ⃗*𝜕𝑓𝜕𝑋1+ 𝒋⃗ *𝜕𝑓𝜕𝑋2 = 𝒊⃗*5 +𝒋⃗*7
в рассматриваемом случае компоненты градиента равны коэффициентам при 𝑥1 и 𝑥2 в целевой функции, поскольку 𝜕𝑓𝜕𝑋1= 5 и 𝜕𝑓𝜕𝑋2 =7.
Вектор градиента функции f направлен вдоль прямой y = 
x1 перпендикулярно линии функции (перпендикулярно прямой 5*𝑥1+7*𝑥2=C) и указывает направление максимального роста функции f.
Построим графики границ для области изменения переменных, вектор градиента и несколько линий целевой функции для разных значений С1.
Составим команды в кодах МАТЛАБА
x21=20-2*x1/3;
plot(x1,x21,'b','LineWidth',2);
hold on;
plot(x1,x21-x21,'r','LineWidth',2);
ylim([0 20]);
axis equal;
xlim([0 30]);
grid minor;
fplot(@(x1)7*x1/5,[0 100],'k','LineWidth',2.5);
gtext('градиент');
Val=[3 7 15];
f={'f1','f2','f3'};
for i=1:3;
C1=Val(i);
fplot(@(x1)C1-5*x1/7,'g');
gtext(f{i});
end
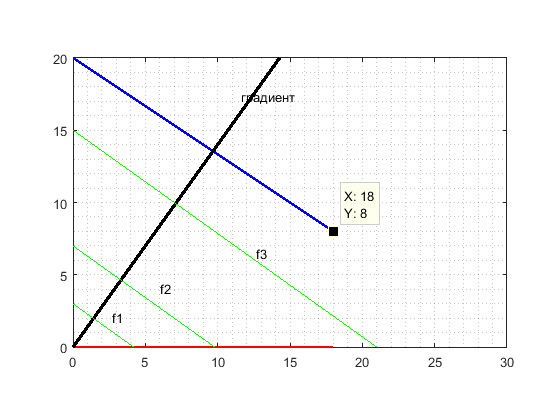
Ответ: 18 шт 5-ти тонных и 8 шт 7-тонных вагонов.
Задача 5:
При изготовлении изделий А, Б, В и С фабрика расходует в качестве сырья сталь и цветные металлы, имеющиеся в ограниченном количестве. Указанные изделия производят с помощью токарных и фрезерых станков. Определить план выпуска продукции, при котором будет достигнута максимальная прибыль. Необходимые данные приведены в таблице.
| Вид ресурса | Объем расхода на одно изделие | Ограничение по объемам ресурсов | |||
| А | Б | В | С | ||
| Сталь, кг | |||||
| Цветные металлы, кг | |||||
| Токарные станки, станко-час | |||||
| Фрезерные станки, станко-час | |||||
| Прибыль, ден. ед. |
Решение:
Пусть x1 – количество изделий А, х2 – количество изделий Б, х3-количество изделий В,х4-количество изделий С.
𝑓(𝑥)=4𝑥1+2𝑥2+4х3+3х4. –прибыль. Нам нужно, чтобы она была максимальная. Значит f(x) – целевая функция.
Получаем:
10𝑥1+20𝑥2+15х3+18х4≤250
0х1+5х2+8х3+7х4≤40
15𝑥1+18х2+12х3+20х4≤100
8х1+12х2+11х3+10х4≤80
И по условию 𝑥1>0,𝑥2>0,х3>0,𝑥4>0
Для решения задачи воспользуемся решателем MATLAB linprog(f,A,b), который по умолчанию отыскивает минимум целевой функции f, поэтому для поиска максимума функции, нужно знак ее коэффициентов изменить на противоположный.
x1=0:0.1:18;
f=[-4 -2 -4 -3];
A=[10 20 15 18;0 5 8 7;15 18 12 20;8 12 11 10];
b=[250 40 100 80];
lb=[0;0;0;0];
ub=[];
Aeq=[];
beq=[];
x = linprog(f,A,b,Aeq,beq,lb,ub)
x =
2.6667 (округляем до целого числа - 2)
5.0000
Ответ: 2 изделия А, 5 изделий В.
Задача 6:
Фирма "Компьютер-сервис" поставляет компьютеры под ключ четырех базовых комплектаций: «домашний»,«игровой», «офисный» и «экстрим». Известны средние затраты времени на сборку, проверку и подключение компьютеров. Каждый компьютер приносит определенный уровень прибыли, но спрос ограничен. Кроме того, в плановом периоде ограничен ресурс человеко-часов, отведенных на выполнение каждой производственной операции. Определить, сколько компьютеров каждого типа необходимо произвести в плановом периоде, имея целью максимизировать прибыль.
| Компьютер | Прибыль за модель У.е. | Максимальный спрос на товар | Требуется часов на подключение | Требуется часов на сборку | Требуется часов на проверку |
| Домашний | 0,9 | 1,2 | 1,3 | ||
| Игровой | 1,1 | 1,5 | 1,5 | ||
| Офисный | 0,7 | 0,9 | 0,9 | ||
| Экстрим | 1,3 | 1,1 | 1,2 | ||
| Доступно человеко-часов на каждую операцию |
Решение:
Пусть x1 – количество домашних компьютеров, х2 – количество игровых компьютеров, х3-количество офисных компьютеров, х4-количество компьютеров экстрим.
𝑓(𝑥)=33𝑥1+39𝑥2+36х3+43х4. –прибыль. Нам нужно, чтобы она была максимальная. Значит f(x) – целевая функция.
Из ограничений:
0.9𝑥1+1.1𝑥2+0.7х3+1.3х4≤70
1.2х1+1.5х2+0.9х3+1.1х4≤55
1.3𝑥1+1.5х2+0.9х3+1.2х4≤35
И по условию 0<𝑥1<87,0<𝑥2<67,0<х3<110,0<𝑥4<45
Для решения задачи воспользуемся решателем MATLAB linprog(f,A,b), который по умолчанию отыскивает минимум целевой функции f, поэтому для поиска максимума функции, нужно знак ее коэффициентов изменить на противоположный.
f=[-33 -39 -36 -43];
A=[0.9 1.1 0.7 1.3;1.2 1.5 0.9 1.1;1.3 1.5 0.9 1.2];
b=[70 55 35];
lb=[0;0;0;0];
ub=[87;67;110;45];
Aeq=[];
beq=[];
x = linprog(f,A,b,Aeq,beq,lb,ub)
x =
38.8889
Так как числа должны быть целыми, то х3=38.
Ответ: 38 офисных компьютеров.