Линейное программирование.
Задача 1: f(x) = 3x1 + x2 + 2x3 → min,
x1 + x2 + x3 ≥1,
2x1 + x2 − x3 ≥−1,
x1 − x2 + x3 = 0,
0≤ x1≤ 1,
0 ≤ x2 ≤ 1,
0≤ x3 ≤ 1.
Решение.
Для решения задачи воспользуемся решателем MATLAB linprog(f,A,b), который по умолчанию отыскивает минимум целевой функции f.
Целевая функция: f(x) = 3x1 + x2 + 2x3.
f=[3 1 2]; %задаем матрицу целевой функции
A=[-1 -1 -1;-2 -1 1]; %задаем матрицу коэффициентов неравенств. При этом неравенства должны быть приведены к виду «меньше или равно»
b=[-1;1]; %задаем матрицу правой части неравенства
lb=[0;0;0]; %задаем матрицу нижних ограничений
ub=[1;1;1]; %задаем матрицу верхних ограничений
Aeq=[1 -1 1]; %задаем матрицу уравнения
beq=0;
x = linprog(f,A,b,Aeq,beq,lb,ub) %выводим необходимые нам значения
x =
0.0000
0.5000
0.5000
Задача 2:
Фирма изготавливает два вида красок для внутренних (В) и наружных (Н) работ. Для этих производств используют исходные продукты: пигмент и олифу. Расходы исходных продуктов и их максимальные суточные запасы указаны в таблице.
| Исходный продукт | Расход исходных продусков на 1 т краски | Суточный запас, т | |
| Краска Н | Краска В | ||
| Пигмент, т | |||
| Олифа, т |
Изучение рынка сбыта показало, что суточный спрос на краску для наружных (внутренних) работ никогда не превышает 2 в сутки. Цена продажи 1т краски для наружных работ составляет 3000 ден. ед., для внутренних – 2000 ден.ед. Какое количество краски каждого вида должна производить фирма, чтобы доход от реализации был максимальным?
Решение:
f(x)=3000x1+2000x2 →max (целевая функция – прибыль от продажи).
x1 – количество (т) производимой краски для наружных работ,
x2 – количество (т) производимой краски для внутренних работ.
Ограничения, накладываемые максимальными суточными запасами пигментов:
1*x1 + 2*x2 ≤ 6
2*x1 + 1*x2 ≤ 8
Так как суточный спрос на краску для внутренних работ никогда не превышает 2 в сутки, то:
x1≤ 2 И по условию 0 ≤ x1, 0 ≤ x2
Для решения данной задачи воспользуемся решателем MATLAB linprog(f,A,b), который, по умолчанию, отыскивает минимум целевой функции f, поэтому для поиска максимума функции нужно знак ее коэффициентов изменить на противоположный:
f= [-3000 -2000]; % вектор-строка коэффициентов целевой функции
A = [1 2; 2 1]; % матрица левых частей для двух неравенств
b = [6 8]; %вектор -строка правых частей неравенств
Aeq = [ ]; %вектор-строка левой части равенства
beq = [ ]; %правая часть равенства
lb = [0 0]; % вектор-строка нижних пределов
ub = [2]; %вектор-строка значений верхних пределов ограничений
x=linprog(f,A,b,Aeq,beq,lb,ub)
x =
Графическое решение задачи
Чтобы построить границы области изменения переменных, преобразуем все неравенства в равенства, пронумеруем их и выразим 𝑥2 как функцию 𝑥1
1) 1*x1 + 2*x2 = 6
x2 = 3-0.5*x1
2) 2*x1 + 1*x2 = 8
x2 = 8-2*x1
3) 𝑥1=0,
𝑥2=0.
Целевая функция при различных значениях переменных равна некоторой константе С
4) 3000*x1+2000*x2 =C,
𝑥2=C1−1.5∗𝑥1,
где обозначено С1=С/2000.
Направление максимального роста целевой функции f задает её вектор градиент. Градиент – это вектор, компоненты которого являются частными производными функции f по 𝑥1 и 𝑥2:
𝛁𝐟= 𝒈𝒓𝒂𝒅⃗(f) = 𝒊 ⃗*𝜕𝑓𝜕𝑋1+ 𝒋⃗ *𝜕𝑓𝜕𝑋2 = 𝒊⃗*3000+𝒋⃗*2000
в рассматриваемом случае компоненты градиента равны коэффициентам при 𝑥1 и 𝑥2 в целевой функции, поскольку 𝜕𝑓𝜕𝑋1= 3000 и 𝜕𝑓𝜕𝑋2 =2000.
Вектор градиента функции f направлен вдоль прямой y =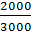 
x1 перпендикулярно линии функции (перпендикулярно прямой 3000*𝑥1+2000*𝑥2=C) и указывает направление максимального роста функции f.
Построим графики границ для области изменения переменных, вектор градиента и несколько линий целевой функции для разных значений С1.
Составим команды в кодах МАТЛАБА
x1=0:0.1:5;
x21 = 3-0.5*x1; %выражаем X2 через X1 из 1-го ограничения
x22 = 8-2*x1; %выражаем X2 через X1 из 2-го ограничения
hold on; % все остальные графики строить в тех же осях
plot(x1,x21,'b','LineWidth',2), %график первой линии ограничений
plot(x1,x22,'m','LineWidth',2),%график второй линии ограничений
plot(x1,zeros(length(x1)), 'r', 'LineWidth',2), %график нижней границы Х2 =0
%ylim([0 5]);%выделение области решений по y
%xlim([0 5]); %выделение области решений по x
plot(x1-x1+2,x1)
plot(x1,x1-x1+2)
grid minor, %мелкая сетка
fplot (@(x) 2000*x/3000, [0 2],'k','LineWidth',2.5); %построение вектора градиента целевой функции отрезком толщины 2.5 п.
gtext('gradient','Color','red','FontSize',14); %подпись вектор градиента f с выбором места вручную
axis([0,5,0,5])
%axis equal; %уравниваем масштаб по осям, чтобы градиент был зрительно перпендикулярен линии целевой функции
% % Покажем 3 линии целевой функции f по возрастанию ее значений
Val=[0.5 1 2.5]; % числовой массив констант для f
for i=1:3
C1=Val(i);
fplot(@(t) C1-1.5*t,'g'); %график линии f при разныхС
end
title('Линейное программирование. Краски'); %заголовок графика
xlabel('x1'); %подпись по оси х
ylabel('x2'), %подпись по оси y
hold off
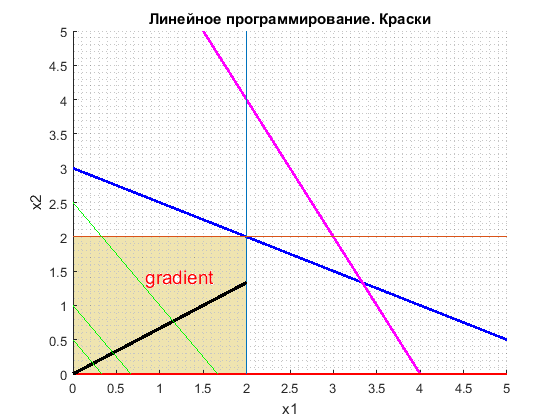
Область допустимых значений переменных 𝑥1 и 𝑥2 – это окрашенный четырехугольник. Для проверки достаточно подставить в ограничения величины переменных 𝑥1=0, 𝑥2=0 и убедиться, что они выполняются тождественно.
В направлении вектора градиента значения целевой функции возрастают f1<f2<f3, так что она достигает максимального значения на границе области в точке [2,2], которая и является решением.
Задача 3:
Кондитерская фабрика при производстве двух видов карамели – «Снежинка» и «Яблочная» - использует три вида основного сырья: сахарный песок, патоку и фруктовое пюре. Запасы сырья составляют соответственно 800 т, 600 т и 120 т. Выручка от реализации 1 т «Снежинки» составляет 108 ед.ден., а «Яблочной» - 140 ед.ден. На выпуск 1 т «Снежинки» расходуется 0.8 т сахара, 0.2 т патоки и 10 кг фруктового пюре, а на выпуск 1 т «Яблочной» - соответственно по 0.5 т, 0.4 т и 0.1 т этих видов сырья.
Необходимо найти план производства карамели, позволяющий получить наибольшую выручку.
| Сырье для изготовления карамели | Производимые виды карамели | Ограничения на расход сырья | |
| «Снежинка» | «Яблочная» | ||
| Затраты сырья на производство (1 т.) | |||
| Сахарный песок (т) | 0.8 | 0.5 | |
| Патока (т) | 0.2 | 0.4 | |
| Фруктовое пюре (т) | 0.01 | 0.1 | |
Прибыль
от продажи ( )
| 108
за 1 т
| 140
за 1 т
|
Решение:
Пусть x1 – количество карамели «Снежинка», х2 – количество карамели «Яблочная» в тоннах.
𝑓(𝑥)=108*𝑥1+140*𝑥2 - доход от реализации. Нам нужно, чтобы он был максимальным. Значит f(x) – целевая функция.
Ограничения на условия:
0.8𝑥1+0.5𝑥2≤800
0.2𝑥1+0.4𝑥2≤600
0.01𝑥1+0.1𝑥2≤120.
И по условию 𝑥1>0,𝑥2>0.
Для решения задачи воспользуемся решателем MATLAB linprog(f,A,b), который по умолчанию отыскивает минимум целевой функции f, поэтому для поиска максимума функции, нужно знак ее коэффициентов изменить на противоположный.
f=[-108 -140];
A=[0.8 0.5;0.2 0.4;0.01 0.1];
b=[800 600 120];
lb=[0 0];
ub=[];
Aeq=[];
beq=[];
x = linprog(f,A,b,Aeq,beq,lb,ub)
x =
1.0e+03 *
0.2667
1.1733
Т.е. х1 = 266.7 т, х2 = 1173 т.