| № | Способ | Рисунок | Параметры и их связи | Уравнение движения | |
| Векторный | 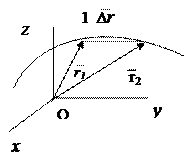
|
 - радиус-вектор - радиус-вектор

| 
| ||
| Координатный | 
|  ПЛ координаты ПЛ координаты
 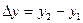



| Δ x = f 1 (t) Δ y = f 2 (t) Δ z = f 3 (t) | ||
| Естественный | 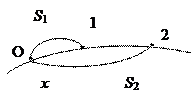
| s – КЛ координата Δ s = s 2 – s 1 | Δ s = f (t) | ||
Общий случай криволинейного движения




 |
 |
Прямая задача кинематики для поступательного и вращательного движения.
Аналогия формул
| № п/п | Величина | Линейные величины | Угловые величины | Связь скалярных линейных и угловых величин | |||
| Векторные | Скалярные | Скалярные | |||||
| Путь (изменение положения тела) | |||||||
  Перемещение по хорде
Перемещение по хорде
| Δ S = S – S 0 (м) Линейный путь по траектории | Δ φ = φ – φ 0 (pад) Угловой путь | Δ S = Δ φ . R | ||||
| Скорость (изменение положения тела за единичный промежуток времени) | |||||||
| а) | средняя за большой промежуток времени |  по хорде
по хорде
| 
| 
|  = =  . R . R
| ||
| б) | мгновенная за бесконечно малый промежуток времени | 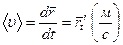
| 
| 
|  = ω . R = ω . R
| ||
| Ускорение – изменение скорости тела за единичный промежуток времени | |||||||
| а) | среднее | 
| 
| 
|  = =  . R . R
| ||
| б) | мгновенное |  внутрь кривизны
(полное)
внутрь кривизны
(полное)

| 
| 
| |||
| в) | тангенциальное (характеризует изменение υ по величине) |  Направлено
по касательной к траектории Направлено
по касательной к траектории
| ατ = ε ∙ R | ||||
Окончание таблицы
| г) | Нормальное (характеризует изменение υ по направлению) |  направлено к центру кривизны
направлено к центру кривизны
| αn = ω 2 R | ||
| д) | полное | 
| 
|
Обратная задача кинематики для поступательного и вращательного движения.
Аналогия формул
| № п/п | Поступательное движение. Линейные величины | Вращательное движение. Угловые величины | |||||
| Параметр | Формула | Вид движения | Параметр | Формула | Вид движения | Связь с дополнительными параметрами вращательного движения | |
| Линейная скорость | 
 υ 0 = υ 0 = const
υ 0 = υ 0 = const
| РУ (aτ > 0) РЗ (aτ < 0) РМ (aτ = 0) | Угловая скорость | ω = ω 0 + εt ω = ω 0 – εt ω = ω 0 = const | РУ (ε > 0) РЗ (ε < 0) РМ (ε = 0) |

| |
| Линейный путь (уравнение движения) | 


| РУ (aτ > 0) РЗ (aτ < 0) РМ (aτ = 0) | Угловой путь (уравнение движения) | 


| РУ (ε > 0) РЗ (ε < 0) РМ (ε = 0) |

|
Графики зависимости от времени для параметров
Поступательного и вращательного движения
 |
Аналогия формул динамики
Для поступательного и вращательного движения
| № п/п | Поступательное движение | Вращательное движение | |
| Мера взаимодействия | F (Н) сила | М = F · ℓ (Н · м),  момент силы
момент силы
| |
| Мера инерции | m (кг) масса | J (.) = m . r 2 (кг·м 2)
момент инерции
J (TT)0 = kф . m . R 2
обруч kф = 1
диск kф =  шар kф =
шар kф =  стержень J 0 =
стержень J 0 =  m · ℓ 2
J = J 0 + m . d 2 m · ℓ 2
J = J 0 + m . d 2
| |
| II закон Ньютона |  , , 
|  ; ; 
| |
| Количество движения |   импульс
импульс
|   момент импульса
момент импульса
| |
| Закон изменения количество движения (II закон Ньютона) | 
| 
| |
| Закон сохранения количества движения | при условии 
 = const = const  (замкнутая система)
(замкнутая система)
| при условии 
 = const = const  (замкнутая система)
(замкнутая система)
| |
| Работа постоянной силы | а)  б) А = F .∆ s .cos
б) А = F .∆ s .cos 
| А = М .∆ φ (Дж) | |
| Малый элемент работы | d A = F .d s | d A = M .d φ | |
| Работа переменной силы | А = 
| А = 
| |
| Мощность а) средняя б) мгновенная |   (Вт) (Вт)
|   (Вт) (Вт)
| |
| Энергия а) кинетическая (движения) б) потенциальная (взаимодействия) | Ек = 
| Ек = 
| |
для движения с незакреплённой осью 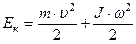
| |||
| Закон сохранения механической энергии | Е = Ек + Еn в замкнутых системах с консервативными силами |