Лабораторная работа 1
Движение заряженных частиц в континуальных электромагнитных полях.
Моделирование опыта Резерфорда
Цель работы:
– изучить движение заряженных частиц в различных электромагнитных полях.
Теоретические сведения
Моделирование движения частиц в электромагнитном поле практически ничем не отличается от моделирования движения под действием переменных сил. При движении необходимо учитывать электромагнитные силы.
Сила Кулона. Между любыми двумя электрическими точечными зарядами действуют силы, прямо пропорциональные произведению зарядов и обратно пропорциональные квадрату расстояния между ними (рис. 1)
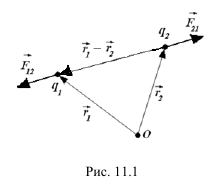Рис.1.
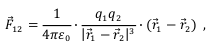|  где F12 – сила Кулона, действующая на точку с зарядом q1, со стороны другой материальной точки, обладающей зарядом q2, r1 и r2 – соответственно радиус-вектора первой и второй точек. Коэффициент ε0 называется диэлектрической постоянной и численно равен: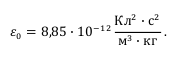 
|
Сила, действующая на заряженную частицу в электрическом поле:
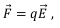
где q - заряд рассматриваемой частицы, E – вектор напряженности электрического поля.
Сила Лоренца:
где V - скорость рассматриваемой частицы, В − вектор индукции магнитного поля.
Основы программирования в пакете MATLAB.
Компьютерная программа с пакетами расширения, входящими в систему MATLAB, позволяет эффективно использовать её возможности в самых новейших областях науки и техники, таких как средства анализа и обработки сигналов и изображений, идентификация объектов и систем управления, нейронные сети и т.д. По своей структуре MATLAB напоминает наиболее популярный для обучения в средней в школе язык программирования Pascal, но в нем содержатся встроенные пакеты математических программ, которые позволяют получить желаемый результат достаточно быстро. Кроме того, MATLAB имеет возможность диалога с другими программами (MS Word, MS Exel, Maple и др).
|
|
При открытии пакета возникает несколько окон (рис. 1.1), среди которых основным является Command Window (окно команд). Работать в окне команд удобно при небольших расчетах, при компьютерном моделировании необходимо завести файл. Для это нужно щелкнуть File (файл) → New (новый) → M-File (М-файл). Откроется окно Untitled (безымянный) (рис. 1.2), в котором можно писать программу.
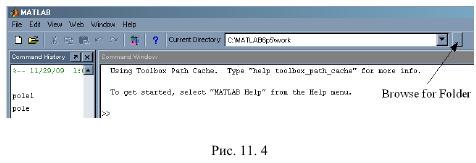
Рис.1.1.
После сохранения М-файла нужно проследить, чтобы Current Directory (директория) была настроена на нужную папку. Сменить папку можно через раскрывающейся список или с помощью кнопки Browse for Folder (рис. 1.1).
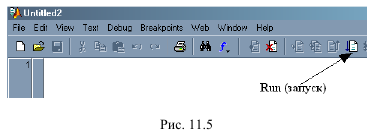
Рис.1.2.
Писать программу можно обычными средствами MS Word, запускается при нажатии на кнопку Run (рис. 1.2). Сообщения об ошибках выдаются после запуска программы в командном окне. При написании программы в пакете MATLAB нужно учитывать следующие особенности:
- знаком присваивания является символ «= »:
- каждая строка заканчивается символом «; », если его нет, программа не прекращает работу, но вычисленные в этой строке выражения выдаются на экран в командном окне;
- запись комментариев осуществляется после символа «% »;
-проекции векторов, как и элементы одномерного массива, записываются в строку в квадратных скобках через пробел;
- ссылка на элемент массива осуществляется через его индекс, который записывается в круглых скобках.
MATLAB выполняет масштабирование самостоятельно таким образом, чтобы график занял всю область построения. В случае необходимости другого масштабирования (например, для сравнения графиков) можно воспользоваться опцией axis([xmin xmax ymin ymax zmin zmax]), которая пишется в М-файле после фразы о построении графика «plot(…)». Величины, стоящие в скобках − пределы изменения соответствующих координат. Для построения графиков в одних координатных осях пользуются опцией hold on, которую можно написать, например, в окне команд.
|
|
Задание. Построить траектории движения заряженных частиц, влетающих в стационарное магнитное поле под разными углами α (α1 =0°; α2 =30°; α3 =60°; α4 =90°). Сделать вывод о зависимости формы траектории частицы от угла α. Модуль вектора магнитной индукции B, заряд q, массу m и начальную скорость V0 частицы взять из таблицы:
alfa=0; pi/6; pi/3; pi/2;
q=2;
B= [3 0 0];
m=1; r= [0 0 0];
v= [1*cos(alfa) 1*sin(alfa) 0];
X= [];
Y= [];
Z= [];
T=10;
dt=0.001;
for t=0:dt:T;
X=[X r(1)];
Y=[Y r(2)];
Z=[Z r(3)];
F=q* cross (v,B);
a=F/m;
v=v+a*dt;
r=r+v*dt;
end;
plot3(X,Y,Z)
grid
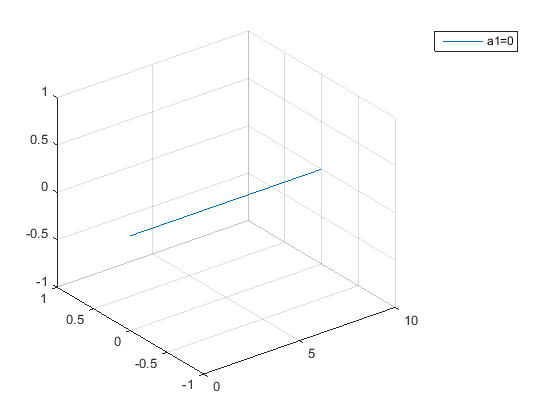
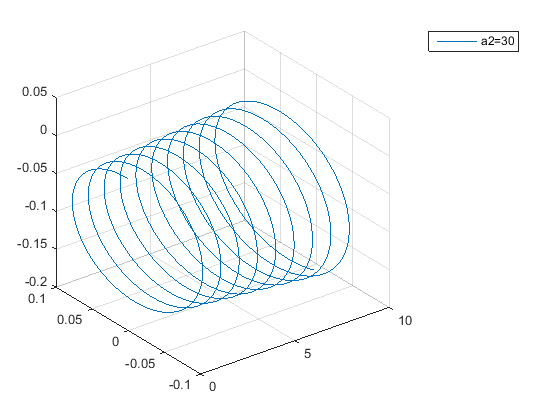
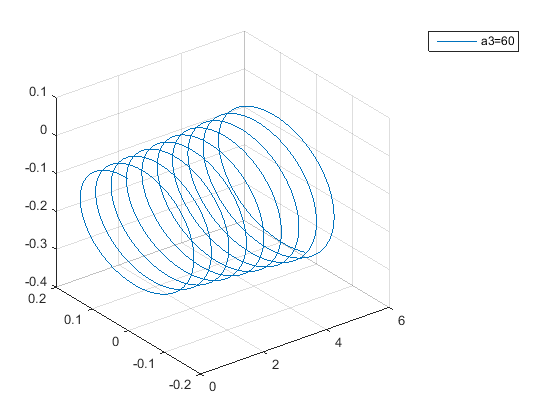
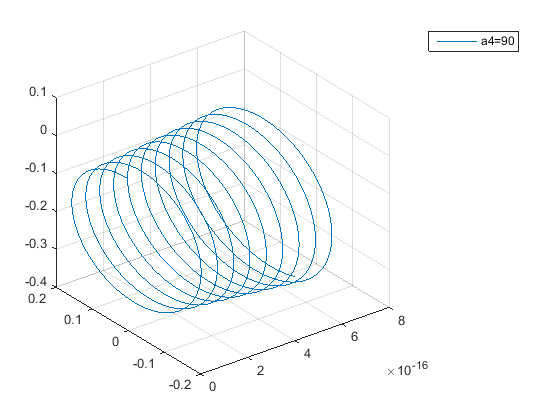
Вывод:
Были построены траектории движения заряженных частиц, влетающих в магнитное поле под разными углами α (α1 =0°; α2 =30°; α3 =60°; α4 =90°).
В результате:
α1 =0° траектория принимает вид прямой;
α2 =30° график принимает вид спирали;
α3 =60° увеличение частоты вращения частицы;
α4 =90° небольшое увеличение радиуса спирали относительно предыдущих значений.