Содержание:
Стр.
1. Цепи с сосредоточенными и цепи с распределёнными параметрами.. 2
2. Двухпроводная линия и её эквивалентная схема................... 3
3. Телеграфные уравнения...................................... 4
4. Решение телеграфных уравнений для линии без потерь............ 6
5. Вторичные параметры линии без потерь......................... 8
5.1. Волновое сопротивление................................ 8
5.2. Входное сопротивление.................................. 8
5.3. Коэффициент отражения................................ 9
5.4. Волновое число и фазовая скорость....................... 9
6. Режимы работы линии без потерь............................. 10
6.1. Режим бегущих волн.................................. 10
6.2. Режим стоячих волн................................... 12
6.3. Режим смешанных волн................................ 14
7. Коэффициент стоячей волны................................. 14
КОНТРОЛЬНЫЕ ВОПРОСЫИ ЗАДАНИЯ......................... 16
ДОПОЛНТЕЛЬНОЕ ЗАДИНИЕ.................................. 17
ЛИТЕРАТУРА................................................. 17
1. Цепи с сосредоточенными
и цепи с распределёнными параметрами
Процесс в цепи называется квазистационарным, если он протекает настолько медленно, что в любой момент времени мгновенное значение тока можно считать одинаковым в разных сечениях любого данного участка цепи. В противном случае процесс в цепи будет волновым.
Пусть τ – характерное время изменения какого-либо параметра процесса, например, время роста или спада напряжения или тока в данном сечении провода, l – характерная длина цепи, υ – скорость распространения процесса по цепи (обычно υ= с =3·108 м/с). Тогда условием квазистационарности процесса в данной цепи будет:
l ≪ с τ. (1)
Для синусоидальных процессов в качестве характерного времени изменения тока или напряжения можно взять четверть периода (τ= Т /4), и в этом случае условие (1) принимает вид:
l ≪ 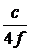 , (2)
, (2)
где f =1/ Т – частота синусоидального процесса. Символ «≪» обычно означает «меньше, по крайней мере, на порядок, т.е. в 10 раз».
Для участков или полных цепей, удовлетворяющих условию квазистационарности (1) или (2), можно применять уравнения Ома и Кирхгофа.
Если элементы R, L и C некоторой цепи можно считать локализованными (сосредоточенными) на малых участках, соединённых сколь угодно длинными идеальными проводниками, то говорят, что это цепь с сосредоточенными параметрами. При этом предполагается, что выполнено условие квазистационарности. Так например, для процессов с частотами f ~100 МГц условие (2) справедливо лишь для цепей длиной l ≪1 м (т.е. при l ≤10 см). Следовательно, в цепях настольных размеров (l ~1 м) условие (2) выполнено уже не будет. В них уже нельзя пользоваться уравнениями Ома и Кирхгофа, ток в разных сечениях данного участка цепи будет разным, а напряжение между узлами неопределённо, поскольку теперь оно будет зависеть от конфигурации проводов измерительной цепи (работа поля Е будет зависеть от формы пути). При этом каждому малому участку обыкновенного соединительного провода уже необходимо приписывать некоторое сопротивление, ёмкость и индуктивность. В этом случае говорят, что цепь обладает распределёнными параметрами R, L и C.
Цепь с распределёнными параметрами может содержать и обычные сосредоточенные элементы – резисторы, катушки и конденсаторы, только их размеры должны заведомо удовлетворять условию (2). Кроме того, следует иметь в виду, что на высоких частотах каждый из этих элементов уже не проявляет себя в своём чистом виде, а приобретает свойства других, т.е., например, резистор приобретает емкостные и индуктивные свойства.
1.2. Двухпроводная линия и её эквивалентная схема
Двухпроводная линия (далее просто – линия) – это два длинных параллельных провода, в которых генератором могут возбуждаться токи высокой частоты. Линия называется длинной, если выполнены условия:
l ≥λ=υ/ f, d ≪λ/4, (3)
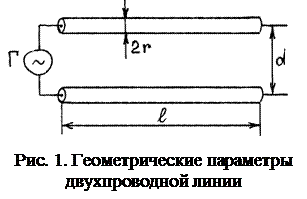 где f – частота генератора, λ – длина волны в линии, υ – скорость распространения возмущения вдоль линии (как будет показано далее, для линии в воздухе или в вакууме υ= с =3·108 м/с), l – длина линии, d – расстояние между проводами (рис. 1). Кроме того, для простоты дальнейших рассуждений и формул будем считать провода линии тонкими, т.е. полагать, что их радиусы r ≪ d.
где f – частота генератора, λ – длина волны в линии, υ – скорость распространения возмущения вдоль линии (как будет показано далее, для линии в воздухе или в вакууме υ= с =3·108 м/с), l – длина линии, d – расстояние между проводами (рис. 1). Кроме того, для простоты дальнейших рассуждений и формул будем считать провода линии тонкими, т.е. полагать, что их радиусы r ≪ d.
 Так как для длинной линии не выполнено условие (2), то она является типичной цепью с распределёнными параметрами и процессы в ней будут не квазистационарными, а волновыми. Для их анализа представим линию состоящей из множества малых участков длиной dx. Каждый такой участок обладает некоторыми активным сопротивлением dR, индуктивностью dL, ёмкостью dC, а также проводимостью утечки dG. Тогда эквивалентную схему линии можно изобразить в виде, показанном на рис. 2.
Так как для длинной линии не выполнено условие (2), то она является типичной цепью с распределёнными параметрами и процессы в ней будут не квазистационарными, а волновыми. Для их анализа представим линию состоящей из множества малых участков длиной dx. Каждый такой участок обладает некоторыми активным сопротивлением dR, индуктивностью dL, ёмкостью dC, а также проводимостью утечки dG. Тогда эквивалентную схему линии можно изобразить в виде, показанном на рис. 2.
Однако практически вместо величин dR, dL, dC и dG удобно ввести так называемые погонные параметры линии, т.е. параметры, относящиеся к единице её длины:
R 0=  − погонное активное сопротивление линии,
− погонное активное сопротивление линии,
L 0= 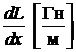 − погонная индуктивность линии,
− погонная индуктивность линии,
С 0= 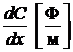 − погонная ёмкость линии,
− погонная ёмкость линии,
G 0=  − погонная проводимость утечки в линии.
− погонная проводимость утечки в линии.
Если величины R 0, L 0, C 0 и G 0 одинаковы во всех сечениях линии, то линия называется однородной.
1.3. Телеграфные уравнения
Для длинной линии в целом пользоваться уравнениями Ома и Кирхгофа нельзя, поскольку для неё не выполнено условие (2). Однако их можно применить для любого малого её участка, так как по отношению к поперечному размеру линии это условие выполнено.
Пусть в однородной длинной линии возбуждаются электрические колебания. Поскольку условие квазистационарности для неё не выполнено, то напряжение между проводами и ток в них будут являться непрерывными функциями времени t и координаты х вдоль линии: и = и (x, t), i = i (x, t); причём ток, текущий по одному из проводов, равен и противоположно направлен току, текущему напротив него вдоль другого провода.
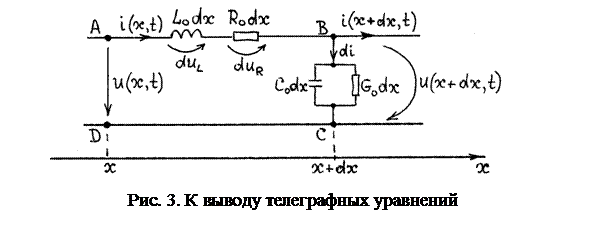 Разобъём линию на малые участки длиной dx. На каждом таком участке активное сопротивление равно R 0 dx, индуктивность – L 0 dx, ёмкость – C 0 dx, проводимость утечки – G 0 dx (рис. 3). Пусть i (x, t) и и (x,t) – ток в проводах и напряжение между ними в начале участка dx, а i (x + dx, t) и и (x + dx,t) – в конце. Запишем второе уравнение Кирхгофа для контура ABCD, обходя его по часовой стрелке:
Разобъём линию на малые участки длиной dx. На каждом таком участке активное сопротивление равно R 0 dx, индуктивность – L 0 dx, ёмкость – C 0 dx, проводимость утечки – G 0 dx (рис. 3). Пусть i (x, t) и и (x,t) – ток в проводах и напряжение между ними в начале участка dx, а i (x + dx, t) и и (x + dx,t) – в конце. Запишем второе уравнение Кирхгофа для контура ABCD, обходя его по часовой стрелке:
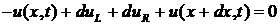 ,
,
или
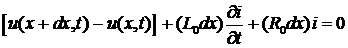 .
.
Деля это уравнение на dx и учитывая, что
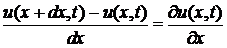 ,
,
получаем
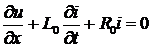 . (4а)
. (4а)
Запишем теперь первое уравнение Кирхгофа для узла В:
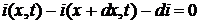 ,
,
где
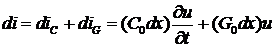 .
.
Таким образом,
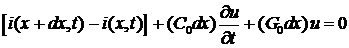 .
.
Точно так же, деля это уравнение на dx, получаем
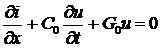 . (4б)
. (4б)
Уравнения (4а) и (4б) являются основными для линии с распределёнными параметрами и называются телеграфными уравнениями.
Далее везде будем предполагать, что линия является однородной и потери в ней отсутствуют, т.е. R 0=0, G 0=0, а L 0 и С 0 – постоянны. Тогда телеграфные уравнения (4а) и (4б) примут вид:
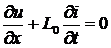 , (5а)
, (5а)
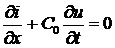 . (5б)
. (5б)
Покажем, что уравнения (5а) и (5б) описывают волновой процесс в линии. Для этого продифференцируем (5а) по х, а (5б) по t и, подставив затем 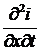 из второго уравнения в первое, получим
из второго уравнения в первое, получим
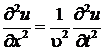 , (6)
, (6)
где
υ= 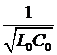 . (7)
. (7)
Уравнение (6) называется волновым. Его общее решение имеет вид
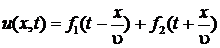 , (8)
, (8)
где f 1 и f 2 – произвольные дважды дифференцируемые функции, первая из которых описывает процесс распространения волн напряжения вправо (по оси х) со скоростью υ и называется прямой (падающей) волной а вторая – влево (против оси х) и называется обратной (отражённой) волной. Конкретный вид функций f 1 и f 2 определяется формой возбуждающего сигнала.
Из (5а) и (5б) аналогично легко получить такое же волновое уравнение для тока:
 ,
,
общим решением которого также является функция вида
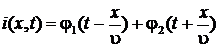 ,
,
описывающая волны тока вправо и влево по линии со скоростью υ.
4. Решение телеграфных уравнений для линии без потерь
при установившемся синусоидальном процессе
Пусть выходное напряжение генератора является синусоидальным с частотой ω. При подключении к нему линии в ней начнётся переходный процесс, длительность которого зависит от длины линии и потерь в ней. Реально он заканчивается за время порядка 10−6 с, и в линии устанавливается стационарный волновой режим, который и будем рассматривать в дальнейшем. При этом режиме напряжение и ток в каждом сечении линии будут меняться по синусоидальному закону с частотой генератора ω, а их амплитуды и фазы зависеть от координаты х. В связи с этим, решение телеграфных уравнений (5а) и (5б) удобно искать в комплексном виде:
u (x,t)→ 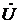 (х)
(х) 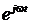 , i (x,t)→
, i (x,t)→ 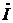 (х)
(х) 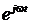 , (9)
, (9)
где 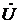 (х)=
(х)=  − комплексная амплитуда (комплекс) напряжения,
− комплексная амплитуда (комплекс) напряжения,
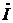 (х)=
(х)= 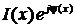 − комплексная амплитуда (комплекс) тока,
− комплексная амплитуда (комплекс) тока,
U (x) и I (x) – действительные амплитуды напряжения и тока,
φ(х) и ψ(х) – начальные фазы напряжения и тока.
Комплексная запись решения (9) используется для удобства вычислений. Она даёт возможность перейти от уравнений в частных производных (5а) и (5б) к обыкновенным дифференциальным уравнениям относительно комплексов 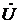 и
и 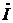 . А чтобы вернуться к обычной (временнóй) форме записи мгновенных значений, надо после определения неизвестных величин
. А чтобы вернуться к обычной (временнóй) форме записи мгновенных значений, надо после определения неизвестных величин 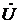 (х) и
(х) и 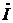 (х) взять их реальные или мнимые части, например,
(х) взять их реальные или мнимые части, например,
и (x, t)=Im 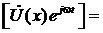 Im
Im 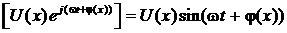 .
.
Итак, подставим искомые функции вида (9) в уравнения (5а) и (5б). Получим систему обыкновенных дифференциальных уравнений для комплексов 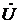 (х) и
(х) и 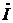 (х):
(х):

Подставляя теперь 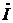 из (10а) в (10б), получим одно уравнение второго порядка для комплекса
из (10а) в (10б), получим одно уравнение второго порядка для комплекса 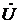 :
:
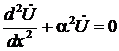 , (11)
, (11)
где
 . (12)
. (12)
Общее решение уравнения (11) имеет вид
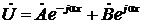 , (13а)
, (13а)
где 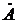 и
и 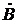 − неопределённые пока комплексные коэффициенты.
− неопределённые пока комплексные коэффициенты.
Чтобы найти 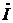 , теперь достаточно подставить выражение
, теперь достаточно подставить выражение 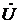 из (13а) в (10а); с учётом (12) это даёт:
из (13а) в (10а); с учётом (12) это даёт:
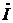 =
= 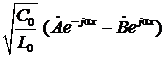 . (13б)
. (13б)
Первые слагаемые в (13а) и (13б) – это комплексные амплитуды напряжения и тока прямой волны, а вторые – обратной. Действительно, например, первое слагаемое (13а) соответствует волне
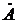
 , (14)
, (14)
где U пр – амплитуда прямой волны. Здесь U пр 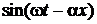 и есть тот конкретный вид функции
и есть тот конкретный вид функции 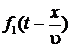 из (8), представляющей прямую волну общего вида.
из (8), представляющей прямую волну общего вида.
Важнейшим параметром линии является её волновое сопротивление.
Определение. Отношение комплексных амплитуд напряжения и тока в прямой (или в обратной) волне называется волновым сопротивлением линии (ρ). Таким образом, из (13а) и (13б), по определению, имеем:
ρ= 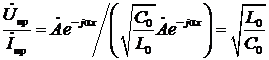 [Ом]. (15)
[Ом]. (15)
Коэффициенты 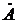 и
и 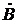 в (13а) и (13б) определяются из граничных условий, а именно – по измеряемым току и напряжению на нагрузке в конце линии. Пусть в конце линии, в сечении х = l установлена нагрузка, имеющая комплексное сопротивление Z н, а напряжение и ток на ней равны
в (13а) и (13б) определяются из граничных условий, а именно – по измеряемым току и напряжению на нагрузке в конце линии. Пусть в конце линии, в сечении х = l установлена нагрузка, имеющая комплексное сопротивление Z н, а напряжение и ток на ней равны
 и
и 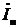 (рис. 4). Тогда для х = l уравнения (13а) и (13б) примут вид:
(рис. 4). Тогда для х = l уравнения (13а) и (13б) примут вид:

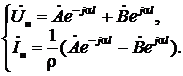
Складывая и вычитая эти уравнения, получаем:
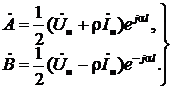 (16)
(16)
Теперь (13а) и (13б) с подстановкой в них (16) принимают вид:

Из этих уравнений видно, что координату удобнее отсчитывать от нагрузки влево, т.е. положить у = l − х, как показано на рис. 4. И тогда, учитывая, что
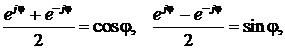
окончательно получаем для комплексных амплитуд напряжения и тока в линии:
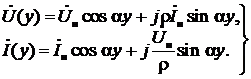 (17)
(17)
Комплексные амплитуды  и
и 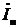 определяются мощностью генератора. Кроме того, они связаны законом Ома:
определяются мощностью генератора. Кроме того, они связаны законом Ома:  = Z н
= Z н 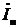 .
.
5. Вторичные параметры линии без потерь
Вторичными называются параметры, выражаемые через первичные – погонные величины R 0, L 0, C 0 и G 0 и импеданс нагрузки Z н. Для линии без потерь R 0=0 и G 0=0. Ко вторичным параметрам относятся: волновое сопротивление, входное сопротивление, коэффициент отражения, волновое число и фазовая скорость.
5.1. Волновое сопротивление
Определение волнового сопротивления было дано в разделе 1.4, а его выражение через первичные параметры – формулой (15):
ρ= 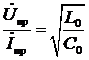 .
.
Видно, что волновое сопротивление линии без потерь является действительным числом и не зависит от частоты.
Известно, что погонные индуктивность и ёмкость двухпроводной линии, показанной на рис. 1, в приближении r ≪ d следующие:
L 0= 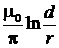 , С 0=
, С 0= 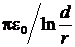 , (18)
, (18)
где ε0 и μ0 – электрическая и магнитная постоянные. Следовательно, волновое сопротивление двухпроводной линии
ρ= 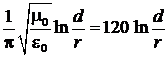 [Ом]. (19)
[Ом]. (19)
Так как обычно отношение d/r ~10…100, то волновое сопротивление такой линии имеет порядок нескольких сотен ом.
5.2. Входное сопротивление
Определение. Отношение комплексных амплитуд напряжения и тока в данном сечении линии называется входным сопротивлением линии в этом сечении:
Z вх= 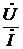 .
.
Подставляя сюда 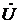 и
и 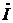 из (17), получаем для входного сопротивления линии в данном сечении у:
из (17), получаем для входного сопротивления линии в данном сечении у:
Z вх=  , (20)
, (20)
где
Z н= 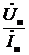
− импеданс нагрузки. Таким образом, входное сопротивление является, вообще говоря, числом комплексным, причём Z вх= Z вх(ρ, Z н, ω, у), а на конце линии (при у =0) Zвх= Z н.
5.3. Коэффициент отражения
Волны токов и напряжений, возбуждаемые в линии генератором, доходят до нагрузки Z н и, вообще говоря, частично или полностью отражаются от неё обратно в линию, так что коэффициент 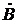 в (13а) и (13б), соответствующий комплексной амплитуде отражённых волн, в общем случае не равен нулю.
в (13а) и (13б), соответствующий комплексной амплитуде отражённых волн, в общем случае не равен нулю.
Определение. Отношение комплексных амплитуд напряжений (или токов) отражённой и падающей волн в некотором сечении линии называется коэффициентом отражения  в этом сечении:
в этом сечении:
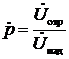 . (21)
. (21)
Из (13а) и (16) имеем:
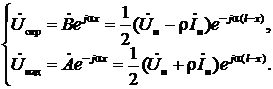
Тогда
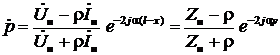 .
.
Обычно представляет интерес не сам коэффициент отражения, а его модуль, поэтому далее везде под коэффициентом отражения будем понимать величину
 . (22)
. (22)
Видно, что всегда 0≤ р ≤1. Действительно, пусть Z н= R н+ jX н, тогда
 ≤1. (23)
≤1. (23)
5.4. Волновое число и фазовая скорость
Рассмотрим аргумент синуса (ω t −α х) в формуле (14), который называется фазой волны. Если число ω характеризует скорость изменения фазы в данном сечении линии х, то число α − «скорость» изменения фазы вдоль линии в данный момент t. Это число α называется волновым числом. Оно «произошло» из уравнения (11) и выражается через погонные параметры линии и частоту ω формулой (12)
 .
.
Определение. Фазовой скоростью υ волны называется скорость перемещения вдоль линии неизменного фазового состояния, т.е. какой-либо фиксированной фазы напряжения или тока.
Выразим фазовую скорость через другие параметры линии. Для этого запишем условие постоянства фазы: (ω t −α х)=const. Дифференцируя это по времени и учитывая (12), получаем:
υ= 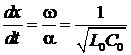 ,
,
что совпадает с (7). Подстановка сюда выражений (18) даёт численное значение фазовой скорости волн в двухпроводной линии:
υ= 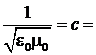 3·108 м/с.
3·108 м/с.
Таким образом, вóлны токов и напряжений бегут по линии без потерь со скоростью света в вакууме.
Определение. Расстояние λ, которое волна пробегает за период Т, называется длиной волны:
λ=υ T = 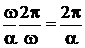 . (24)
. (24)
Полагая υ= с, Т =1/ f, получаем: λ= с/f, где f – частота генератора.
6. Режимы работы линии без потерь
6.1. Режим бегущих волн
Если линия нагружена на активное сопротивление, равное волновому, т.е. Z н=ρ, то, как следует из (22), коэффициент отражения р =0, а из определения (21) получаем, что 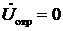 (и
(и 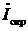 =0), а, следовательно, и
=0), а, следовательно, и 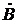 =0. Таким образом, при Z н=ρ в линии существуют только падающие волны и она становится эквивалентной полубесконечной линии без потерь. Поэтому нагрузка Z н=ρ называется согласованной, а соответствующий режим в линии – режимом бегущих волн. В этом режиме в линии происходит идеальная канализация высокочастотной энергии, которая полностью поглощается нагрузкой. Для режима бегущих волн (
=0. Таким образом, при Z н=ρ в линии существуют только падающие волны и она становится эквивалентной полубесконечной линии без потерь. Поэтому нагрузка Z н=ρ называется согласованной, а соответствующий режим в линии – режимом бегущих волн. В этом режиме в линии происходит идеальная канализация высокочастотной энергии, которая полностью поглощается нагрузкой. Для режима бегущих волн (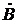 =0) уравнения (13а) и (13б) принимают вид:
=0) уравнения (13а) и (13б) принимают вид:
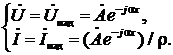
Но учитывая, что 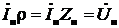 , из первого уравнения (16) получаем:
, из первого уравнения (16) получаем:
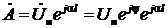 ,
,
где U н – действительная амплитуда напряжения на нагрузке, ψ – некоторая его начальная фаза. Для простоты, не искажающей существа процесса, можно положить ψ=−α l, так что 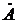 = U н, и тогда
= U н, и тогда

Следовательно, для мгновенных значений напряжения и тока в линии получаем:

Эти функции и представляют бегущие синусоидальные волны напряжений и токов в линии. Из них видно, что в режиме бегущих волн:
● амплитуды напряжения и тока постоянны на всей линии:
U =const= U н, I =const= I н;
● напряжение и ток в каждом сечении линии изменяются синфазно, т.е. сдвиг фаз между ними φ=0; а это означает, что вдоль линии от генератора к нагрузке переносится активная мощность
P = 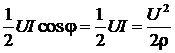 ,
,
которая вся и поглощается нагрузкой.
 Но высокочастотные напряжения и токи создают вокруг проводов переменные электрическое и магнитное поля, ориентированные в плоскости поперечного сечения линии, как показано на рис. 5. Следовательно, вдоль линии бегут волны электрического и магнитного полей − электромагнитные волн ы. Можно показать. что энергия от генератора к нагрузке переносится именно этими волнами, а провода линии лишь задают направление переноса. Плотность потока электромагнитной энергии характеризуется вектором Пойнтинга
Но высокочастотные напряжения и токи создают вокруг проводов переменные электрическое и магнитное поля, ориентированные в плоскости поперечного сечения линии, как показано на рис. 5. Следовательно, вдоль линии бегут волны электрического и магнитного полей − электромагнитные волн ы. Можно показать. что энергия от генератора к нагрузке переносится именно этими волнами, а провода линии лишь задают направление переноса. Плотность потока электромагнитной энергии характеризуется вектором Пойнтинга
П = Е × Н= 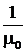 (Е × В),
(Е × В),
который в данном случае постоянен по величине и направлен вдоль линии от генератора к нагрузке.
Так как поля Е и В в двухпроводной линии имеют только поперечные компоненты, а фронт электромагнитной волны (т.е. поверхность постоянной фазы волны) является плоским, то такие волны называются плоскими поперечными волнами типа ТЕМ (Transverse Electric-Magnetic).
Как следует из (20), в режиме бегущих волн (т.е. при Z н=ρ) входное сопротивление в любом сечении линии Z вх=ρ, т.е. постоянно и чисто активно.
6.2. Режим стоячих волн
Если амплитуды падающих и отражённых волн равны, то говорят, что линия работает в режиме стоячих волн. В этом режиме, как следует из (21), р =1.
Из формул (22) и (23) видно, что режим стоячих волн в линии реализуется в следующих трёх случаях:
● Z н=∞ (линия на конце разомкнута);
● Z н=0 (короткозамкнутая линия);
● Z н= jX н (линия, нагруженная на реактивное сопротивление).
Ограничимся анализом процессов в линии в первых двух вариантах.
6.2.1. Разомкнутая линия (Z н=∞)
При Z н=∞ ток 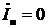 , следовательно, уравнения (17) примут вид:
, следовательно, уравнения (17) примут вид:
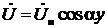 ,
,  ;
;
и для мгновенных значений напряжения и тока в линии получаем:
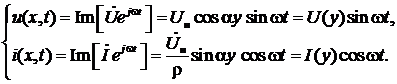
Эти соотношения описывают стоячие волны в линии, которые характеризуются следующими свойствами:
1. Амплитуды напряжения и тока в линии зависят от координаты у:
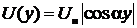 ,
, 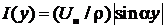 . (25)
. (25)
Максимальные значения амплитуды напряжения (U max= U н) называются пучностями напряжения, а минимальные (U min=0) – узлами напряжения. Видно, что координаты пучностей напряжения определяются из условия
cosα y =±1, т.е. α у =π k (k =0, 1, 2, …),
а координаты узлов напряжения – из условия
cosα y =0, т.е. α у =π(k +1/2) (k =0, 1, 2, …).
Тогда, учитывая. что α=2π/λ (соотношение (24)), получаем для координат пучностей и узлов напряжения:
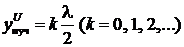 ,
, 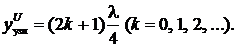
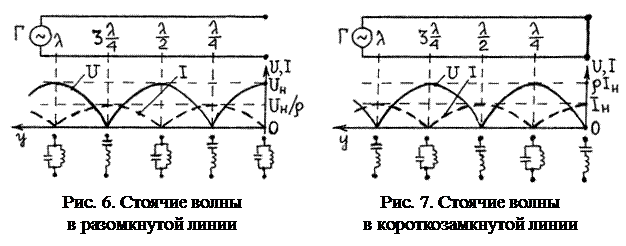 Аналогично определяются положения пучностей и узлов тока; при этом получается, что узлы тока совпадают с пучностями напряжения и наоборот (рис.6).
Аналогично определяются положения пучностей и узлов тока; при этом получается, что узлы тока совпадают с пучностями напряжения и наоборот (рис.6).
2. Фаза колебаний напряжения между узлами не зависит от у, а при переходе через узел скачком меняется на π. Аналогично для фазы тока.
3. В каждом сечении линии разность фаз между мгновенными значениями тока и напряжения φ=π/2, следовательно, активная мощность по линии не переносится (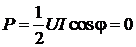 ); энергия лишь на локальных участках превращается из электрической в магнитную и наоборот.
); энергия лишь на локальных участках превращается из электрической в магнитную и наоборот.
Как видно из (20), входное сопротивление разомкнутой линии
Z вх= 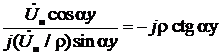 .
.
При α у =π k, т.е. при у = k 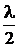 (k =0, 1, 2, …), т.е. в узлах тока, Z вх=∞, как у параллельного контура; а при у =
(k =0, 1, 2, …), т.е. в узлах тока, Z вх=∞, как у параллельного контура; а при у = 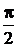 +π k =(2 k +1)
+π k =(2 k +1) 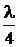 (k =0, 1, 2, …), т.е. в узлах напряжения, Z вх=0, как у последовательного колебательного контура.
(k =0, 1, 2, …), т.е. в узлах напряжения, Z вх=0, как у последовательного колебательного контура.
Определение. Отрезки линии у = k 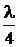 (k =1, 2, …), ведущие себя как параллельный или последовательный контуры, называются резонансными.
(k =1, 2, …), ведущие себя как параллельный или последовательный контуры, называются резонансными.
Резонансные отрезки имеют одно важное свойство: из формулы (20) следует, что при любой нагрузке Z н входное сопротивление четвертьволновых отрезков (k =1, 3, 5, …)
Z вх 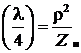 , (26а)
, (26а)
а входное сопротивление полуволновых отрезков (k =2, 4, 6, …)
Z вх 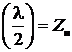 . (26б)
. (26б)
Последнее означает, что полуволновый отрезок линии с нагрузкой Z н эквивалентен самой нагрузке Z н.
6.2.2. Короткозамкнутая линия (Z н=0)
При Z н=0 напряжение на конце линии 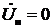 , следовательно, уравнения (17) принимают вид:
, следовательно, уравнения (17) принимают вид:
 ,
, 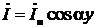 ;
;
и для мгновенных значений напряжения и тока получаем:
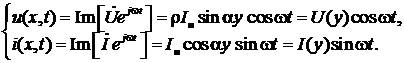
Эти соотношения, как и в предыдущем случае Z н=∞, описывают стоячие волны, только здесь координаты пучностей и узлов напряжения будут:
 ,
, 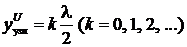 ,
,
т.е. взаимно меняются по сравнению с вариантом Z н=∞. То же самое для пуч  ностей и узлов тока (рис. 7).
ностей и узлов тока (рис. 7).
Замечание. Из формулы (26а) следует, что входное сопротивление четвертьволнового короткозамкнутого отрезка  ∞. Это свойство позволяет применять такие отрезки в качестве изолирующих креплений линии (рис. 8), так как они не шунтируют линию ни в каком месте и не нарушают режим её работы.
∞. Это свойство позволяет применять такие отрезки в качестве изолирующих креплений линии (рис. 8), так как они не шунтируют линию ни в каком месте и не нарушают режим её работы.
6.3. Режим смешанных волн
Если линия нагружена на сопротивление Z н, не равное 0, ∞, jX н или ρ, то в ней устанавливается режим смешанных волн, когда в линии существуют отражённые волны, но меньшей амплитуды, чем падающие, поскольку часть энергии поглощается активной компонентой нагрузки. Ограничимся рассмотрением варианта чисто активной нагрузки, когда Z н= R н≠ρ.
Как видно из (22), при Z н= R н коэффициент отражения
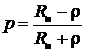 . (27)
. (27)
Уравнения (17) принимают вид:
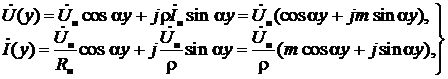
где m= ρ/ R н. Отсюда для действительных амплитуд получаем:
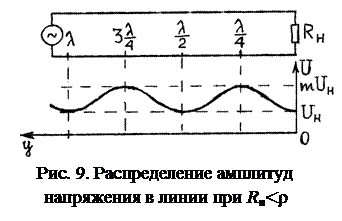
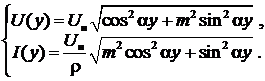
На рис. 9 в качестве примера показан график U (y) при m >1, т.е. при R н<ρ.
Смешанную волну можно представить в виде суперпозиции бегущей и стоячей волн.
7. Коэффициент стоячей волны
Режим работы линии можно характеризовать коэффициентом отражения  , определяемым формулой (21). Однако разделить падающие и отражённые волны для измерения их амплитуд практически трудно, поэтому для количественной оценки режима работы линии вводится другая величина, связанная с коэффициентом отражения, но легко измеряемая. Эта величина называется коэффициентом стоячей волны (КСВ) и определяется как отношение максимальной и минимальной амплитуд напряжения (или тока) в линии*):
, определяемым формулой (21). Однако разделить падающие и отражённые волны для измерения их амплитуд практически трудно, поэтому для количественной оценки режима работы линии вводится другая величина, связанная с коэффициентом отражения, но легко измеряемая. Эта величина называется коэффициентом стоячей волны (КСВ) и определяется как отношение максимальной и минимальной амплитуд напряжения (или тока) в линии*):
КСВ= 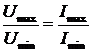 . (28)
. (28)
Из этого определения следует, что
● в режиме бегущих волн, т.е. при Z н=ρ: КСВ=1;
● в режиме стоячих волн, т.е. при Z н=0, ∞ или jХ н: КСВ=∞;
● в режиме смешанных волн, т.е. при Z н= R н+ jХ н: 1<КСВ<∞.
Из определения (28) легко установить связь КСВ и коэффициента отражения. В сечении линии. где U = U max, падающая и отражённая волны складываются в фазе, а где U = U min – в противофазе, поэтому можно записать:
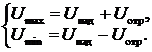
Отсюда
КСВ= 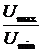 =
= 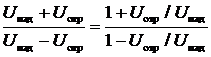 ,
,
или, с учётом (21),
КСВ= 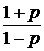 , (29)
, (29)
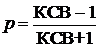 . (30)
. (30)
Чем ближе КСВ к единице, тем лучше согласование нагрузки с линией. Согласование считается
● хорошим, если КСВ≤1,5 (при этом р ≤0,2),
● удовлетворительным, если 1,5<КСВ≤3 (0,2< р ≤0,5),
● плохим, если КСВ>3 (р >0,5).
Из (27) и (29) следует. что при чисто активной нагрузке Z н= R н
КСВ=  (31)
(31)
Поскольку основным назначением передающей линии является передача максимальной мощности от генератора к потребителю (к нагрузке), то важно уметь выражать КСВ через падающую и отражённую от нагрузки мощности. Так как мощность Р~U 2, то из (21) и (30) получаем долю отражённой мощности:
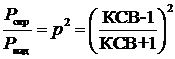 .
.
Таким образом, при хорошем согласовании, когда КСВ≤1,5, отношение 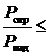 4%, а при удовлетворительном –
4%, а при удовлетворительном – 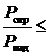 25%.
25%.
КОНТРОЛЬНЫЕ ВОПРОСЫИ ЗАДАНИЯ
1. Что такое квазистационарные процессы? Волновые процессы?
2. Что такое длинная однородная линия?
3. Изобразить эквивалентную схему длинной линии.
4. Записать волновое уравнение и общий вид его решения.
5. Установить, удовлетворяет ли волновому уравнению (6) функция 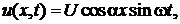 не имеющая вида (8).
не имеющая вида (8).
6. Что такое волновое сопротивление линии? Зависит ли оно от координаты сечения линии? От её геометрии? От нагрузки?
7. Вывести формулы для погонных ёмкости и индуктивности:
а) двухпроводной линии с заданной геометрией;
б) коаксиальной линии с заданной геометрией;
в) полосковой линии с заданной геометрией.
8. Что такое входное сопротивление линии? От чего оно зависит?
9. В каких случаях а) Z вх=0? б) Z вх=∞? в) Z вх=const по всей линии?
10. Что такое коэффициент отражения? От чего он зависит?
11. Что такое: а) фаза бегущей волны? б) волновое число? в) фазовая скорость? г) длина волны? Как связаны между собою эти величины?
12. Показать, что фазовая скорость бегущей волны в двухпроводной линии равна скорости света в вакууме.
13. Изобразить структуру электромагнитного поля в двухпроводной линии. Куда направлен вектор Пойнтинга в режиме бегущих волн? Почему волны в линии называются плоскими поперечными?
14. Что такое согласованная нагрузка?
15. Что такое режим стоячих волн и как его реализовать?
16. Что такое режим смешанных волн и как его реализовать?
17. Что такое резонансные отрезки линии? Записать входные сопротивления четверть- и полуволновых отрезков линии.
18. Согласованную нагрузку включили на расстоянии а =λ/4 от конца разомкнутой линии. Как изменится режим в линии? Показать распределение токов и напряжений в этом случае.
19. Выполнить задание предыдущего пункта для случая а =λ/2.
20. Одна согласованная нагрузка включена в конце линии, а другая где-то в середине. Какой режим будет в каждой части линии?
21. Что такое КСВ? Как он связан с коэффициентом отражения? Каков КСВ в разных режимах?
22. Как оценивается качество согласования нагрузки с линией?
23. Как выражается КСВ через сопротивление активной нагрузки?
24. Каков должен быть КСВ в линии, если допустимое отражение мощности от активной нагрузки равно 1%? Каково при этом допустимое отклонение R н от ρ?
ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ
Пусть размеры линии в её сечении (рис. 1): r =1.5 мм, d =82 мм; материал проводов – медь.
1. По формулам (18) вычислить погонные параметры линии L 0 (мкГн/м) и С 0 (пФ/м), а по формуле (19) – её волновое сопротивление ρ.
2. Воздушную линию можно считать без потерь, если её погонное сопротивление R 0≪ω L 0. С учётом скин-эффекта, погонное сопротивление цилиндрического провода радиусом r на частоте f оценивается по формуле
R 0= 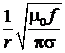 ,
,
где σ – проводимость материала провода; для меди σ = 0,5·108 (Ом·м)−1.
Оценить, выполняется ли условие R 0≪ω L 0 на частоте f =100 МГц (учесть, что проводов у линии – два).
ЛИТЕРАТУРА
1. Фейнман Р. Фейнмановские лекции по физике. – М.: Мир, 1977. – С. 221-226.
2. Бессонов Л. А. Теоретические основы электротехники. – М.: Высшая школа, 1973. – Гл. 12.
3. Зернов Н. В., Карпов В. Г. Теория радиотехнических цепей. − М.: Энергия, 1965. – Гл. 6.
*) Иногда, наряду с КСВ, используют и обратную ему величину – коэффициент бегущей волны (КБВ): КБВ=1/КСВ.