Задание для лабораторной работы № 2

Задание на лабораторную работу №1

1.Для набора данных, приведенных в Индивидуальном задании:

1.1.Рассчитайте коэффициент корреляции. Сделайте вывод о силе и направлении связи между переменными.

1.2.Постройте поле корреляции. Правильно ли сделан вывод о взаимосвязи между переменными в п. 1.1. Если нет, сделайте новый вывод.

Коэффициент корреляции рассчитываем по следующим формулам: . Линейный коэффициент корреляции находится в пределах: . Чем ближе абсолютное значение к единице, тем сильнее линейная связь между факторами. При имеем строгую функциональную зависимость. Если , то связь умеренная или средняя.

2.Определите, какая из переменных является фактором (причиной), а какая - результирующим показателем (следствием)?

– зависимая переменная или результативный признак (V капиталовложений); – независимая или признак – фактор (V выпуска продукции).

З. Постройте уравнение линейной регрессии, воспользовавшись формулами определения коэффициентов регрессии, приведенными в лекции (форм.5).

Уравнение линейной регрессии . Параметры a и b определяются по следующим

формулам: , , .

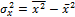4. Рассчитаны прогнозируемые значения результирующего показателя для каждого значения фактора Xj. Построено новое поле корреляции с линией регрессии по значениям .

5. Определите стандартную ошибку регрессии и коэффициент детерминации. Сделайте вывод, какая доля вариации результирующего показателя У объясняется с помощью уравнения регрессии.

Стандартная ошибка регрессии определяется по формуле и коэффициент детерминации . Доля вариации равна 83,3%.

6. Пользуясь построенным уравнением регрессии, ответьте на вопрос, заданный в Индивидуальном задании для выбранного набора данных.

При увеличении объема капиталовложений на 1 млн. руб. объем выпуска продукции в среднем

увеличивается на 1,403 млн. руб.

7. Используйте функцию ЛИНЕЙН для определения коэффициентов регрессии и других показателей регрессии. Проверьте ранее выполненные расчеты.

Задание для лабораторной работы № 2

1. Найти параметры уравнения линейной регрессии, дать экономическую интер­претацию коэффициента регрессии.

После проведенных расчетов линейная модель имеет вид: ŷ_х = 15,927+1,404x. Экономический смысл параметра регрессии заключается в следующем: с увеличением капиталовложений на 1 единицу выпуск продукции увеличивается на 1,404 единиц.

2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков s²; построить график остатков.

Вычисленные остатки приведены в таблице. Остаточная сумма квадратов составила 297,588. Дисперсия остатков составила 37,199.

4. Осуществить проверку значимости параметров уравнения регрессии с помо­щью t-критерия Стьюдента (а = 0,05).

5. Вычислить коэффициент детерминации, проверить значимость уравнения рег­рессии с помощью F - критерия Фишера (а = 0,05), найти среднюю относи­тельную ошибку аппроксимации. Сделать вывод о качестве модели.

F факт > F табл - это говорит о том, что уравнение регрессии статистически значимо. Средняя ошибка аппроксимации А = 4,2%. Это говорит о том, что качество уравнения регрессии хорошее. Расчетные значения отклоняются от фактических на 4,2%.

6. Осуществить прогнозирование среднего значения показателя У при уровне значимости а = 0,05 и а = 0,1, если прогнозное значения фактора Х составит 80% от его максимального значения.

7. Представить графически: фактические и модельные значения У, точки прогноза.

8. Все вычисления проверить через опцию «регрессия».

Контрольные вопросы для лабораторных работ №1, №2

1. Какими способами можно обнаружить наличие взаимосвязи между двумя переменными? Кратко охарактеризуйте каждый из них.

Наличие взаимосвязи между двумя переменными можно обнаружить 3 способами: графическим, аналитическим, экспериментальным. При изучении взаимосвязи между 2 переменными графический способ подбора вида уравнений основан на поле корреляции. Аналитический способ основан на изучении материальной природы связи исследуемых признаков(т.е. исходя из теории изучаемой связи).При эксперемт. способе перебираются разные математические функции в автоматическом режиме и из них выбирается та функция, у которой S ост. минимальна. Если же она оказывается примерно одинаковой для нескольких функций, то предпочтение отдается более простым функциям.

2. Как рассчитывается коэффициент корреляции? Как можно интерпретировать его значения?

Уравнение регрессии всегда дополняется коэффициентом корреляции или показателем тесноты связи, в качестве которого используется коэфф. корреляции .Величина коэффициента корреляции находится впределах от -1до 1. Величина лин. коэфф. корреляции оценивает тесноту связи признака X и Y в линейной модели.

3. Какие проблемы, содержащиеся в данных, могут привести в неверной интерпретации значения коэффициента корреляции?

Ошибка при интерпретации коэф. корреляции может быть допущена в том случае, когда в выборке присутствуют аномальные значения (очевидно большие или очевидно низкие). Они могут возникнуть из-за неоднородности исследуемых элементов выборки. Вторая проблема, содержащиеся в данных, которая может привести в неверной интерпретации значения коэффициента корреляции, это неправильный выбор той или иной функции для ŷ_х и недоучет в уравнении регрессии какого-либо существенного фактора, т.е. использование парной регрессии вместо множественной. И третья проблема связана с ошибками измерения.

4. Что представляет собой математическая модель взаимосвязи между экономическими переменными? Как называются переменные, входящие в ее состав? Какой характер может иметь взаимосвязь между этими переменными?

Математическая модель взаимосвязи между экономическими переменными представляет собой математическую функцию (спецификацию модели). Переменные, входящие в ее состав, - у (результативный признак, независимая переменная) и х (признак фактор, независимая переменная, объясняющая). Характер взаимосвязи между переменными определяется по полю корреляции. Он может быть линейным и нелинейным.

5. Дайте определение функции регрессии. Чем отличаются функция регрессии и регрессионная модель? Покажите на графике условное математическое ожидание результирующего показателя У при заданном значении х фактора Х. Покажите индивидуальное значение у (х).

Регрессия – величина, выражающая зависимость среднего значения случайной величины y от значения случайной величины x. Функция регрессии – это модель вида y=x, где у – зависимая переменная, а х – независимая. Регрессионная модель – экономически – статистическая модель, основанная на уравнении регрессии, связ-ем величины входных и выходных данных.

6. Назовите причины наличия в регрессионной модели случайного отклонения. Покажите случайное отклонение на графике.

Причины наличия в регрессионной модели случайного отклонения это – спецификация модели, выборочный характер исходных данных, особенности измерения переменных.

7. Какова основная задача регрессионного анализа? Назовите его основные этапы и кратко охарактеризуйте каждый.

Задача заключается в получении сведений о том, какую форму и характер имеет зависимость между исследуемыми переменными; установление формы зависимости, определение функции регрессии, оценка неизвестных значений зависимой переменной. Этапы: формулировка задачи, определение зависимых и независимы переменных, сбор статистических данных, формулировка гипотезы о форме связи, определение функции регрессии, оценка точности регрессионного анализа, интерпретация полученных результатов, предсказание неизвестных значений зависимой переменной.

8. В чем суть метода наименьших квадратов? Запишите уравнение линейной парной регрессии. Как рассчитывается прогнозируемое значение результирующего показателя? Покажите его на графике.

Суть МНК: позволяет получить такие оценки параметров a и b при которых сумма квадратов отклонения фактического значения результирующего признака у от ŷ_х минимально. .

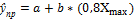
9. Как рассчитываются коэффициенты регрессии с помощью метода наименьших квадратов? Что показывает каждый из этих коэффициентов?

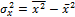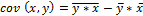, , , . величина параметра b показывает среднее изменение результирующего с изменением фактора на 1 единицу. Формально – значение при 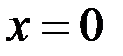. Дисперсия – характеристика случайной величины, определяется как математическое ожидание квадрата отклонения случайной величины от её математического ожидания. Ковариация – числовая характеристика совместного распределения 2-х случайных величин равная математическому ожиданию произведения отклонений этих случайных величин от их математического ожидания.

10. Какие характеристики 'используются для оценки точности предсказаний по уравнению регрессии? Опишите каждую из них.

Коэффициент детерминации - характеризует долю дисперсии результативного признака у; для оценки качества подбора. Средняя ошибка аппроксимации - , оценивает качество модели из относительных отклонений по каждому наблюдению. Критерий Фишера - , с его помощью определяется статистическая значимость уравнения регрессии. Критерий Стьюдента - 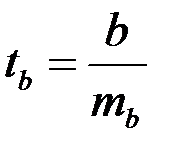, с его помощью оценивается значимость параметров уравнения.

11. Покажите на графике общий разброс значений результирующего показателя относительно среднего значений и две его составляющие. Какие показатели являются мерой каждого из видов разброса? Как они связаны с коэффициентом детерминации?

12. Для чего используется функция ЛИНЕЙН? ЧТО определяют ее аргументы «константа» и «статистика»?

Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива. Уравнение для прямой линии имеет следующий вид: y = mx + b или

y = m1x1 + m2x2 +... + b (в случае нескольких диапазонов значений x), где зависимое значение y — функция независимого значения x, значения m — коэффициенты, соответствующие каждой независимой переменной x, а b — постоянная. Y, x и m могут быть векторами. Функция ЛИНЕЙН возвращает массив {mn;mn-1;...;m1;b}. Функция ЛИНЕЙН может также возвращать дополнительную регрессионную статистику.

· Конст. Необязательный аргумент. Логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.

· Если аргумент конст имеет значение ИСТИНА или опущен, то константа b вычисляется обычным образом.

· Если аргумент конст имеет значение ЛОЖЬ, то значение b полагается равным 0 и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.

· Статистика. Необязательный аргумент. Логическое значение, которое указывает, требуется ли возвратить дополнительную регрессионную статистику.

· Если аргумент статистика имеет значение ИСТИНА, функция ЛИНЕЙН возвращает дополнительную регрессионную статистику. Возвращаемый массив будет иметь следующий вид: {mn;mn-1;...;m1;b:sen;sen-1;...;se1;seb:r2;sey:F;df:ssreg;ssresid}.

· Если аргумент статистика имеет значение ЛОЖЬ или опущен, функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.

Кроме того, на защите лабораторной работы студент должен по указанию преподавателя выполнить следующие действия:

1. Указать в массиве результатов функции ЛИНЕЙН значения известных ему показателей.

2. Дать интерпретацию заданного значения коэффициента корреляции.

З. Рассчитать на основании заданной функции регрессии прогнозируемое значение результирующего показателя, соответствующее заданному значению фактора.

4. Дать интерпретацию заданного значения коэффициента детерминации.