ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Нейроподобная сеть
Нейроподобная сеть представляет собой совокупность нейроподобных элементов определенным образом связанных между собой и внешней средой. Входной вектор (кодирующее входное воздействие или образ внешней среды) подается на сеть путем активации входных нейроподобных элементов. Множество выходных сигналов y1, … yk называют вектором выходной активности или паттерном активности нейронной сети. Веса связей нейронов сети удобно представлять в виде матрицы W, где wij вес связи между i-м и j-м нейронами. В процессе функционирования (эволюция состояния) сети осуществляется преобразование входного вектора в выходной, т.е. некоторая переработка информации, которую можно интерпретировать, как функцию гетеро- или автоассоциативной памяти. Конкретный вид выполняемого сетью преобразования информации, обуславливается не только характеристиками нейроподобных элементов, но и особенностями ее архитектуры, т.е. той или иной топологией межнейронных связей, выбором определенных подмножеств входных и выходных нейронов, и т.д.
Рассмотрим ряд свойств нейронных сетей:
1. Нейросети принимают решения на основе «самостоятельно» приобретаемого опыта. В данном случае это означает то, что создателю экспертной системы не требуется устанавливать взаимосвязи между входными данными и необходимым решением, тратя время на разнообразную статобработку, подбор математического аппарата, создание и проверку математических моделей.
2. Решение принимаемое нейросетью не является категоричным. Сеть выдает решение вместе со степенью уверенности в нем, что позволяет пользователю критически оценивать результат.
3. Нейросеть позволяет моделировать ситуацию принятия решения, что позволяет посмотреть, «а что будет если»
4. Нейросеть дает ответ очень быстро (доли секунды), что позволяет их использовать их в динамических системах, требующих незамедлительного принятия решения.
5. Возможности нейросетей (коррекция классификационной модели, минимизация параметров) позволяет упрощать процесс создания экспертных систем, определять направления научного поиска.[2]
По типам связей нейронные сети можно классифицировать на многослойные, «каждый с каждым», с прямыми и симметричными связями, сети с латеральным торможением и комбинированные из этих типов сети.
По способу создания нейронные сети можно разделить на обучаемые и формируемые нейронные сети, а также смешанные.
Обучение нейроподобной сети.
Одно из основных свойств нейроподобной сети – способность к самоорганизации, самоадаптации с целью улучшения качества функционирования. Это достигается обучением сети, алгоритм которого задается набором обучающих правил.
Процесс обучения представляет собой автоматический поиск закономерности между совокупностью обучающих данных и заранее известными результатами. Если представить выходную информацию в виде метрического пространства, то в процессе обучения расстояния между выходными образами различных классов будет увеличиваться, а для одного класса будут сокращаться и стремиться к той точке пространства, в которой этот класс определен.
В процессе обучения могут возникнуть ситуации, при которых обучение прекращается до того как сеть будет полностью обучена. Это возможно, например, в случае, когда входные образы имеют одинаковые параметры, но при этом принадлежат к различным классам и сеть не может найти признака, по которому их можно разделить. Поэтому до обучения очень важно задать правильную классификацию, иначе в процессе обучения модель придется менять. Например, образы относятся к трем классам, а сеть сконфигурирована лишь для двух. В этом случае процесс обучения не будет закончен и модель сети придется менять.
Алгоритмы обучения на основе обратного распространения ошибки.
Простейший способ обучения – по очереди менять каждый весовой коэффициент сети (далее просто - вес связи) таким образом, чтобы оптимизировался какой-либо критерий качества работы сети (обычно – среднеквадратичное отклонение выходного сигнала сети от требуемого значения). Понятно, что такой способ малоэффективен. Выгоднее вычислить совокупность производных ошибки сети по весовым коэффициентам – градиент ошибки по весам связей – и изменить все веса сразу на величину, пропорциональную соответствующей производной. Один из возможных методов, позволяющих вычислить градиент ошибки – алгоритм обратного распространения.
Модель нейрона для алгоритма обратного распространения.
В данной работе использовалась следующая модель нейрона, позволяющая применить алгоритм обратного распространения к сетям с широким набором различных свойств и топологий.
Входные данные D поступают на входы связей нейрона, где происходит их взвешивание:
X = f (W,D), (1)
где W – весовой коэффициент или набор коэффициентов (как правило, f(W,D) = W*D).
Далее сигналы X с выходов связей поступают на вход нейрона и суммируются:
Xсум = S Xвхi, (2)
i=1,n
после чего подаются на нелинейный элемент (он может быть как встроенный, так и задаваемый пользователем):
Y = f (Xсум + С). (3)
Сигнал Y затем рассылается по всем связям, выходящим из данного нейрона, после чего процесс повторяется заданное количество раз, пока на выходе сети не появятся требуемые данные.
Нейроны и связи выполнены в виде отдельных объектов, связанных между собой только функциями передачи данных, и допускают их независимую модификацию. Помимо этого, предусмотрена возможность задания произвольной внешней переходной функции нейрона.
Классический алгоритм обратного распространения.
Для начала предположим, что имеется послойно организованная сеть, в которой каждый нейрон предыдущего слоя соединен с каждым нейроном последующего. Будем индексировать символом «j» нейроны текущего слоя, и «i» - предыдущего. Будем также считать, что используется сигмоидальная функция активации нейрона, а в качестве критерия оптимизации используется среднеквадратическое отклонение наблюдаемого выхода сети от требуемого. В этом случае алгоритм обратного распространения состоит из четырех шагов:
1) подать на вход сети входной вектор Х и получить выходной вектор Y=(Yj(n))
2) Вычислить ошибку на выходе сети E(n)=Sej(n)2, где ej(n)=Dj-Yj(n)
3) Определить ошибки скрытых слоев:
Эту процедуру можно повторять, чтобы вычислять E стольких предыдущих слоев, сколько их есть.
 |
4) Вычислить коррекцию настраиваемых параметров. Например, на основе анализа градиента функции ошибок по настраиваемым параметрам
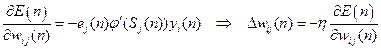
5) Проверить уровень выходной ошибки сети. Если ошибка ниже заданного порога, то закончить обучение, иначе к п.1
Схема сети приведена на Рис.1.

Рис.1. Обратное распространение ошибки. Модель многослойной сети.
Архитектура «многослойный перцептрон».
Обучение с учителем.
Обучение – коррекция по ошибке (обратное распространение ошибки).
Число слоев k.
Слой 0 – рецептивный, слои 1- k – нелинейные нейроны.
Число входов n, число выходов р.
Сеть прямого распространения.
ПРАКТИЧЕСКАЯ ЧАСТЬ