Принимая, что сжатие природного газа происходит по адиабате (k=1,31), находим температуру нагнетания по формуле:
 (2.16)
(2.16)


2.6.Выбор клапанов по пропускной способности
Допустимую относительную потерю мощности в клапанах  выбираем по рекомендациям из таблице 2.6.
выбираем по рекомендациям из таблице 2.6.
где  - суммарные потери мощности в нагнетательных и всасывающих клапанах,
- суммарные потери мощности в нагнетательных и всасывающих клапанах,  - номинальная индикаторная мощность ступени.
- номинальная индикаторная мощность ступени.
Таблица 2.6
| Параметр клапана | Давление всасывания, МПа | ||||
| 0,1-0,5 | 0,5-1,5 | 1,5-5 | 5-15 | 15-50 | |
( )max,%
Fвсmax )max,%
Fвсmax
| 11,2 0,22 | 9,2 0,2 | 7,4 0,18 | 5,8 0,16 | 4,4 0,14 |
Скорость звука при условиях в клапане определяем по формуле:
 (2.17)
(2.17)
где R – газовая постоянная природного газа; R= 505 Дж/(кг·К) – берется из справочных данных.
Рассчитаем скорость звука в первой ступени:

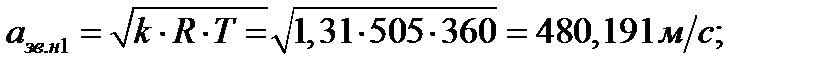
Рассчитаем скорость звука во второй ступени:


Допустимая условная скорость газа в клапане:
 (2.18)
(2.18)
Для первой ступени:


Для второй ступени:


Выберем число клапанов: zкл.вс1 = 3, zкл.вс2 = 2, zкл.н1 = 3, zкл.н2 = 2
Определяем необходимое значение эквивалентной площади клапана, которая обеспечит работу компрессора с допустимыми потерями мощности в клапанах. Значение необходимой эквивалентной площади Ф считаем по формуле:
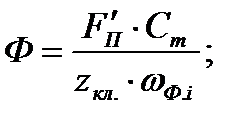 (2.20)
(2.20)
где  –площадь поршня;
–площадь поршня;  – средняя скорость поршня;
– средняя скорость поршня;  – число всасывающих или нагнетательных клапанов в полости цилиндра.
– число всасывающих или нагнетательных клапанов в полости цилиндра.




По необходимым значениям эквивалентной площади клапанов подбираем стандартизованные клапаны типа.
Основные данные клапанов занесем в таблицу 2.7:
Таблица 2.7
| Неполный шифр клапана | Эквивалентная площадь Ф, см², не менее | Мертвый объем клапана Vм, см³ | Ширина прохода в седле b, мм | Высота подъема пластины h, мм | d1, мм | d2, мм | hBC = hH, мм | h1, мм | H, мм | Число кольцевых проходов |
| I ступень | ||||||||||
| ВКТ 100 - 2,0 - 6,4 | 8,8 | |||||||||
| НКТ 110 - 1,5 - 4,0 | 7,5 | 1,5 | ||||||||
| II ступень | ||||||||||
| ВКТ 100 - 1,5 - 1,0 | 6,9 | 1,5 | ||||||||
| НКТ 100 - 1,5 - 4,0 | 6,9 | 1,5 |
2.7.Подбор пружин клапанов
Найдем скорректированное значение эквивалентной скорости газа в клапане:
 .
.
Подставим значения:




Скорректируем значение критерия скорости газа в клапане:
 .
.
Подставим значения:
 ;
;  ;
;
 ;
;  .
.
По известному скорректированному значению критерия скорости Fi находим максимальное значение потери давления в клапане в теоретическом хmaxi случае. Для этого воспользуемся графиком [4] зависимости хmaxi от Fi:

Рисунок 2.1– Зависимость  от F:
от F:
x max вс1 = 0,05; x max вс2 = 0,04; x max н1 = 0,058; x max н2 = 0,06.
Задаемся отношением:  (принимаем Θ = 0,15).
(принимаем Θ = 0,15).
По известным значениям Θ и хmaxi найдем минимальное значение перепада давлений в клапане, необходимого для преодоления силы упругости пружины в полностью открытом клапане. Для этого воспользуемся формулой
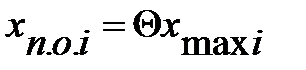 .
.
Подставим значения
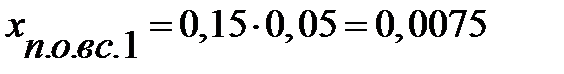 ;
;  ;
;
 ;
;  .
.
Рассчитаем минимальный перепад давлений необходимый для полного открытия клапана по формуле:
 ,
,
где pi – давления всасывания и нагнетания в I и II ступени.
Подставим значения
 Н/м2;
Н/м2;  Н/м2;
Н/м2;
 Н/м2;
Н/м2;  Н/м2.
Н/м2.
Находим отношение полной высоты подъема пластины к ширине прохода в щели. Значения h и b берем из табл. 2.7:
I ступень Всасывающие клапаны:  ;
;
Нагнетательные клапаны: 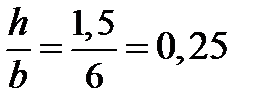 .
.
II ступень Всасывающие клапаны: 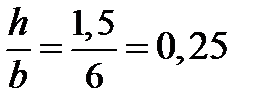 ;
;
Нагнетательные клапаны: 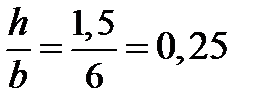 .
.
На основании полученных значений отношений h / b находим коэффициент давления потока ρр. Для этого воспользуемся графиком коэффициента давления потока для кольцевых и дисковых клапанов:

Рисунок 2.2 –Коэффициент давления потока для кольцевых и дисковых клапанов
ρ р.вс1 = 1,24; ρ р.вс2 = 1,2; ρ р.н1 = 1,2; ρ р.н2 = 1,2
Рассчитаем приведенную силу упругости пружины по формуле:
 .
.
Все необходимые значения известны, подставим их в приведённую формулу и получим
 Н/м2;
Н/м2; 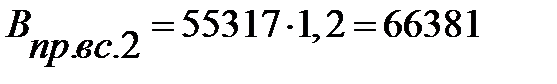 Н/м2;
Н/м2;
 Н/м2;
Н/м2;  Н/м2.
Н/м2.
Округляем значения приведенной силы упругости пружины до ближайшего номинального значения из стандартного ряда:
 Н/м2;
Н/м2;  Н/м2;
Н/м2;
 Н/м2;
Н/м2;  Н/м2.
Н/м2.
Рассчитаем силу давления пружины на пластины клапана по формуле
 ,
,
где fc – площадь проходного сечения в седле, она определяется по формуле:
 .
.
Значения Фi берем из табл.2.7 тогда:
 см2;
см2;  см2;
см2;
 см2;
см2;  см2.
см2.
и
 Н;
Н;
 Н;
Н;
 Н;
Н;
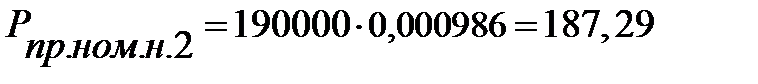 Н.
Н.
Полученные значения занесем в общую таблицу 2.8.
Таблица 2.8
| № | Параметр | I ступень | II ступень | ||
| всасывание | нагнетание | всасывание | нагнетание | ||
| Число цилиндров | |||||
| Диаметр цилиндров Di,м | 0,210 | 0,16 | |||
| Площадь поршня F'Пi, м2 | 0,035 | 0,020 | |||
| Объем описываемый поршнем Vhi, м3/с | 0,493 | 0,286 | |||
| Температура Т, К | 348,55 | 359,64 | |||
| Давление Р, Мпа | 9,22 | 9,22 | |||
| Число клапанов z | |||||
| Коэффициент подачи λ | 0,904 | 0,933 | |||
| Индикаторная мощность Nui, кВт | |||||
| Индикаторная мощность компрессора Nu, кВт | |||||
| Частота вращения коленчатого вала n0, с-1 | 16,667 | ||||
| Мощность двигателя Nд, кВт | 3897,82 |
3. Динамический расчет
3.1. Уравновешивание компрессора
Механизм движения компрессора – коленчатый вал, шатун, поршень. Из них поршень, совершает только возвратно-поступательные движения, коленчатый вал – вращательное, шатун – сложно-плоское, которое можно рассматривать как результат сложения двух движений: возвратно-поступательного вместе с поршнем и вращательного вместе с коленчатым валом. В связи с этим массу шатуна разбивают на две части:  и
и 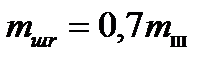 .
.
Таблица 3.1 - Масса элементов кривошипно-шатунного механизма, кг
| Элемент кривошипно-шатунного механизма | Масса |
| Поршень m п, кг | |
| Шатун m ш, кг | |
| Коленчатый вал m к, кг | |
| Крейцкопф с крейцкопфным пальцем m кр,кг | |
| Шток m шт |
 кг
кг
 кг
кг
Масса возвратно-поступательно движущихся частей будет определяться по формуле:
 .
.
Масса вращающихся частей составит:

 (3.1)
(3.1)
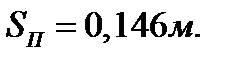
где S – ход поршня.
Остальные величины, необходимые для расчета, составляют:
радиус кривошипа, м,  , где S = 0,146 м – ход поршня;
, где S = 0,146 м – ход поршня;
угловая скорость вращения вала, рад/с,  ;
;
Исходя из чертежа, lш = 0,379, где lш – длина шатуна.

Рисунок 3.1–Схема уравновешивания поршневого компрессора
l= 1500мм, l’= 1600 мм
Уравновешивание вращающихся масс
Так как компрессор оппозитный, то при такой компоновке силы инерции вращающихся масс уравновешены, так как эти массы обычно одинаковы для обоих рядов. Момент сил инерции Ir может быть легко уравновешен моментом сил инерции противовесов, установленных на валу. Масса противовеса:
mпр=mr· l/l’ =84*1500/1600=360кг.
Силы инерции соответственно в первом и втором ряду:

3.2. Построение индикаторной диаграммы
Схематизированные индикаторные диаграммы строятся в координатах усилие – ход поршня. Сначала на диаграммы наносятся средние усилия всасывания Pг.вс и нагнетания Pг.н, которые находим по формулам
 кН,
кН,
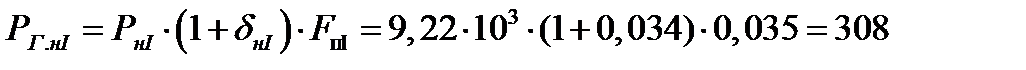 кН,
кН,
 кН,
кН,
 кН,
кН,
Линию сжатия строим в соответствии с уравнением политропы сжатия
 ,
,
где Pг1, S1 – координаты точки, соответствующей началу сжатия; Pгi, Si - текущие координаты;  ,
,  и показатели политропы сжатия для первой и второй ступени соответственно.
и показатели политропы сжатия для первой и второй ступени соответственно.
Линию расширения строят аналогично, пользуясь уравнением политропы расширения:
 ,
,
где Pг3, S3 – координаты точки, соответствующей началу обратного расширения; Pгj, Sj – текущие координаты; 
 -показатели политропы расширения для первой и второй ступени соответственно.
-показатели политропы расширения для первой и второй ступени соответственно.
Другие точки рассчитываются аналогично. В связи с этим остальные расчеты представим в виде таблиц результатов 3.2 – 3.3:
Кривые сжатия и расширения строятся до пересечения с линиями средних усилий нагнетания Pг.н и всасывания Pг.вс соответственно.
Таблица 3.2 - Расчет политропы расширения и сжатия для I ступени
| Sc 1, мм | Р Г1, кН | Sр 1, мм | Р Г1, кН |
Таблица 3.3 - Расчет политропы расширения и сжатия для II ступени
| Sc 1, мм | Р Г1, кН | Sр 1, мм | Р Г1, кН |
Для проверки правильности построения индикаторных диаграмм определим индикаторную мощность, кВт, и сравним ее с индикаторной мощностью, полученной в результате теплового расчета:
 ,
,
где Pи – среднеиндикаторная поршневая сила, действующая в ряду поршневого компрессора, кН; S – ход поршня, мм; n – частота вращения вала компрессора, об/с; z – число цилиндров.
Учитывая, что в нашем случае индикаторные диаграммы обеих полостей в каждом ряду различаются, получим

где mp = 0,5 кН/мм - масштабный коэффициент газовой силы; ms = 0,5 мм/мм -масштабный коэффициент хода поршня; fi – площадь соответствующей индикаторной диаграммы одной полости цилиндра, мм2.
После построения диаграмм подсчитаем их площади: f1 = 16500 мм2, f2 = 17300 мм2.
Тогда:
 кН;
кН;
 кН;
кН;
А индикаторная мощность по ступеням будет иметь следующие величины:
 кВт;
кВт;
 кВт;
кВт;
При выполнении термодинамического расчета были получены следующие значения:
 кВт;
кВт; 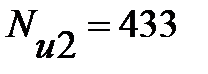 кВт
кВт
Погрешность составляет около 3,7 %.
Результаты хорошо согласуются, следовательно, построение индикаторных диаграмм выполнено правильно.

Рисунок 3.2–Индикаторные диаграммы 1-й и 2-й ступени.
3.3. Построение диаграмм суммарной поршневой силы
Суммарная сила РΣ направленная вдоль оси цилиндра определяется по формуле:

где Рг - газовая сила со стороны вала, кН; Ргк- газовая сила со стороны крышки, кН
Ir – сила инерции поступательно движущихся масс, кН;
Ртр – сила трения в поступательно движущихся парах, кН.
Выполним построение диаграмм поршневых сил. По оси ординат будем откладывать усилия вдоль оси ряда Р, а по оси абсцисс — угол поворота коленчатого вала α. При перенесении усилий с индикаторных диаграмм на силовую диаграмму учтем поправку Брикса  , введение которой приводит в соответствие углы поворота коленчатого вала и перемещения поршня. На силовую диаграмму наносим также силу инерции возвратно-поступательно движущихся масс и силу трения в цилиндропоршневой группе.
, введение которой приводит в соответствие углы поворота коленчатого вала и перемещения поршня. На силовую диаграмму наносим также силу инерции возвратно-поступательно движущихся масс и силу трения в цилиндропоршневой группе.
Силу трения Pтр в рядах полагают постоянной по модулю и меняющую знак в мертвых точках. Для её расчета воспользуемся формулой:

где Nи – индикаторная мощность, кВт; ηмех = 0,9 – механический КПД.
После нанесения на диаграмму всех сил, действующих в данном ряду компрессора, проводим их графическое суммирование, и получаем график суммарной поршневой силы PΣ.
 кН;
кН;
 кН.
кН.
Расчет сил сведен в табл. 3.4 и 3.5, а диаграмма представлена
на рис. 3.3-3.4
Таблица 3.4 - Результаты расчетов для построения диаграммы суммарной силы, действующей в ряду I ступени
| α, ° | Рг, кН | Ртр, кН | Is, кН | Ргк, кН | РΣ, кН |
| -5,337 | 129,711 | -85 | |||
| -5,337 | 123,199 | -88 | |||
| -5,337 | 104,665 | -95 | |||
| -5,337 | 76,907 | -108 | |||
| -5,337 | 43,907 | -130 | -6 | ||
| -5,337 | 10,007 | -154 | -64 | ||
| -5,337 | -20,949 | -154 | -95 | ||
| -5,337 | -46,292 | -154 | -121 | ||
| -5,337 | -64,856 | -154 | -139 | ||
| -5,337 | -76,907 | -154 | -151 | ||
| -5,337 | -83,716 | -154 | -158 | ||
| -5,337 | -86,914 | -154 | -161 | ||
| -87,813 | -154 | -157 | |||
| 5,337 | -86,914 | -85 | -80 | ||
| 5,337 | -83,716 | -85 | -72 | ||
| 5,337 | -76,907 | -85 | -56 | ||
| 5,337 | -64,856 | -85 | -29 | ||
| 5,337 | -46,292 | -85 | |||
| 5,337 | -20,949 | -85 | |||
| 5,337 | 10,007 | -85 | |||
| 5,337 | 43,907 | -85 | |||
| 5,337 | 76,907 | -85 | |||
| 5,337 | 104,665 | -85 | |||
| 5,337 | 123,199 | -85 | |||
| 5,337 | 129,711 | -85 |
Таблица 3.5 - Результаты расчетов для построения диаграммы суммарной силы, действующей в ряду II ступени
| α, ° | Рг, кН | Ртр, кН | Is, кН | Ргк, кН | РΣ, кН |
| -5,753 | 129,711 | -92 | |||
| -5,753 | 123,199 | -94 | |||
| -5,753 | 104,665 | -101 | |||
| -5,753 | 76,907 | -116 | |||
| -5,753 | 43,907 | -140 | -10 | ||
| -5,753 | 10,007 | -166 | -70 | ||
| -5,753 | -20,949 | -166 | -101 | ||
| -5,753 | -46,292 | -166 | -127 | ||
| -5,753 | -64,856 | -166 | -145 | ||
| -5,753 | -76,907 | -166 | -157 | ||
| -5,753 | -83,716 | -166 | -164 | ||
| -5,753 | -86,914 | -166 | -167 | ||
| -87,813 | -166 | -162 | |||
| 5,753 | -86,914 | -97 | -85 | ||
| 5,753 | -83,716 | -92 | -73 | ||
| 5,753 | -76,907 | -92 | -55 | ||
| 5,753 | -64,856 | -92 | -26 | ||
| 5,753 | -46,292 | -92 | |||
| 5,753 | -20,949 | -92 | |||
| 5,753 | 10,007 | -92 | |||
| 5,753 | 43,907 | -92 | |||
| 5,753 | 76,907 | -92 | |||
| 5,753 | 104,665 | -92 | |||
| 5,753 | 123,199 | -92 | |||
| 5,753 | 129,711 | -92 |

Рисунок 3.3–Диаграмма суммарной поршневой силы, действующей в ряду I ступени.

Рисунок 3.4–Диаграмма суммарной поршневой силы, действующей в ряду II ступени.
Нормальные силы, действующие на стенки цилиндра:
 где β - угол между осями цилиндра и шатуна определяется по формуле
где β - угол между осями цилиндра и шатуна определяется по формуле 
Усилия по шатуну определяются по формуле:

Тангенциальные усилия на кривошип:

Радиальные усилия на кривошип:

Результаты расчетов сил Рш, N, Pr и Pt приведены в табл. 3.6 и 3.7.
Усилия на шатунную шейку вала рассчитываем по формуле:
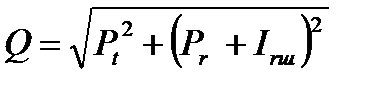
где Irш – центробежная сила от вращающейся части шатуна. Она определяется следующим образом:
 кН
кН
Таблица 3.6 - Результаты расчетов усилий, действующих в ряду I ступени
| α | β | N, кН | Рш, кН | Pt, кН | Pr, кН | Q, кН |
| 193,37 | 0,00 | 193,37 | ||||
| 0,05 | 5,76 | 115,51 | 35,42 | 109,94 | ||
| 0,10 | 8,69 | 90,25 | 52,44 | 73,45 | ||
| 0,14 | 6,68 | 49,03 | 39,07 | 29,62 | ||
| 0,17 | -1,09 | -6,52 | -6,11 | -2,27 | ||
| 0,19 | -12,18 | -65,47 | -65,29 | -4,88 | ||
| 0,19 | -18,70 | -97,10 | -95,29 | 18,70 | ||
| 0,19 | -22,84 | -122,77 | -110,61 | 53,28 | ||
| 0,17 | -23,55 | -141,17 | -108,77 | 89,99 | ||
| 0,14 | -20,79 | -152,67 | -92,24 | 121,65 | ||
| 0,10 | -15,29 | -158,79 | -65,78 | 144,52 | ||
| 0,05 | -8,05 | -161,45 | -33,96 | 157,84 | ||
| -156,81 | 156,81 | |||||
| -0,05 | 4,00 | -80,18 | 16,86 | 78,38 | ||
| -0,10 | 7,00 | -72,72 | 30,12 | 66,18 | ||
| -0,14 | 7,71 | -56,60 | 34,20 | 45,10 | ||
| -0,17 | 4,91 | -29,43 | 22,68 | 18,76 | ||
| -0,19 | -2,66 | 14,29 | -12,88 | -6,20 | ||
| -0,19 | -10,48 | 54,41 | -53,39 | -10,48 | ||
| -0,19 | -15,97 | 85,84 | -85,60 | 6,40 | ||
| -0,17 | -20,00 | 119,92 | -112,40 | 41,80 | ||
| -0,14 | -20,79 | 152,67 | -121,65 | 92,24 | ||
| -0,10 | -17,32 | 179,84 | -104,50 | 146,36 | ||
| -0,05 | -9,86 | 197,78 | -60,65 | 188,25 | ||
| 204,05 | 204,05 |
Таблица 3.7 - Результаты расчетов усилий, действующих в ряду II ступени
| α | β | N, кН | Рш, кН | Pt, кН | Pr, кН | Q, кН |
| 198,46 | 0,00 | 198,46 | ||||
| 0,05 | 5,74 | 115,17 | 35,32 | 109,62 | ||
| 0,10 | 8,60 | 89,35 | 51,92 | 72,72 | ||
| 0,14 | 6,42 | 47,16 | 37,58 | 28,50 | ||
| 0,17 | -1,76 | -10,56 | -9,90 | -3,68 | ||
| 0,19 | -13,30 | -71,49 | -71,30 | -5,33 | ||
| 0,19 | -19,86 | -103,13 | -101,20 | 19,86 | ||
| 0,19 | -23,96 | -128,79 | -116,03 | 55,90 | ||
| 0,17 | -24,55 | -147,17 | -113,39 | 93,81 | ||
| 0,14 | -21,61 | -158,64 | -95,85 | 126,41 | ||
| 0,10 | -15,87 | -164,74 | -68,25 | 149,93 | ||
| 0,05 | -8,34 | -167,38 | -35,21 | 163,63 | ||
| 0,00 | -162,31 | 0,00 | 162,31 | |||
| -0,05 | 4,23 | -84,76 | 17,83 | 82,86 | ||
| -0,10 | 7,03 | -73,00 | 30,24 | 66,44 | ||
| -0,14 | 7,54 | -55,34 | 33,44 | 44,10 | ||
| -0,17 | 4,44 | -26,59 | 20,49 | 16,95 | ||
| -0,19 | -3,53 | 18,97 | -17,09 | -8,23 | ||
| -0,19 | -11,64 | 60,44 | -59,30 | -11,64 | ||
| -0,19 | -17,09 | 91,86 | -91,61 | 6,85 | ||
| -0,17 | -21,01 | 125,92 | -118,03 | 43,89 | ||
| -0,14 | -21,61 | 158,64 | -126,41 | 95,85 | ||
| -0,10 | -17,89 | 185,78 | -107,95 | 151,20 | ||
| -0,05 | -10,16 | 203,71 | -62,47 | 193,89 | ||
| 209,96 | 209,96 |

Рисунок 3.5–Векторная диаграмма сил, действующих на шейку вала I (слева) и II (справа) ступени
3.4. Построение диаграмм суммарного противодействующего момента
Противодействующий момент, Нм, вызванный силами, действующими в ряду, обозначим Мi, найдем его по формуле:
 .
.
Расчет моментов для каждого ряда М1 и М2 представлен в виде табл. 3.8. При построении суммарного противодействующего момента МΣ = М1 + М2 следует учесть смещение моментов, возникающих в каждом ряду от действия поршневых сил, на угол, соответствующий развалу цилиндров. Угол развала между цилиндрами составляет 120º. Построение противодействующего момента М2 следует выполнять, начиная с точки, соответствующей α = 180º.
Дополнительно следует учесть момент сил трения вращательного движения:

где Nинд. – индикаторная мощность компрессора, рассчитанная при построении индикаторной диаграммы.

Опустим ось абсцисс диаграммы на величину, соответствующую Мтрr. По диаграмме суммарного противодействующего момента определим значение среднего момента Мср и нанесем его на эту диаграмму.
Расчет противодействующего момента МΣ сведен в таблицу 3.8, а диаграмма показана на рис. 3.6.
Величина Мср пропорциональна потребляемой компрессором мощности
Nк = ω·Мср,
где Мср = 17,39кНм, тогда
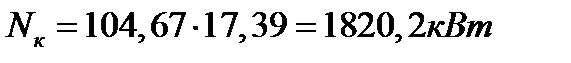 .
.
Из теплового расчета Nк = 2·1820,2 = 3640,4 кВт. Погрешность составляет 3,6 %, можно считать построения достаточно точными.
Таблица 3.8 - К расчету противодействующего момента
| α | М1, кНм | М2, кНм | М3, кНм | М4, кНм | М5, кНм | М6, кНм | МΣ, кНм |
| 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 2,586 | 2,586 | 2,586 | 2,578 | 2,578 | 2,578 | 15,491 | |
| 3,828 | 3,828 | 3,828 | 3,790 | 3,790 | 3,790 | 22,855 | |
| 2,852 | 2,852 | 2,852 | 2,743 | 2,743 | 2,743 | 16,785 | |
| -0,446 | -0,446 | -0,446 | -0,723 | -0,723 | -0,723 | -3,507 | |
| -4,766 | -4,766 | -4,766 | -5,205 | -5,205 | -5,205 | -29,912 | |
| -6,956 | -6,956 | -6,956 | -7,388 | -7,388 | -7,388 | -43,031 | |
| -8,074 | -8,074 | -8,074 | -8,470 | -8,470 | -8,470 | -49,634 | |
| -7,940 | -7,940 | -7,940 | -8,278 | -8,278 | -8,278 | -48,654 | |
| -6,734 | -6,734 | -6,734 | -6,997 | -6,997 | -6,997 | -41,192 | |
| -4,802 | -4,802 | -4,802 | -4,982 | -4,982 | -4,982 | -29,352 | |
| -2,479 | -2,479 | -2,479 | -2,570 | -2,570 | -2,570 | -15,148 | |
| 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| 1,231 | 1,231 | 1,231 | 1,302 | 1,302 | 1,302 | 7,598 | |
| 2,199 | 2,199 | 2,199 | 2,208 | 2,208 | 2,208 | 13,221 | |
| 2,496 | 2,496 | 2,496 | 2,441 | 2,441 | 2,441 | 14,812 | |
| 1,655 | 1,655 | 1,655 | 1,496 | 1,496 | 1,496 | 9,454 | |
| -0,940 | -0,940 | -0,940 | -1,248 | -1,248 | -1,248 | -6,563 | |
| -3,897 | -3,897 | -3,897 | -4,329 | -4,329 | -4,329 | -24,680 | |
| -6,249 | -6,249 | -6,249 | -6,687 | -6,687 | -6,687 | -38,810 | |
| -8,205 | -8,205 | -8,205 | -8,616 | -8,616 | -8,616 | -50,465 | |
| -8,880 | -8,880 | -8,880 | -9,228 | -9,228 | -9,228 | -54,324 | |
| -7,629 | -7,629 | -7,629 | -7,881 | -7,881 | -7,881 | -46,528 | |
| -4,427 | -4,427 | -4,427 | -4,560 | -4,560 | -4,560 | -26,962 | |
| 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |

Рисунок 3.6 – Диаграмма суммарного противодействующего момента
Планиметрированием найдем площадки, образованные кривой МΣ и прямой Мср. Общая высота этой диаграммы определяет предельное изменение кинетической энергии маховика на протяжении одного оборота коленчатого вала.
Определим требуемый момент инерции маховика:
 ,
,
где |ΔL| - абсолютное значение изменения энергии маховика за один оборот вала;
δ = 1/80 – степень неравномерности движения для асинхронного электродвигателя.

где μE – масштабный коэффициент диаграммы

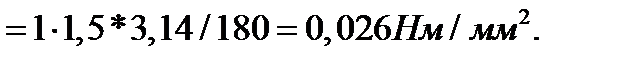
Абсолютное значение изменения энергии маховика за один оборот вала:

Момент инерции маховика

Как видно, требуемый момент инерции маховика меньше момента инерции электродвигателя. Следовательно, установка маховика не требуется.
Заключение
В результате выполнения расчетно-графической работы спроектирован оппозитный поршневой компрессор двойного действия производительностью 26,3 м3/мин.
Число ступеней – 2. Диаметр цилиндра I-й ступени – 210 мм,
II-й – 160 мм.
Давление всасывания – 5 МПа, нагнетания – 17 МПа. Клапаны – Кольцевые.
Список литературы
1. Юша, В. Л. Теория, расчёт и конструирование поршневых компрессоров: учебное пособие по курсовому проектированию / В.Л. Юша. – Омск: Изд-во ОмГТУ, 2006. – 120 с.
2. Френкель, М. И. Поршневые компрессоры: Теория, конструкции и основы проектирования / М. И. Френкель, 1969. - 743 с.
3. Пластинин, П. И. П